1 Análisis exploratorio de datos

Escuchando a los números :)

1.1 Análisis numérico, La voz de los números

“La voz de los números” – una metáfora de Eduardo Galeano. Escritor y novelista.

Los datos que exploramos podrían ser como jeroglíficos egipcios sin una interpretación correcta. El análisis numérico es el primer paso de una serie de etapas iterativas en la búsqueda de lo que los datos nos quieren decir, si somos lo suficientemente pacientes para escucharlos.

Este capitulo abarcará, con unas pocas funciones, el análisis numérico completo de datos. Esto debería ser el primer paso en cualquier proyecto de datos, donde comenzamos sabiendo cuáles son los tipos correctos de datos y exploramos las distribuciones de variables numéricas y categóricas.

También se enfocará en la extracción de conclusiones semánticas, que será útil a la hora de escribir informes para audiencias no especializadas.

¿Qué vamos a repasar en este capítulo?

Estado de salud de un conjunto de datos:
- Obtener métricas como el número total de filas, columnas, tipos de datos, ceros, y valores faltantes
- Cómo cada uno de los ítems mencionados impactan sobre diferentes análisis
- Cómo filtrar y operar rápidamente sobre (y con) ellos para limpiar los datos
Análisis univariado en una variable categórica:
- Frecuencia, porcentaje, valor acumulativo, y gráficos coloridos
Análisis univariado con variables numéricas:
- Percentil, dispersión, desvío estándar, promedio, valores máximos y mínimos
- Percentil vs. cuantil vs. cuartil
- Curtosis, asimetría, rango intercuartil, coeficiente de variación
- Gráficos de distribuciones
- Estudio de caso completo basado en “Data World”, preparación de datos, y análisis de datos

Repaso de funciones utilizadas en el capítulo:

df_status(data): Análisis de la estructura del conjunto de datos
describe(data): Análisis numérico y categórico (cuantitativo)
freq(data): Análisis categórico (cuantitativo y gráfico)
profiling_num(data): Análisis para variables numéricas (cuantitativas)
plot_num(data): Análisis para variables numéricas (gráficos)

Note: describe se encuentra en el paquete Hmisc mientras que el resto de las funciones se encuentran en funModeling.

1.1.1 Estado de salud de un conjunto de datos

La cantidad de ceros, NA, Inf, valores únicos al igual que el tipo de datos puede llevar a un buen o mal modelo. Aquí, un acercamiento al primer paso del modelado de datos.

Primero, vamos a cargar las bibliotecas funModeling y dplyr.

# ¡Cargar funModeling!
library(funModeling)
library(dplyr)
data(heart_disease)

1.1.1.1 Buscar valores faltantes, ceros, tipos de datos y valores únicos

Probablemente uno de los primeros pasos, cuando recibimos un nuevo conjunto de datos para analizar, es verificar si existen valores faltantes (NA en R) y el tipo de datos.

La función df_status incluida en funModeling nos puede ayudar mostrándonos estas cifras en valores relativos y porcentuales. También obtiene las estadísticas de infinitos y ceros.

# Analizar los datos ingresados
df_status(heart_disease)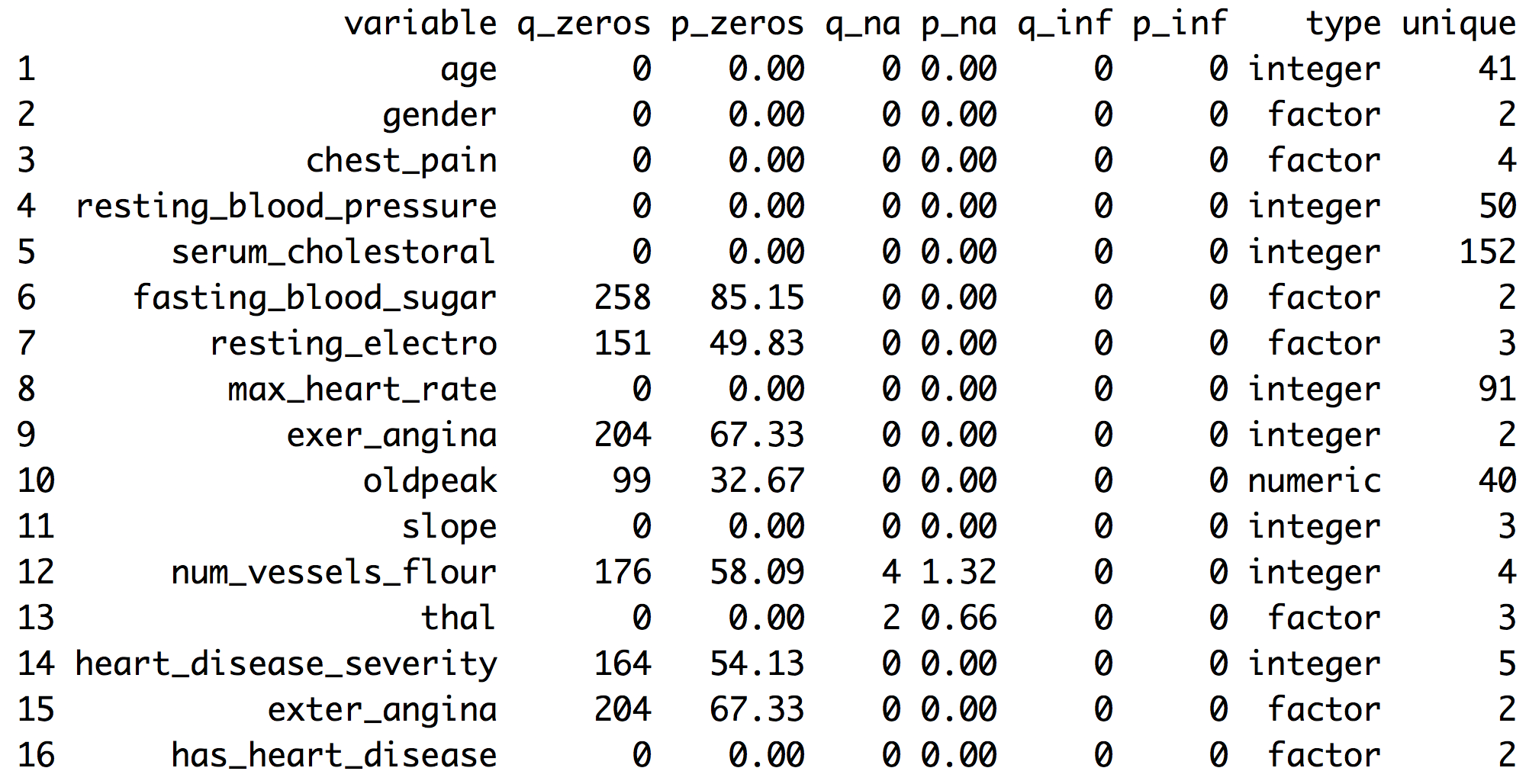

Figure 1.1: Estado de salud de un conjunto de datos

q_zeros: cantidad de ceros (p_zeros: en porcentaje)
q_inf: cantidad de valores infinitos (p_inf: en porcentaje)
q_na: cantidad de NA (p_na: en porcentaje)
type: factor o numérico
unique: cantidad de valores únicos

1.1.1.2 ¿Por qué son importantes estas métricas?

Ceros: Las variables con muchos ceros pueden no ser útiles para modelar y, en algunos casos, pueden sesgar dramáticamente el modelo.
NA: Varios modelos excluyen automáticamente las filas que tienen valores NA (random forest por ejemplo). En consecuencia, el modelo final puede resultar sesgado debido a varias filas faltantes por una sola variable. Por ejemplo, si los datos contienen tan sólo una de las 100 variables con el 90% de datos NA, el modelo se ejecutará con sólo el 10% de las filas originales.
Inf: Los valores infinitos pueden ocasionar un comportamiento inesperado en algunas funciones en R.
Type: Algunas variables están codificadas como números, pero son códigos o categorías y los modelos no las manejan de la misma manera.
Unique: Las variables factor/categóricas con un alto número de valores diferentes (~30) tienden a sobreajustar si las categorías tienen una baja cardinalidad (árboles de decisión, por ejemplo).

1.1.1.3 Filtrar casos no deseados

La función df_status toma un data frame y genera una tabla de estado que nos puede ayudar a quitar rápidamente atributos (o variables) en base a todas las métricas descriptas en la sección anterior. Por ejemplo:

Quitar variables con un alto número de ceros

# Analizar los datos ingresados
my_data_status=df_status(heart_disease, print_results = F)

# Quitar las variables que tienen un 60% de valores cero
vars_to_remove=filter(my_data_status, p_zeros > 60)  %>% .$variable
vars_to_remove

## [1] "fasting_blood_sugar" "exer_angina"         "exter_angina"

# Conservar todas las columnas excepto aquellas presentes en el vector 'vars_to_remove'
heart_disease_2=select(heart_disease, -one_of(vars_to_remove))

Ordenar datos según el porcentaje de ceros

arrange(my_data_status, -p_zeros) %>% select(variable, q_zeros, p_zeros)

##                  variable q_zeros p_zeros
## 1     fasting_blood_sugar     258   85.15
## 2             exer_angina     204   67.33
## 3            exter_angina     204   67.33
## 4       num_vessels_flour     176   58.09
## 5  heart_disease_severity     164   54.13
## 6         resting_electro     151   49.83
## 7                 oldpeak      99   32.67
## 8                     age       0    0.00
## 9                  gender       0    0.00
## 10             chest_pain       0    0.00
## 11 resting_blood_pressure       0    0.00
## 12      serum_cholestoral       0    0.00
## 13         max_heart_rate       0    0.00
## 14                  slope       0    0.00
## 15                   thal       0    0.00
## 16      has_heart_disease       0    0.00

El mismo razonamiento aplica cuando queremos quitar (o conservar) aquellas variables que estén por encima o por debajo de determinado umbral. Por favor revisen el capítulo de valores faltantes para obtener más informaación sobre las implicancias de trabajar con variables que contienen valores faltantes.

1.1.1.4 Profundizar en estos temas

Los valores que devuelve la función df_status son abordados en profundidad en otros capítulos:

Valores faltantes el tratamiento, análisis e imputación de (NA) son abordados en el capítulo Datos faltantes.
Tipos de datos, las conversiones e implicancias de trabajar con distintos tipos de datos y más temas son abordados en el capítulo Tipos de datos.
Un alto número de valores únicos es sinónimo de variables de alta cardinalidad. Estudiamos esta situación en los siguientes capítulos:
- Variables de alta cardinalidad en estadística descriptiva
- Variables de alta cardinalidad en modelado predictivo

1.1.1.5 Obtener otras estadísticas comunes: cantidad total de filas, cantidad total de columnas y nombres de columnas:

# Cantidad total de filas
nrow(heart_disease)

## [1] 303

# Cantidad total de columnas
ncol(heart_disease)

## [1] 16

# Nombres de columnas
colnames(heart_disease)

##  [1] "age"                    "gender"                
##  [3] "chest_pain"             "resting_blood_pressure"
##  [5] "serum_cholestoral"      "fasting_blood_sugar"   
##  [7] "resting_electro"        "max_heart_rate"        
##  [9] "exer_angina"            "oldpeak"               
## [11] "slope"                  "num_vessels_flour"     
## [13] "thal"                   "heart_disease_severity"
## [15] "exter_angina"           "has_heart_disease"

1.1.2 Análisis de variables categóricas

Asegúrense de tener la última version de ‘funModeling’ (>= 1.6).

La función freq simplifica el análisis de frecuencia o distribución. Dicha función vuelca la distribución en una tabla y en un gráfico (por defecto) y muestra la distribución de números absolutos y relativos.

Si desean obtener la distribución de dos variables:

freq(data=heart_disease, input = c('thal','chest_pain'))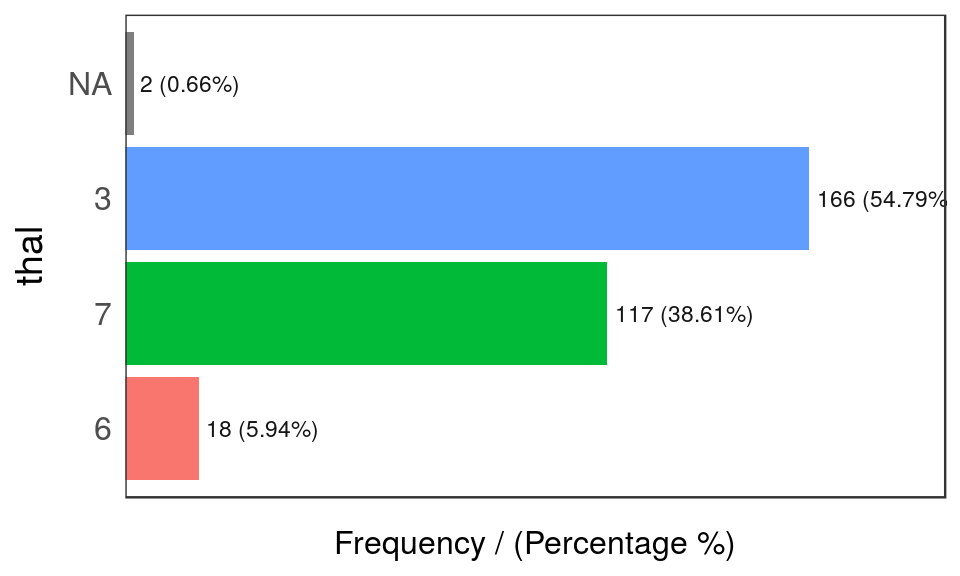

Figure 1.2: Análisis de frecuencia 1

##   thal frequency percentage cumulative_perc
## 1    3       166      54.79           54.79
## 2    7       117      38.61           93.40
## 3    6        18       5.94           99.34
## 4 <NA>         2       0.66          100.00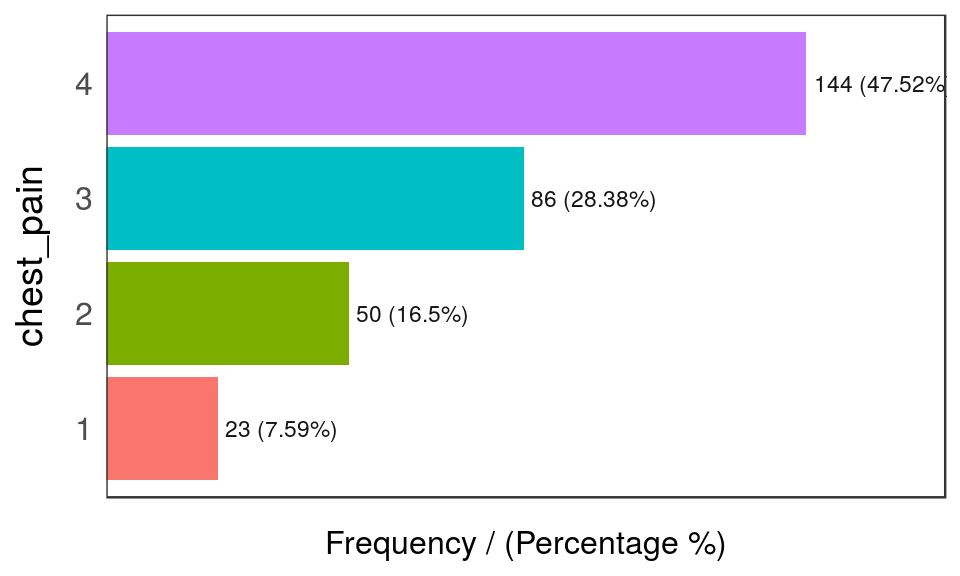

Figure 1.2: Análisis de frecuencia 2

##   chest_pain frequency percentage cumulative_perc
## 1          4       144      47.52           47.52
## 2          3        86      28.38           75.90
## 3          2        50      16.50           92.40
## 4          1        23       7.59          100.00

## [1] "Variables processed: thal, chest_pain"

Al igual que en las demás funciones de funModeling, si falta input, entonces la función se ejecutará para todas las variables factor o de carácter que estén presentes en un data frame dado:

freq(data=heart_disease)

Si sólo queremos obtener la tabla sin el gráfico, entonces configuramos el parámetro plot como FALSE. El ejemplo freq también puede trabajar con una variable singular. Por defecto, los valores NA son considerados tanto en la tabla como en el gráfico. Si es necesario excluir los valores NA, entonces ingresen na.rm = TRUE. Verán ambos ejemplos a continuación:

freq(data=heart_disease$thal, plot = FALSE, na.rm = TRUE)

Si sólo se brinda una variable, entonces freq generará la tabla; por lo tanto, es fácil realizar algunos cálculos en base a las variables que brinda.

Por ejemplo, para visualizar las categorías que representan la mayor parte del 80% (en base a cumulative_perc < 80).
Para obtener las categorías que pertenecen a la cola larga, es decir, filtrando por percentage < 1 e identificando aquellas categorías que aparecen menos del 1% de las veces.

Además, al igual que con las demás funciones para graficar que están incluidas en el paquete, si es necesario exportar gráficos, agreguen el parámetro path_out, que creará la carpeta si aún no ha sido creada.

freq(data=heart_disease, path_out='my_folder')

1.1.2.0.1 Análisis

Los resultados están ordenados según la variable frequency, que rápidamente analiza las categorías con mayor frecuencia y qué porcentaje representan (variable cummulative_perc). En términos generales, a los seres humanos nos gusta el orden. Si las variables no están ordenadas, nuestros ojos empiezan a moverse por todas las barras para compararlas y nuestros cerebros ubican cada barra en relación a las demás.

Comprueben la diferencia entre los mismos datos ingresados, primero sin ordenar y luego ordenados:

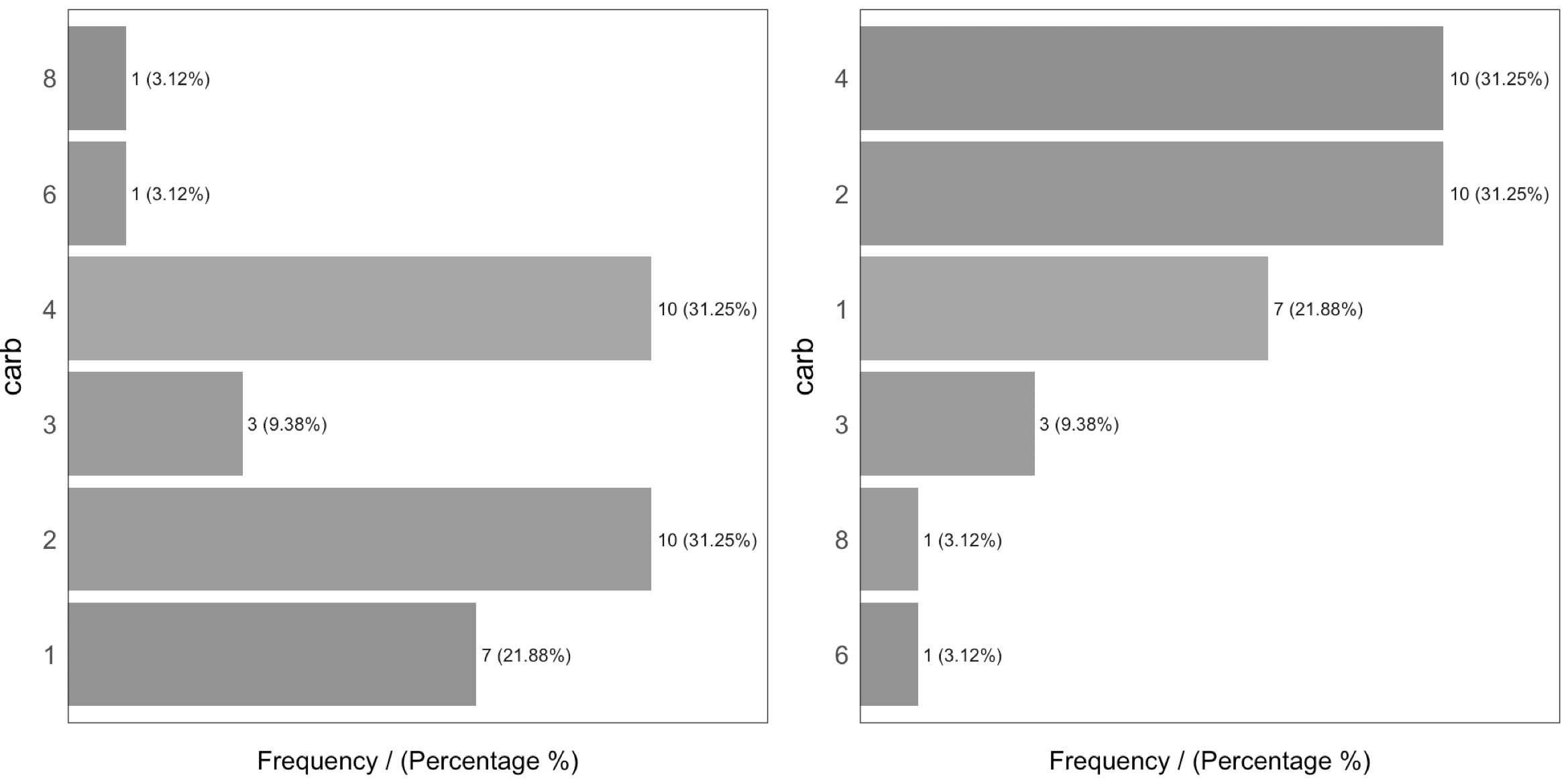
Figure 1.3: Orden y belleza

En general, suele haber unas pocas categorías que aparecen la mayor parte del tiempo.

Pueden encontrar un análisis más completo en Variables de alta cardinalidad en estadística descriptiva

1.1.2.1 Introduciendo la función `describe`

Esta función está incluida en el paquete Hmisc y nos permite analizar rápidamente un conjunto de datos completo para variables númericas y categóricas. En este caso, seleccionaremos sólo dos variables y analizaremos el resultado.

# Conservar solamente las dos variables que utilizaremos en este ejemplo
heart_disease_3=select(heart_disease, thal, chest_pain)

# ¡Analizar los datos!
describe(heart_disease_3)

## heart_disease_3 
## 
##  2  Variables      303  Observations
## ---------------------------------------------------------------------------
## thal 
##        n  missing distinct 
##      301        2        3 
##                             
## Value          3     6     7
## Frequency    166    18   117
## Proportion 0.551 0.060 0.389
## ---------------------------------------------------------------------------
## chest_pain 
##        n  missing distinct 
##      303        0        4 
##                                   
## Value          1     2     3     4
## Frequency     23    50    86   144
## Proportion 0.076 0.165 0.284 0.475
## ---------------------------------------------------------------------------

Donde:

n: cantidad de filas que no son NA. En este caso, indica que hay 301 pacientes que contienen un número.
missing: cantidad de valores faltantes. Al sumar este indicador y n, obtenemos la cantidad total de filas.
unique: cantidad de valores únicos (o distintos).

El resto de la información es bastante similar a la función freq e indica entre paréntesis el número total en valores relativos y absolutos para cada categoría diferente.

1.1.3 Análisis de variables numéricas

Esta sección se divide en dos partes:

Parte 1: Introducción al caso de estudio “World Data”
Parte 2: Hacer el análisis numérico en R

Si no desean saber cómo se calcula la etapa de preparación de datos de Data World, pueden saltar a “Parte 2: Haciendo el análisis numérico en R”, cuando el análisis comenzó.

1.1.3.1 Parte 1: Introducción al caso de estudio “World Data”

Este estudio contiene muchos indicadores sobre el desarrollo mundial. Independientemente del ejemplo de análisis numérico, la idea es proveer una tabla lista para usar para sociólogos, investigadores, etc. interesados en analizar este tipo de datos.

La fuente original de los datos es: http://databank.worldbank.org. Allí encontrarán un diccionario de datos que explica todas las variables.

Primero, tenemos que hacer una limpieza de datos. Vamos a conservar el valor más reciente de cada indicador.

library(Hmisc)

# Cargar datos desde el repositorio de libros sin alterar el formato
data_world=read.csv(file = "https://goo.gl/2TrDgN", header = T, stringsAsFactors = F, na.strings = "..")

# Excluir los valores faltantes en Series.Code. Los datos descargados de la página web contienen cuatro líneas con "free-text" en la parte inferior del archivo.
data_world=filter(data_world, Series.Code!="")

# La función mágica que conserva los valores más recientes de cada métrica. Si no están familiarizados con R, entonces salten esta parte.
max_ix<-function(d) 
{
  ix=which(!is.na(d))
  res=ifelse(length(ix)==0, NA, d[max(ix)])
  return(res)
}

data_world$newest_value=apply(data_world[,5:ncol(data_world)], 1, FUN=max_ix)

# Visualizar las primeras tres filas
head(data_world, 3)

##                                          Series.Name       Series.Code
## 1 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS
## 2 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS
## 3 Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS
##   Country.Name Country.Code X1990..YR1990. X2000..YR2000. X2007..YR2007.
## 1  Afghanistan          AFG             NA             NA             NA
## 2      Albania          ALB             NA             NA             NA
## 3      Algeria          DZA           11.8             NA             NA
##   X2008..YR2008. X2009..YR2009. X2010..YR2010. X2011..YR2011.
## 1             NA             NA             NA             NA
## 2             NA             NA             NA             NA
## 3             NA             NA             NA             NA
##   X2012..YR2012. X2013..YR2013. X2014..YR2014. X2015..YR2015.
## 1             NA             NA           62.7             NA
## 2             NA             NA             NA             NA
## 3             NA             NA             NA             NA
##   X2016..YR2016. newest_value
## 1             NA         62.7
## 2             NA           NA
## 3             NA         11.8

Las columnas Series.Name y Series.Code son los indicadores a analizar. Country.Name y Country.Code son los países. Cada fila representa una combinación única de país e indicador. Las columnas restantes, X1990..YR1990. (año 1990),X2000..YR2000. (año 2000), X2007..YR2007. (año 2007), y sucesivamente indican el valor de cada métrica para ese año, cada columna corresponde a un año.

1.1.3.2 Tomar decisiones como científicos de datos

Hay muchas celdas NAs porque algunos países no cuentan con las mediciones de los indicadores en esos años. En este punto, debemos tomar una decisión como científicos de datos. Probablemente no tomemos la decisión óptima si no consultamos con un experto, por ejemplo, un sociólogo.

¿Qué hacemos con los valores NA? En este caso, vamos a conservar el valor más reciente para todos los indicadores. Quizás esta no sea la mejor manera de extraer conclusiones para un paper académico, ya que vamos a comparar algunos países que cuentan con información actualizada al 2016 con países cuyos datos fueron actualizados por última vez en el 2009. Comparar todos los indicadores con los datos más recientes es un enfoque apropiado para un primer análisis.

Otra solución podría haber sido conservar el valor más reciente solamente si este es de los últimos cinco años. Esto reduciría la cantidad de países a analizar.

Estas preguntas son imposibles de responder para un sistema de inteligencia artificial, no obstante la decisión puede influir drásticamente en los resultados.

La última transformación

El próximo paso convertirá la última tabla de formato largo a ancho. En otras palabras, cada fila representará un país y cada columna un indicador (gracias a la última transformación que tiene el valor más reciente para cada combinación de indicador-país).

Los nombres de los indicadores son poco claros, por lo que “traduciremos” algunos de ellos.

# Obtener la lista de descripciones de indicadores.
names=unique(select(data_world, Series.Name, Series.Code))
head(names, 5)

##                                            Series.Name       Series.Code
## 1   Population living in slums (% of urban population) EN.POP.SLUM.UR.ZS
## 218                    Income share held by second 20%    SI.DST.02ND.20
## 435                     Income share held by third 20%    SI.DST.03RD.20
## 652                    Income share held by fourth 20%    SI.DST.04TH.20
## 869                   Income share held by highest 20%    SI.DST.05TH.20

# Convertir algunos
df_conv_world=data.frame(
  new_name=c("urban_poverty_headcount", 
             "rural_poverty_headcount", 
             "gini_index", 
             "pop_living_slums",
             "poverty_headcount_1.9"), 
  Series.Code=c("SI.POV.URHC", 
                "SI.POV.RUHC",
                "SI.POV.GINI",
                "EN.POP.SLUM.UR.ZS",
                "SI.POV.DDAY"), 
  stringsAsFactors = F)

# Agregar el nuevo valor del indicador
data_world_2 = left_join(data_world, 
                         df_conv_world, 
                         by="Series.Code", 
                         all.x=T)

data_world_2 = 
  mutate(data_world_2, Series.Code_2=
           ifelse(!is.na(new_name), 
                  as.character(data_world_2$new_name), 
                  data_world_2$Series.Code)
         )

El significado de cualquiera de los indicadores puede cotejarse en data.worldbank.org. Por ejemplo, si queremos saber qué significa EN.POP.SLUM.UR.ZS, ingresamos a: http://data.worldbank.org/indicator/EN.POP.SLUM.UR.ZS

# El paquete 'reshape2' contiene tanto la función 'dcast' como 'melt'
library(reshape2)

data_world_wide=dcast(data_world_2, Country.Name  ~ Series.Code_2, value.var = "newest_value")

Nota: Para entender más acerca de los formatos largo y ancho utilizando el paquete reshape2, y cómo convertir de uno a otro, por favor diríjanse a: http://seananderson.ca/2013/10/19/reshape.html.

Ahora tenemos la tabla final para analizar:

# Visualizar las primeras tres filas
head(data_world_wide, 3)

##   Country.Name gini_index pop_living_slums poverty_headcount_1.9
## 1  Afghanistan         NA             62.7                    NA
## 2      Albania      28.96               NA                  1.06
## 3      Algeria         NA             11.8                    NA
##   rural_poverty_headcount SI.DST.02ND.20 SI.DST.03RD.20 SI.DST.04TH.20
## 1                    38.3             NA             NA             NA
## 2                    15.3          13.17          17.34          22.81
## 3                     4.8             NA             NA             NA
##   SI.DST.05TH.20 SI.DST.10TH.10 SI.DST.FRST.10 SI.DST.FRST.20 SI.POV.2DAY
## 1             NA             NA             NA             NA          NA
## 2          37.82          22.93           3.66           8.85        6.79
## 3             NA             NA             NA             NA          NA
##   SI.POV.GAP2 SI.POV.GAPS SI.POV.NAGP SI.POV.NAHC SI.POV.RUGP SI.POV.URGP
## 1          NA          NA         8.4        35.8         9.3         5.6
## 2        1.43        0.22         2.9        14.3         3.0         2.9
## 3          NA          NA          NA         5.5         0.8         1.1
##   SI.SPR.PC40 SI.SPR.PC40.ZG SI.SPR.PCAP SI.SPR.PCAP.ZG
## 1          NA             NA          NA             NA
## 2        4.08        -1.2205        7.41        -1.3143
## 3          NA             NA          NA             NA
##   urban_poverty_headcount
## 1                    27.6
## 2                    13.6
## 3                     5.8

1.1.3.3 Parte 2: Hacer el análisis numérico en R

Utilizaremos las siguientes funciones:

describe de Hmisc
profiling_num (análisis univariado completo), y plot_num (histogramas) de funModeling

Seleccionaremos solamente dos variables como ejemplo:

library(Hmisc) # contiene la función `describe`

vars_to_profile=c("gini_index", "poverty_headcount_1.9")
data_subset=select(data_world_wide, one_of(vars_to_profile))

# Utilizar la función `describe` en con junto de datos completo. 
# Puede ejecutarse con una variable; por ejemplo, describe(data_subset$poverty_headcount_1.9)

describe(data_subset)

## data_subset 
## 
##  2  Variables      217  Observations
## ---------------------------------------------------------------------------
## gini_index 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##      140       77      136        1     38.8    9.594    26.81    27.58 
##      .25      .50      .75      .90      .95 
##    32.35    37.69    43.92    50.47    53.53 
## 
## lowest : 24.09 25.59 25.90 26.12 26.13, highest: 56.24 60.46 60.79 60.97 63.38
## ---------------------------------------------------------------------------
## poverty_headcount_1.9 
##        n  missing distinct     Info     Mean      Gmd      .05      .10 
##      116      101      107        1    18.33    23.56    0.025    0.075 
##      .25      .50      .75      .90      .95 
##    1.052    6.000   33.815   54.045   67.328 
## 
## lowest :  0.00  0.01  0.03  0.04  0.06, highest: 68.64 68.74 70.91 77.08 77.84
## ---------------------------------------------------------------------------

Tomando poverty_headcount_1.9 (Índice de pobreza de US$1.90 por día es el porcentaje de la población que vive con menos de US$1.90 por día a precios internacionales de 2011.), lo podemos describir como:

n: cantidad de filas que no son NA. En este caso, indica que hay 116 países que contienen un número.
missing: cantidad de valores faltantes. Al sumar este indicador y n, obtenemos la cantidad total de filas. Casi la mitad de los países no tienen datos.
unique: cantidad de valores únicos (o distintos).
Info: un estimador de la cantidad de información presente en la variable y que no es importante en este punto.
Mean: el clásico promedio o media.
Números: .05, .10, .25, .50, .75, .90 y .95 son percentiles. Estos valores son muy útiles ya que nos ayudan a describir la distribución. Cubriremos este tema en profundidad más adelante, pero, por ejemplo, .05 es el 5to percentil.
lowest y highest: los cinco valores mínimos/máximos. Aquí podemos detectar valores atípicos y errores de datos. Por ejemplo, si la variable representa un porcentaje, entonces no puede contener valores negativos.

La siguiente función es profiling_num, que toma un data frame y devuelve una gran tabla en la que es fácil sentirse abrumado por un mar de métricas. Es similar a lo que vemos en la película Matrix.

Figure 1.4: La matrix de datos

Imagen de la película “Matrix” (1999), dirigida por las hermanas Wachowski.

La idea de la siguiente tabla es brindarle al usuario un conjunto completo de métricas para que él o ella pueda decidir cuáles utilizar para el estudio.

Nota: Detrás de cada métrica hay mucha teoría estadística. Aquí cubriremos solamente un enfoque acotado y muy simplificado para introducir los conceptos.

library(funModeling)

# El análisis numérico completo de una función automáticamente excluye las variables no numéricas
profiling_num(data_world_wide)

##                   variable mean std_dev variation_coef   p_01   p_05
## 1               gini_index 38.8    8.49           0.22 25.711 26.815
## 2         pop_living_slums 45.7   23.66           0.52  6.830 10.750
## 3    poverty_headcount_1.9 18.3   22.74           1.24  0.000  0.025
## 4  rural_poverty_headcount 41.2   21.91           0.53  2.902  6.465
## 5           SI.DST.02ND.20 10.9    2.17           0.20  5.568  7.361
## 6           SI.DST.03RD.20 15.2    2.03           0.13  9.137 11.828
## 7           SI.DST.04TH.20 21.5    1.49           0.07 16.286 18.288
## 8           SI.DST.05TH.20 45.9    7.14           0.16 35.004 36.360
## 9           SI.DST.10TH.10 30.5    6.75           0.22 20.729 21.988
## 10          SI.DST.FRST.10  2.5    0.87           0.34  0.916  1.147
## 11          SI.DST.FRST.20  6.5    1.87           0.29  2.614  3.369
## 12             SI.POV.2DAY 32.4   30.64           0.95  0.061  0.393
## 13             SI.POV.GAP2 14.2   16.40           1.16  0.012  0.085
## 14             SI.POV.GAPS  6.9   10.10           1.46  0.000  0.000
## 15             SI.POV.NAGP 12.2   10.12           0.83  0.421  1.225
## 16             SI.POV.NAHC 30.7   17.88           0.58  1.842  6.430
## 17             SI.POV.RUGP 15.9   11.83           0.75  0.740  1.650
## 18             SI.POV.URGP  8.3    8.24           0.99  0.300  0.900
## 19             SI.SPR.PC40 10.3    9.75           0.95  0.857  1.228
## 20          SI.SPR.PC40.ZG  2.0    3.62           1.85 -6.232 -3.021
## 21             SI.SPR.PCAP 21.1   17.44           0.83  2.426  3.138
## 22          SI.SPR.PCAP.ZG  1.5    3.21           2.20 -5.897 -3.805
## 23 urban_poverty_headcount 23.3   15.06           0.65  0.579  3.140
##      p_25 p_50 p_75 p_95 p_99 skewness kurtosis  iqr       range_98
## 1  32.348 37.7 43.9 53.5 60.9    0.552      2.9 11.6  [25.71, 60.9]
## 2  25.175 46.2 65.6 83.4 93.4    0.087      2.0 40.5  [6.83, 93.41]
## 3   1.052  6.0 33.8 67.3 76.2    1.125      2.9 32.8     [0, 76.15]
## 4  25.250 38.1 57.6 75.8 81.7    0.051      2.0 32.3    [2.9, 81.7]
## 5   9.527 11.1 12.6 14.2 14.6   -0.411      2.7  3.1  [5.57, 14.57]
## 6  13.877 15.5 16.7 17.9 18.1   -0.876      3.8  2.8  [9.14, 18.14]
## 7  20.758 21.9 22.5 23.0 23.4   -1.537      5.6  1.8 [16.29, 23.39]
## 8  40.495 44.8 49.8 58.1 65.9    0.738      3.3  9.3    [35, 65.89]
## 9  25.710 29.5 34.1 42.2 50.6    0.905      3.6  8.4 [20.73, 50.62]
## 10  1.885  2.5  3.2  3.9  4.3    0.043      2.2  1.4   [0.92, 4.35]
## 11  5.092  6.5  8.0  9.4 10.0   -0.119      2.2  2.9     [2.61, 10]
## 12  3.828 20.3 63.2 84.6 90.3    0.536      1.8 59.4  [0.06, 90.34]
## 13  1.305  5.5 26.3 48.5 56.2    1.063      2.9 25.0  [0.01, 56.18]
## 14  0.287  1.4 10.3 31.5 38.3    1.654      4.7 10.0     [0, 38.29]
## 15  4.500  8.7 16.9 32.4 36.7    1.129      4.0 12.4  [0.42, 36.72]
## 16 16.350 26.6 44.2 63.0 71.6    0.529      2.4 27.9  [1.84, 71.64]
## 17  5.950 13.6 22.5 37.7 45.3    0.801      3.0 16.5  [0.74, 45.29]
## 18  2.900  6.3  9.9 25.1 35.2    2.316      9.8  7.0   [0.3, 35.17]
## 19  3.475  6.9 12.7 28.9 35.4    1.251      3.4  9.2  [0.86, 35.35]
## 20 -0.084  1.7  4.6  7.9  9.0   -0.294      3.3  4.7     [-6.23, 9]
## 21  8.003 15.3 25.4 52.8 67.2    1.132      3.3 17.4  [2.43, 67.17]
## 22 -0.486  1.3  3.6  7.0  8.5   -0.018      3.6  4.0   [-5.9, 8.48]
## 23 12.708 20.1 31.2 51.0 61.8    0.730      3.0 18.5  [0.58, 61.75]
##          range_80
## 1  [27.58, 50.47]
## 2    [12.5, 75.2]
## 3   [0.08, 54.05]
## 4  [13.99, 71.99]
## 5    [8.28, 13.8]
## 6   [12.67, 17.5]
## 7  [19.73, 22.81]
## 8  [36.99, 55.24]
## 9  [22.57, 39.89]
## 10   [1.48, 3.67]
## 11   [3.99, 8.89]
## 12  [0.79, 78.29]
## 13  [0.16, 40.85]
## 14  [0.02, 23.45]
## 15     [1.85, 27]
## 16  [9.86, 58.22]
## 17    [3.3, 32.2]
## 18    [1.3, 19.1]
## 19  [1.81, 27.63]
## 20  [-2.64, 6.48]
## 21  [4.25, 49.22]
## 22  [-2.07, 5.17]
## 23  [5.98, 46.11]

Cada indicador tiene su raison d’être:

variable: nombre de la variable
mean: el famoso promedio o media
std_dev: desvío estándar, una medida de dispersión o extensión con respecto al valor promedio. Un valor cerca de 0 indica que casi no hay variación (por lo que parece más una constante); por otro lado, es más difícil definir qué sería un valor alto, pero podemos decir que a mayor variación, mayor dispersión. El caos se asemeja a un desvío estándar de valor infinito. La unidad es la misma que la del promedio para que puedan compararse.
variation_coef: coeficiente de variación=std_dev/mean. Dado que el std_dev es un valor absoluto, es bueno tener un indicador que lo exprese en un valor relativo, comparando el std_dev contra el mean Un valor de 0.22 indica que el std_dev es el 22% del mean. Si estuviera cerca de 0 entonces la variable estaría más centrada cerca del promedio. Si comparamos dos clasificadores, entonces es probable que prefiramos el que tenga menores std_dev y variation_coef por su precisión.
p_01, p_05, p_25, p_50, p_75, p_95, p_99: Percentiles en 1%, 5%, 25%, y así sucesivamente. Encontrarán un repaso completo sobre percentiles más adelante en este capítulo.

Para leer una explicación completa sobre percentiles, por favor diríjanse a: Anexo 1: La magia de los percentiles.

skewness: es una medida de asimetría. Un valor cercano a 0 indica que la distribución de los datos es igual hacia ambos lados (o simétrica) con respecto al promedio. Un valor positivo implica una larga cola hacia la derecha, mientras que un valor negativo significa lo opuesto.

Después de esta sección, revisen la asimetría en los gráficos. La variable pop_living_slums está cerca de 0 (“igualmente” distribuida), poverty_headcount_1.9 es positiva (cola hacia la derecha), y SI.DST.04TH.20 es negativa (cola hacia la izquierda). Cuanto más lejos esté la asimetría de 0, más probable es que la distribución tenga valores atípicos.

kurtosis: describe las colas de la distribución; dicho en términos simples, un número alto puede indicar la presencia de valores atípicos (tal como veremos más adelante para la variable SI.POV.URGP que tiene un valor atípico cerca de 50). Para leer un repaso completo de asimetría y curtosis, diríjanse a las Referencias (McNeese 2016) y (Handbook 2013).
iqr: el rango intercuartil es el resultado de observar los percentiles 0.25 y 0.75, e indica, en la misma unidad de la variable, el largo de dispersión del 50% de los valores. Cuanto mayor sea el valor, más dispersa es la variable.
range_98 y range_80: indican el rango en el que el se encuentra el 98% de los valores. Quita el 1% inferior y superior (ergo, el número 98%). Es bueno saber cuál es el rango de la variable sin valores atípicos potenciales. Por ejemplo, pop_living_slums va de 0 a 76.15. Es más robusto que comparar los valores mínimos y máximos. range_80 es igual que range_98 pero sin el 10% inferior y superior.

iqr, range_98 y range_80 están basados en percentiles, que cubriremos más adelante en este capítulo.

Importante: Todas las métricas se calculan quitando los valores NA. De lo contrario, la tabla estaría llena de NAs.

1.1.3.3.1 Consejos para utilizar `profiling_num`

La idea de la función profiling_num es proveer al científico de datos un conjunto completo de métricas para que pueda seleccionar las más relevantes. Esto se puede hacer fácilmente utilizando la función select del paquete dplyr.

Además, debemos configurar en profiling_num el parámetro print_results = FALSE. De esta forma, evitamos visualizar en la consola.

Por ejemplo, probemos con mean, p_01, p_99 y range_80:

my_profiling_table=profiling_num(data_world_wide, print_results = FALSE) %>% select(variable, mean, p_01, p_99, range_80)

# Visualizar sólo las primeras tres filas
head(my_profiling_table, 3)

##                variable mean p_01 p_99       range_80
## 1            gini_index   39 25.7   61 [27.58, 50.47]
## 2      pop_living_slums   46  6.8   93   [12.5, 75.2]
## 3 poverty_headcount_1.9   18  0.0   76  [0.08, 54.05]

Noten que profiling_num devuelve una tabla, por lo que podemos filtrar rápidamente los casos de acuerdo a las condiciones que definamos.

1.1.3.3.2 Analizar variables numéricas utilizando gráficos

Otra función de funModeling es plot_num, que toma un conjunto de datos y grafica la distribución de cada variable numérica excluyendo automáticamente las variables no numéricas:

plot_num(data_world_wide)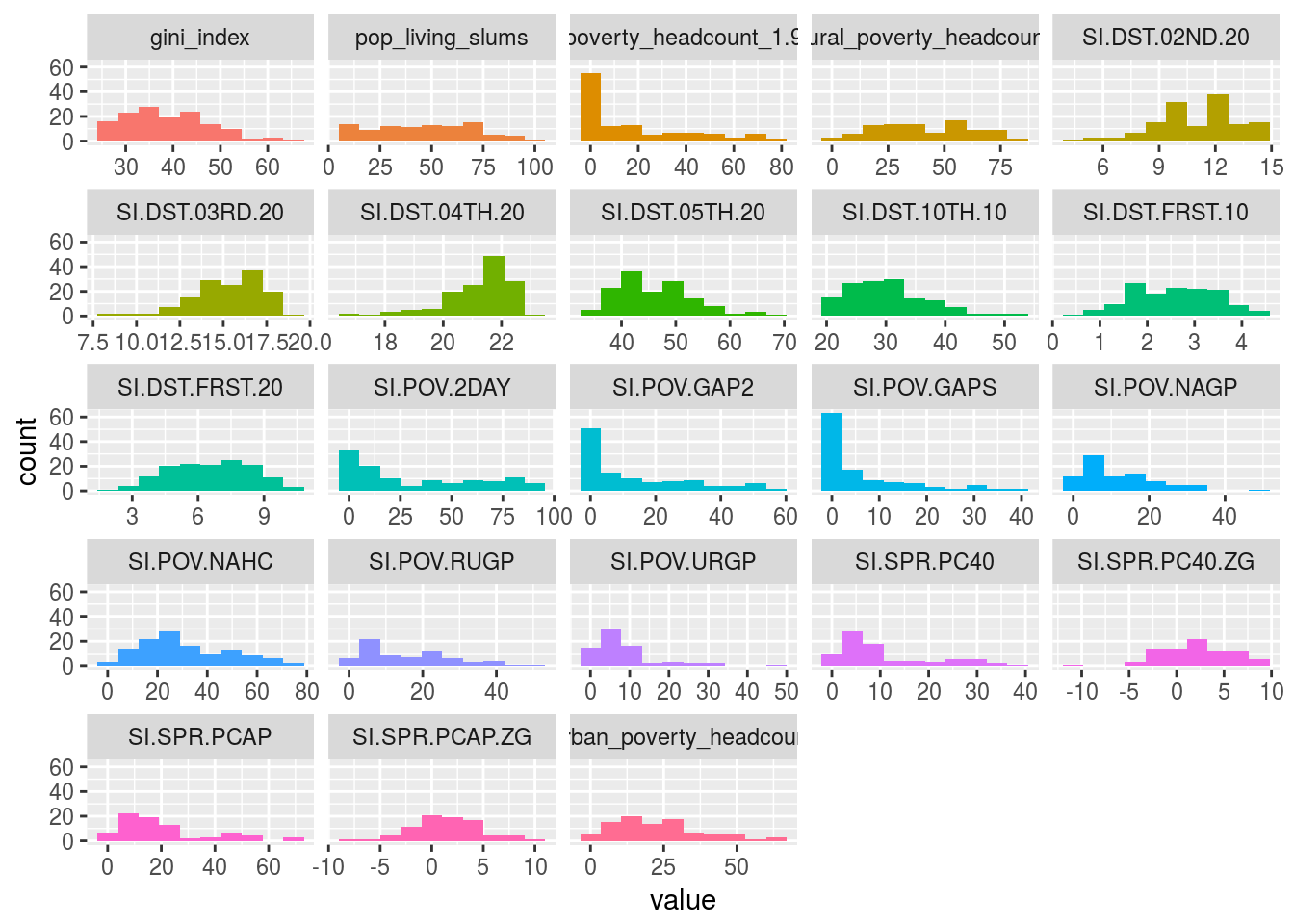

Figure 1.5: Analizando datos numéricos

Podemos ajustar la cantidad de barras del gráfico cambiando el parámetro bins (por defecto está configurado en 10). Por ejemplo: plot_num(data_world_wide, bins = 20).

1.1.4 Reflexiones finales

Hasta aquí, han aparecido muchos números, y aún más en el apéndice de percentiles. Lo importante es que encuentren el enfoque adecuado para explorar sus datos. Puede estar relacionado con las métricas o con otros criterios.

Las funciones df_status, describe, freq, profiling_num y plot_num pueden ejecutarse al principio de un proyecto de datos.

Con respecto al comportamiento normal y anormal de los datos, es importante estudiar ambos. Para describir un conjunto de datos en términos generales, deberíamos excluir los valores extremos: por ejemplo, con la variable range_98. El promedio debería disminuir después de la exclusión.

Estos análisis son univariados; es decir, no tienen en cuenta otras variables (análisis multivariado). Esto estará incluido en este libro más adelante. Mientras tanto, para encontrar la correlación entre variables ingresadas (y de resultados), pueden dirigirse al capítulo de Correlación.

1.2 Correlación y relación

Fractal de Mandelbrot, donde el caos expresa su belleza; fuente de la imagen: Wikipedia.

1.2.1 ¿De qué se trata esto?

Este capítulo contiene aspectos metodológicos y prácticos de la medición de correlación en variables. Veremos que la palabra correlación puede traducirse en “relación funcional”.

En metodología encontrarán el Cuarteto de Anscombe, un conjunto de cuatro gráficos con distribuciones espaciales diferentes, pero que comparten la misma medida de correlación. Iremos un paso más allá recalculando su relación a través de una métrica más robusta (Coeficiente de Información Máxima o MIC, por sus siglas en inglés).

Mencionaremos Teoría de la Información varias veces; aunque por ahora la cubriremos a nivel matemático, está previsto hacerlo. Muchos algoritmos se basan en ella, incluso el aprendizaje profundo (deep learning).

Entender estos conceptos en dimensiones bajas (dos variables) y datos pequeños (un grupo de filas) nos permite entender mejor los datos de alta dimensión. No obstante, algunos casos reales son sólo datos pequeños.

Desde el punto de vista práctico, podrán replicar el análisis con sus propios datos, analizando numéricamente y exponiendo sus relaciones en gráficos sofisticados.

Empecemos por cargar todas las bibliotecas que necesitaremos.

# Cargar las bibliotecas necesarias
library(funModeling) # contiene datos de heart_disease
library(minerva) # contiene estadístico MIC 
library(ggplot2)
library(dplyr)
library(reshape2) 
library(gridExtra) # nos permite realizar 
# dos gráficos en una fila
options(scipen=999) # desactiva la notación científica

1.2.2 Correlación lineal

Quizás la medida de correlación más estándar para las variables numéricas es la R statistic (o coeficiente de Pearson) que va desde 1 correlación positiva hasta -1 correlación negativa. Un valor alrededor de 0 implica que no hay correlación.

Consideren el ejemplo siguiente, que calcula la medida R basada en una variable de destino (por ejemplo, para realizar la ingeniería de factores). La función correlation_table obtiene la métrica R de todas las variables numéricas omitiendo las categóricas/nominales.

correlation_table(data=heart_disease, target="has_heart_disease")

##                 Variable has_heart_disease
## 1      has_heart_disease              1.00
## 2 heart_disease_severity              0.83
## 3      num_vessels_flour              0.46
## 4                oldpeak              0.42
## 5                  slope              0.34
## 6                    age              0.23
## 7 resting_blood_pressure              0.15
## 8      serum_cholestoral              0.08
## 9         max_heart_rate             -0.42

La variable heart_disease_severity es la variable -numérica- más importante; cuanto mayor sea su valor, mayores serán las probabilidades de padecer una enfermedad cardíaca (correlación positiva). Lo contrario de max_heart_rate, que tiene una correlación negativa.

Al elevar este número al cuadrado obtenemos la estadística R-squared (también conocida como R cuadrado o R2), que va desde 0 no hay correlación hasta 1 alta correlación.

El estadístico R está profundamente influenciado por los valores atípicos y las relaciones no lineales.

1.2.2.1 Correlación en el Cuarteto de Anscombe

Observen el Cuarteto de Anscombe, citando a Wikipedia:

Fueron construidos en 1973 por el estadístico Francis Anscombe para demostrar tanto la importancia de graficar los datos antes de analizarlos como el efecto de los valores atípicos sobre las propiedades estadísticas.

1973 y sigue vigente hoy, es fantástico.

Estas cuatro relaciones son diferentes, pero todas tienen la misma R2: 0.816.

El siguiente ejemplo calcula el R2 y grafica cada par.

# Leer los datos del Cuarteto de Anscombe
anscombe_data = 
  read.delim(file="https://goo.gl/mVLz5L", header = T)

# Calcular la correlación (R cuadrado o R2) para 
#cada par, los valores son el mismo: 0.86.
cor_1 = cor(anscombe_data$x1, anscombe_data$y1)
cor_2 = cor(anscombe_data$x2, anscombe_data$y2)
cor_3 = cor(anscombe_data$x3, anscombe_data$y3)
cor_4 = cor(anscombe_data$x4, anscombe_data$y4)

# Definir la función
plot_anscombe <- function(x, y, value, type)
{
  # 'anscombe_data' es una variable global, esto es
  # una mala práctica de programación ;)
  p=ggplot(anscombe_data, aes_string(x,y))  + 
    geom_smooth(method='lm', fill=NA) + 
    geom_point(aes(colour=factor(1), 
                   fill = factor(1)), 
               shape=21, size = 2
               ) + 
    ylim(2, 13) + 
    xlim(4, 19) + 
    theme_minimal() + 
    theme(legend.position="none") + 
    annotate("text", 
             x = 12, 
             y =4.5, 
             label = 
               sprintf("%s: %s", 
                       type, 
                       round(value,2)
                       )
             )  
  
  return(p)
}

# Graficar en una cuadrícula de 2x2
grid.arrange(plot_anscombe("x1", "y1", cor_1, "R2"), 
             plot_anscombe("x2", "y2", cor_2, "R2"), 
             plot_anscombe("x3", "y3", cor_3, "R2"), 
             plot_anscombe("x4", "y4", cor_4, "R2"), 
             ncol=2, 
             nrow=2)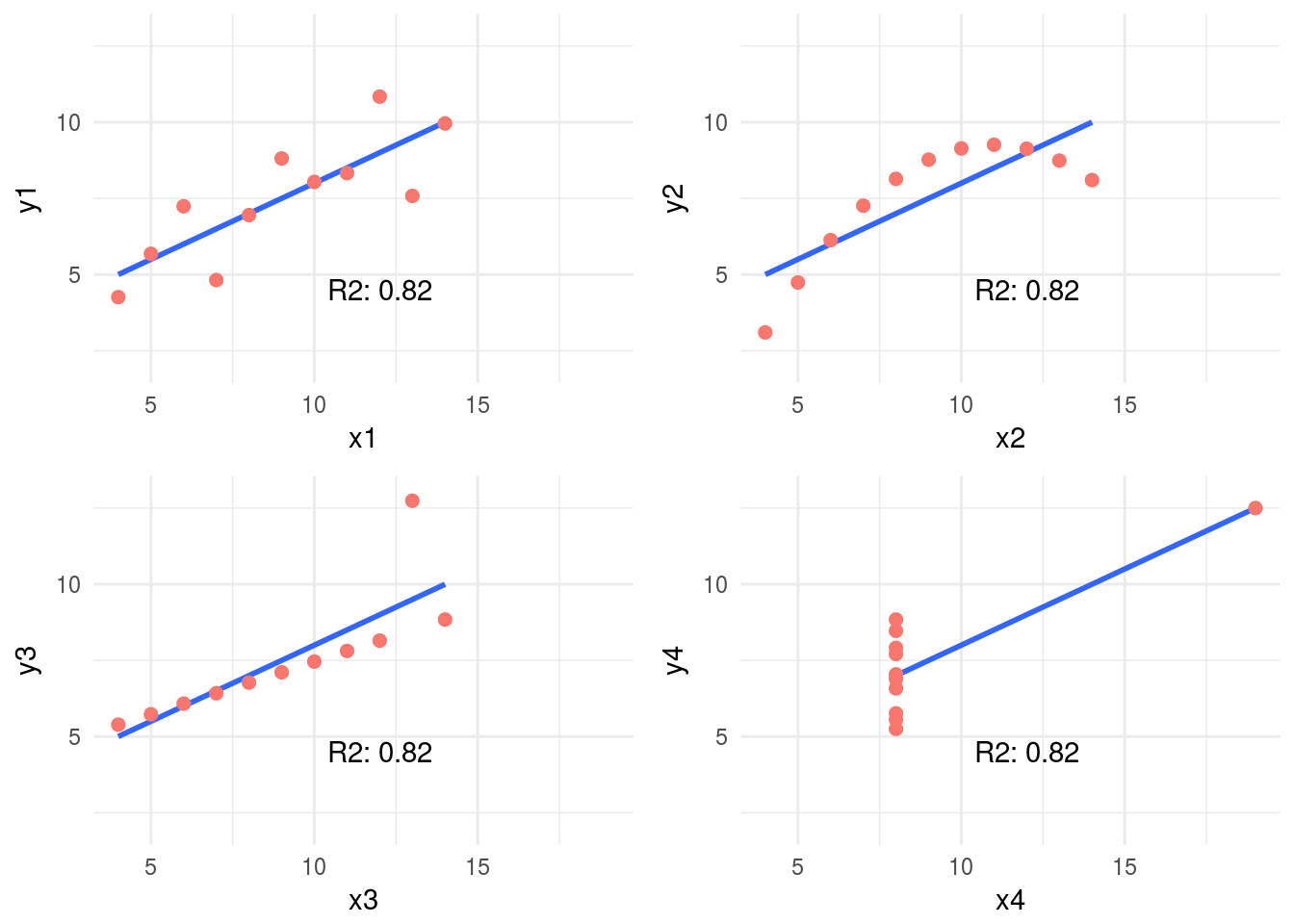

Figure 1.6: Conjunto de Anscombe

4 gráficos diferentes, con el mismo mean para cada variable x y y (9 y 7.501, respectivamente), y el mismo grado de correlación. Pueden comprobar todas las medidas ingresando summary(anscombe_data).

Por esto es tan importante graficar relaciones cuando se analizan las correlaciones.

Volveremos sobre estos datos más tarde. ¡Se pueden mejorar! Primero, introduciremos algunos conceptos de la Teoría de la Información.

1.2.3 Correlación basada en la Teoría de la Información

Estas relaciones pueden medirse mejor con conceptos de la Teoría de la Información. Uno de los muchos algoritmos que se utilizan para medir la correlación basada en esto es MINE, una sigla que significa Maximal Information-based nonparametric exploration, en inglés.

Pueden encontrar la implementación en R en el paquete minerva. También está disponible en otros lenguajes, como Python.

1.2.3.1 Ejemplo en R: Una relación perfecta

Grafiquemos una relación no lineal, basada directamente en una función (exponencial negativa), y visualicemos el valor MIC.

x=seq(0, 20, length.out=500)
df_exp=data.frame(x=x, y=dexp(x, rate=0.65))
ggplot(df_exp, aes(x=x, y=y)) + geom_line(color='steelblue') + theme_minimal()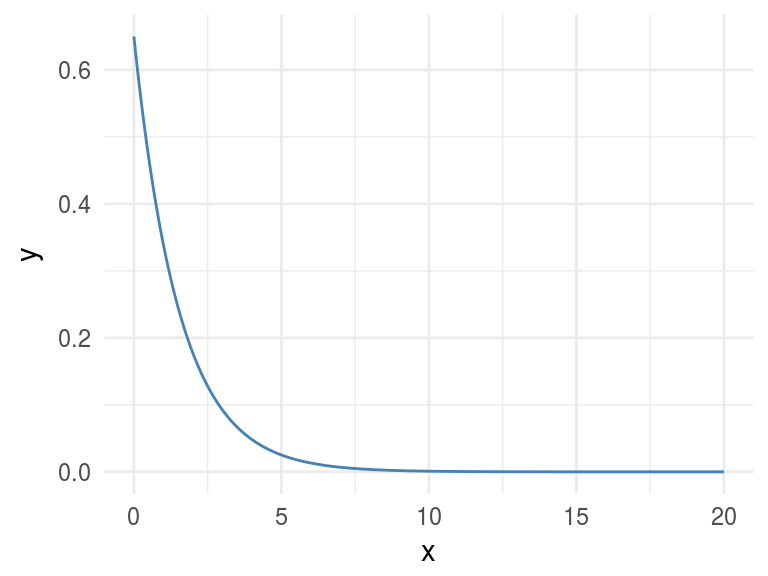

Figure 1.7: Una relación perfecta

# La posición [1,2] contiene la correlación de ambas variables, excluyendo la medida de correlación de cada variable con respecto a sí misma.

# Calcular la correlación lineal
res_cor_R2=cor(df_exp)[1,2]^2
sprintf("R2: %s", round(res_cor_R2,2))

## [1] "R2: 0.39"

# Ahora computamos la métrica MIC
res_mine=mine(df_exp)
sprintf("MIC: %s", res_mine$MIC[1,2])

## [1] "MIC: 1"

Los valores de MIC van de 0 a 1. Cuando es 0, implica que no hay correlación y 1 implica la mayor correlación posible. La interpretación de los valores es la misma que para R cuadrado.

1.2.3.2 Análisis de los resultados

MIC=1 indica que hay una correlación perfecta entre dos variables. Si estamos haciendo ingeniería de factores debemos incluir esta variable.

Más que una simple correlación, lo que dice el MIC es: “Hey, estas dos variables muestran una relación funcional”.

En términos de machine learning (y simplificando demasiado): “la variable y es dependiente de la variable x y una función -no sabemos cuál- puede ser un modelo de la relación entre ellas.”

Esto es delicado porque esa relación fue efectivamente creada a partir de una función, una exponencial.

Pero continuemos con otros ejemplos…

1.2.4 Agregar ruido

El ruido es una señal no deseada que se suma a la original. En machine learning, el ruido contribuye a que el modelo se confunda. En concreto: dos casos idénticos son ingresados -por ejemplo, clientes- y tienen resultados diferentes -uno compra y el otro no.

Ahora vamos a añadir algo de ruido creando la variable y_noise_1.

df_exp$y_noise_1=jitter(df_exp$y, factor = 1000, amount = NULL)
ggplot(df_exp, aes(x=x, y=y_noise_1)) + 
  geom_line(color='steelblue') + theme_minimal()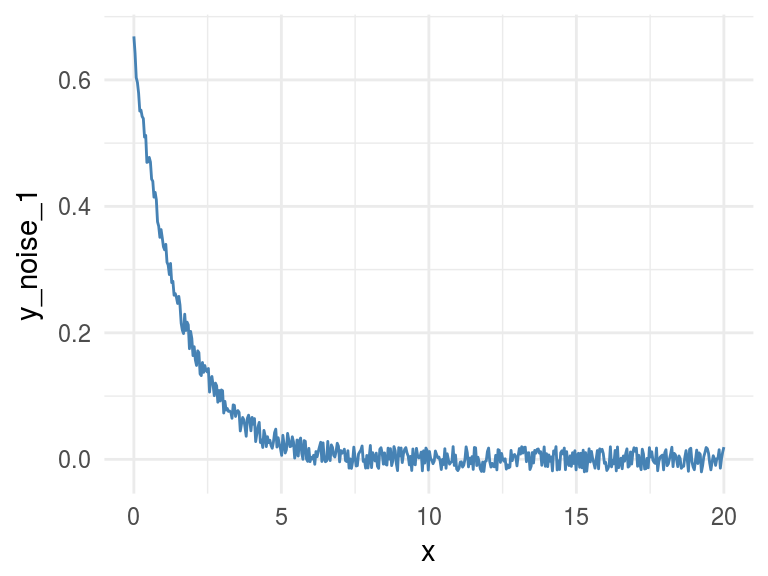

Figure 1.8: Agregando un poco de ruido

Calculando de nuevo la correlación y el MIC, visualizando en ambos casos la matriz completa, que muestra la métrica de correlación/MIC de cada variable de entrada con respecto a todas las demás, incluidas ellas mismas.

# Calcular R cuadrado
res_R2=cor(df_exp)^2
res_R2

##              x    y y_noise_1
## x         1.00 0.39      0.38
## y         0.39 1.00      0.99
## y_noise_1 0.38 0.99      1.00

# Calcular MINE
res_mine_2=mine(df_exp)

# Visualizar MIC 
res_mine_2$MIC

##              x    y y_noise_1
## x         1.00 1.00      0.72
## y         1.00 1.00      0.72
## y_noise_1 0.72 0.72      1.00

Al agregar ruido a los datos, el valor de MIC disminuye de 1 a 0.7226365 (-27%), ¡y eso es genial!

R2 también disminuyó, pero sólo apenas, de 0.3899148 a 0.3866319 (-0.8%).

Conclusión: El MIC refleja una relación ruidosa mucho mejor que R2, y nos ayuda a encontrar asociaciones correlacionadas.

Sobre el último ejemplo: Generar datos basándonos en una función solamente sirve para fines educativos. Pero el concepto de ruido en variables es bastante común casi todos los conjuntos de datos, sin importar su fuente. No tienen que hacer nada para agregar ruido a las variables, ya está ahí. Los modelos de machine learning lidian con este ruido aproximándose a la forma real de los datos.

Es bastante útil usar la medición del MIC para tener una idea de la información presente en la relación entre dos variables.

1.2.5 Midiendo la no linealidad (MIC-R2)

La función mine devuelve varias métricas, sólo observamos MIC, pero dada la naturaleza del algoritmo (pueden referirse al paper original (Reshef et al. 2011)), puede computar indicadores mucho más interesantes. Pueden examinarlos todos en el objeto res_mine_2.

Uno de ellos es MICR2, que se utiliza como una medida de no linealidad. Se calcula haciendo: MIC - R2. Como R2 mide la linealidad, un alto MICR2 indicaría una relación no lineal.

Podemos verificarlo calculando el MICR2 manualmente, las dos matrices a continuación devuelven el mismo resultado:

# MIC r2: métrica de no linealidad
round(res_mine_2$MICR2, 3)
# Calcular MIC r2 manualmente
round(res_mine_2$MIC-res_R2, 3)

Las relaciones no lineales son más complejas para construir modelos, sobre todo utilizando un algoritmo lineal como árboles de decisión o regresión lineal.

Imaginen que debemos explicar la relación a otra persona, necesitaremos “más palabras” para hacerlo. Es más fácil decir: “A aumenta mientras B disminuye y el coeficiente siempre es 3x” (si A=1 entonces B=3, lineal).

En comparación con: “A aumenta mientras B disminuye, pero A es casi 0 hasta que B alcanza el valor 10, entonces A aumenta a 300; y cuando B alcanza 15, A llega a 1000.”

# Crear un ejemplo con datos
df_example=data.frame(x=df_exp$x, 
                      y_exp=df_exp$y, 
                      y_linear=3*df_exp$x+2)

# Obtener métricas de mine 
res_mine_3=mine(df_example)

# Generar etiquetas para visualizar los resultados
results_linear = 
  sprintf("MIC: %s \n MIC-R2 (non-linearity): %s",
          res_mine_3$MIC[1,3],
          round(res_mine_3$MICR2[1,3],2)
          )

results_exp = 
  sprintf("MIC: %s \n MIC-R2 (non-linearity): %s", 
          res_mine_3$MIC[1,2],
          round(res_mine_3$MICR2[1,2],4)
          )

# Graficar los resultados 
# Crear el gráfico de la variable exponencial
p_exp=ggplot(df_example, aes(x=x, y=y_exp)) + 
  geom_line(color='steelblue') + 
  annotate("text", x = 11, y =0.4, label = results_exp) + 
  theme_minimal()

# Crear el gráfico de la variable lineal
p_linear=ggplot(df_example, aes(x=x, y=y_linear)) + 
  geom_line(color='steelblue') + 
  annotate("text", x = 8, y = 55, 
           label = results_linear) + 
  theme_minimal()

grid.arrange(p_exp,p_linear,ncol=2)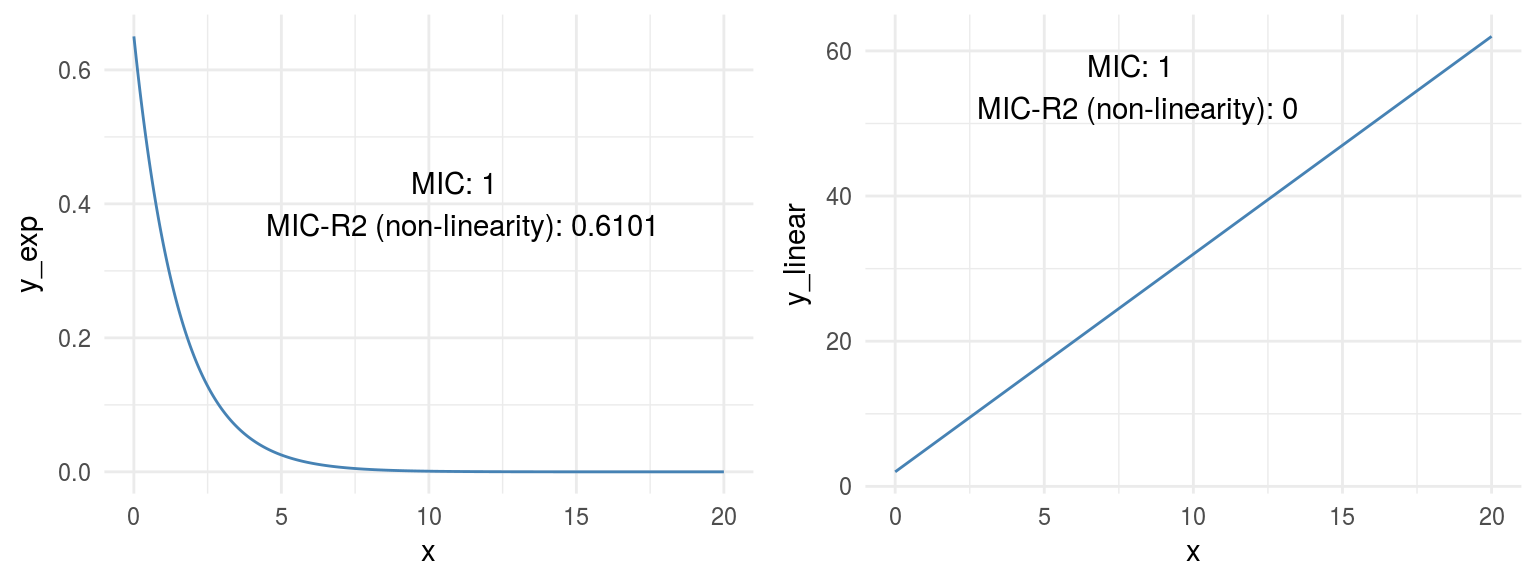

Figure 1.9: Comparando relaciones

Ambos gráficos muestran una correlación (o relación) perfecta, con MIC=1. Con respecto a la no linealidad, MICR2 se comporta como era esperado, en y_exp=0.6101, y en y_linear=0.

Este punto es importante dado que MIC se comporta como R2 en relaciones lineales, además se adapta bastante bien a relaciones no lineales como vimos antes, obteniendo una métrica de puntuación particular (MICR2) para analizar la relación.

1.2.6 Medir información en el Cuarteto de Anscombe

¿Recuerdan el ejemplo que revisamos al principio? Cada par del Cuarteto de Anscombe devuelve un R2 de 0.86. Pero basándonos en los gráficos estaba claro que no todos los pares exhiben ni una buena correlación ni una distribución similar de x y y.

Pero, ¿qué pasa si medimos la relación con una métrica basada en la Teoría de la Información? Sí, otra vez MIC.

# Calcular el MIC para cada par
mic_1=mine(anscombe_data$x1, anscombe_data$y1, alpha=0.8)$MIC
mic_2=mine(anscombe_data$x2, anscombe_data$y2, alpha=0.8)$MIC
mic_3=mine(anscombe_data$x3, anscombe_data$y3, alpha=0.8)$MIC
mic_4=mine(anscombe_data$x4, anscombe_data$y4, alpha=0.8)$MIC

# Graficar el MIC en una cuadrícula 2x2 
grid.arrange(plot_anscombe("x1", "y1", mic_1, "MIC"), plot_anscombe("x2", "y2", mic_2,"MIC"), plot_anscombe("x3", "y3", mic_3,"MIC"), plot_anscombe("x4", "y4", mic_4,"MIC"), ncol=2, nrow=2)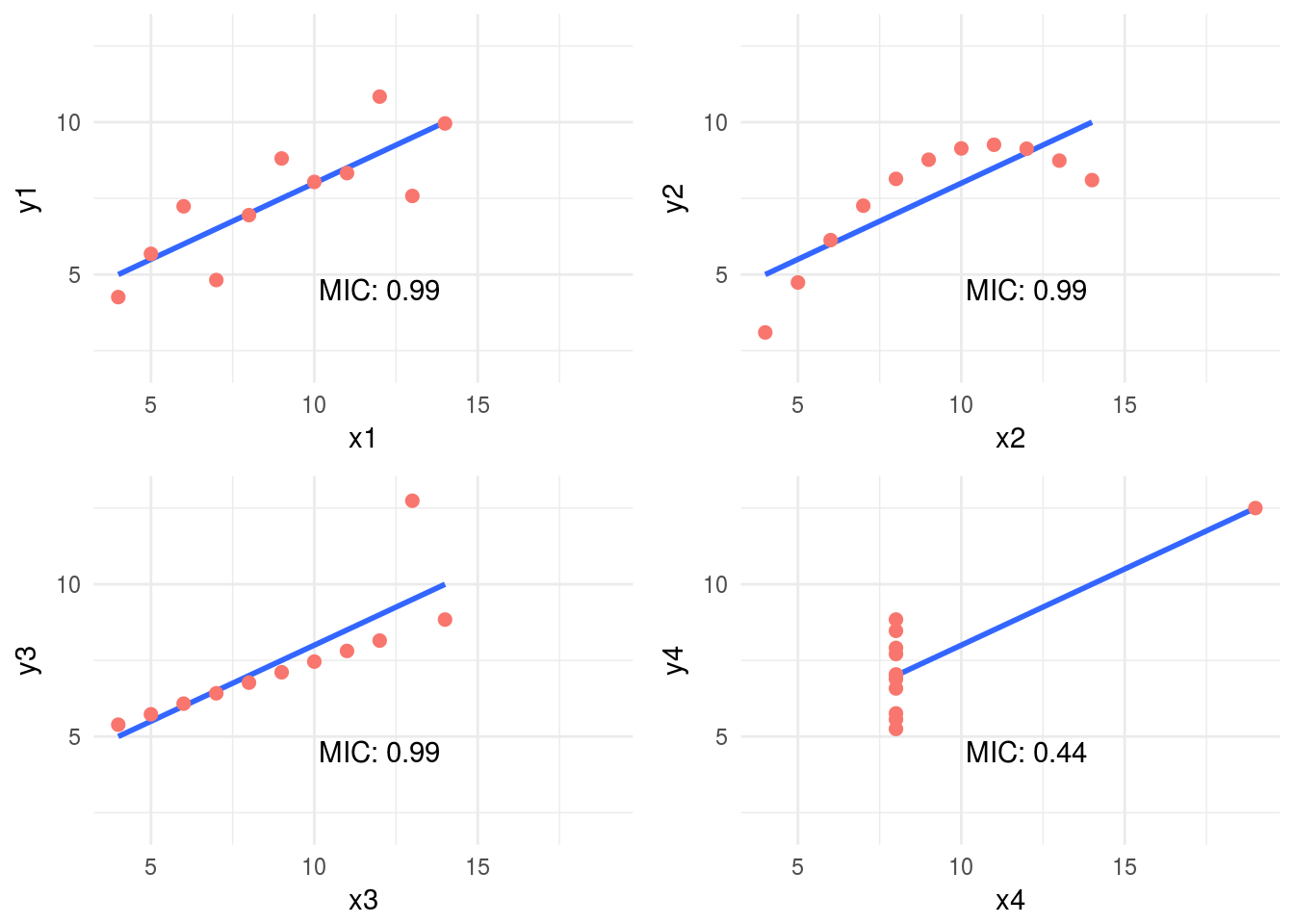

Figure 1.10: Estadístico MIC

Como habrán notado, aumentamos el valor de alpha a 0.8, esto es una buena práctica -de acuerdo a la documentación- cuando analizamos muestras pequeñas. El valor por defecto es 0.6 y el máximo es 1.

En este caso, el valor de MIC detectó la relación más espuria en el par x4 - y4. Probablemente debido a unos pocos casos por gráfico (11 filas) el MIC fue el mismo para todos los otros pares. Tener más casos se reflejará en diferentes valores de MIC.

Pero cuando se combina el MIC con MIC-R2 (medida de no linealidad) aparecen nuevas perspectivas:

# Calcular el MIC para cada par, noten que el objeto "MIC-R2" lleva guión cuando los datos ingresados son dos vectores, a diferencia de las ocasiones en las que toma un data frame, que es "MICR2".
mic_r2_1=mine(anscombe_data$x1, anscombe_data$y1, alpha = 0.8)$`MIC-R2`
mic_r2_2=mine(anscombe_data$x2, anscombe_data$y2, alpha = 0.8)$`MIC-R2`
mic_r2_3=mine(anscombe_data$x3, anscombe_data$y3, alpha = 0.8)$`MIC-R2`
mic_r2_4=mine(anscombe_data$x4, anscombe_data$y4, alpha = 0.8)$`MIC-R2`

# Ordenar por mic_r2
df_mic_r2=data.frame(pair=c(1,2,3,4), mic_r2=c(mic_r2_1,mic_r2_2,mic_r2_3,mic_r2_4)) %>% arrange(-mic_r2)
df_mic_r2

##   pair mic_r2
## 1    2   0.33
## 2    3   0.33
## 3    1   0.33
## 4    4  -0.23

Al ordenarlos de manera decreciente según su no linealidad los resultados son consistentes con los gráficos: 2 > 3 > 1 > 4. Ocurre algo llamativo en el par 4, un número negativo. Esto se debe a que el MIC es inferior al R2. Una relación que merece ser graficada.

1.2.7 Midiendo la no-monotonicidad: medida MAS

MINE también nos puede ayudar a análizar numéricamente series temporales con respecto a su no-monotonicidad con MAS (puntaje de asimetría máxima).

Una serie monótona es aquella que nunca cambia su tendencia, siempre es creciente o decreciente. Encontrarán más información sobre esto en (Wikipedia 2017 b).

El siguiente ejemplo simula dos series temporales, una no-monótona y_1 y una monótona y_2.

# Crear datos de muestra (simulando una serie temporal)
time_x=sort(runif(n=1000, min=0, max=1))
y_1=4*(time_x-0.5)^2
y_2=4*(time_x-0.5)^3

# Calcular el MAS para ambas series
mas_y1=round(mine(time_x,y_1)$MAS,2)
mas_y2=mine(time_x,y_2)$MAS

# Unir todo
df_mono=data.frame(time_x=time_x, y_1=y_1, y_2=y_2)

# Graficar
label_p_y_1 = 
  sprintf("MAS=%s (goes down \n and up => not-monotonic)", 
          mas_y1)

p_y_1=ggplot(df_mono, aes(x=time_x, y=y_1)) + 
  geom_line(color='steelblue') + 
  theme_minimal()  + 
  annotate("text", x = 0.45, y =0.75, 
           label = label_p_y_1)

label_p_y_2=
  sprintf("MAS=%s (goes up => monotonic)", mas_y2)

p_y_2=ggplot(df_mono, aes(x=time_x, y=y_2)) + 
  geom_line(color='steelblue') + 
  theme_minimal() + 
  annotate("text", x = 0.43, y =0.35, 
           label = label_p_y_2)

grid.arrange(p_y_1,p_y_2,ncol=2)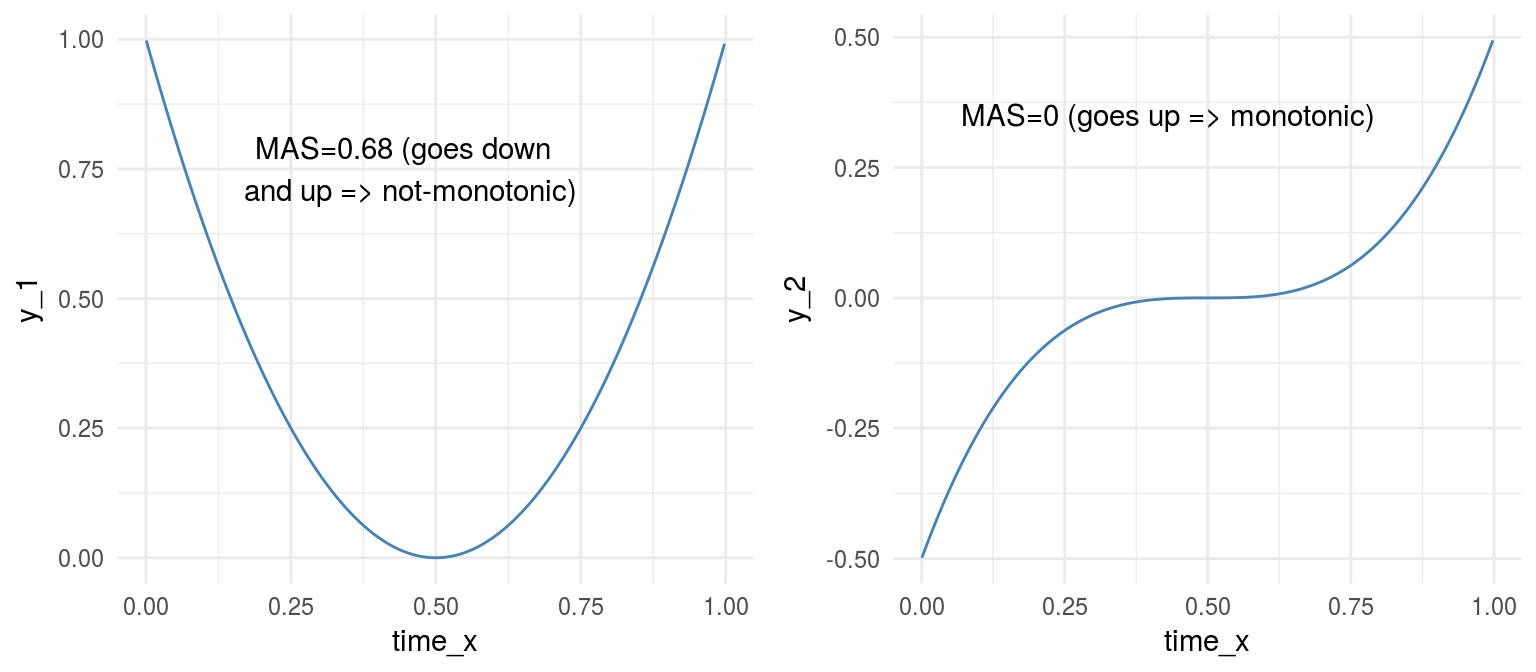

Figure 1.11: Monotonicidad en funciones

Desde otra perspectiva, el MAS también es útil para detectar relaciones periódicas. Ilustremos esto con un ejemplo:

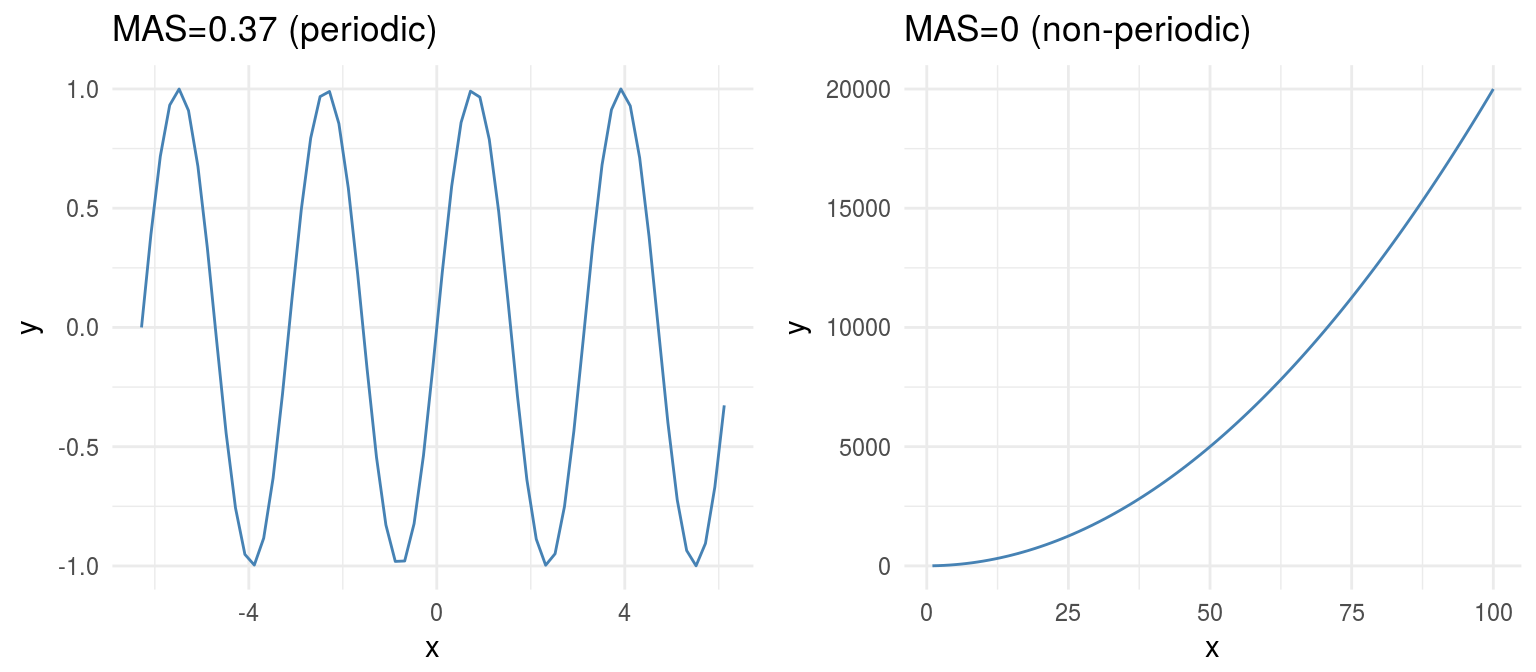
Figure 1.12: Periodicidad en funciones

1.2.7.1 Un ejemplo más real: Series Temporales

Consideren el siguiente caso que contiene tres series temporales: “y1”, “y2” y “y3”. Se pueden analizar numéricamente en cuanto a su no-monotonicidad o a la tendencia general de crecimiento.

# Leer los datos
df_time_series = 
  read.delim(file="https://goo.gl/QDUjfd")

# Convertirlos a formato largo para poder graficarlos
df_time_series_long=melt(df_time_series, id="time")

# Graficar
plot_time_series = 
  ggplot(data=df_time_series_long,
         aes(x=time, y=value, colour=variable)) +
  geom_line() + 
  theme_minimal() + 
  scale_color_brewer(palette="Set2")

plot_time_series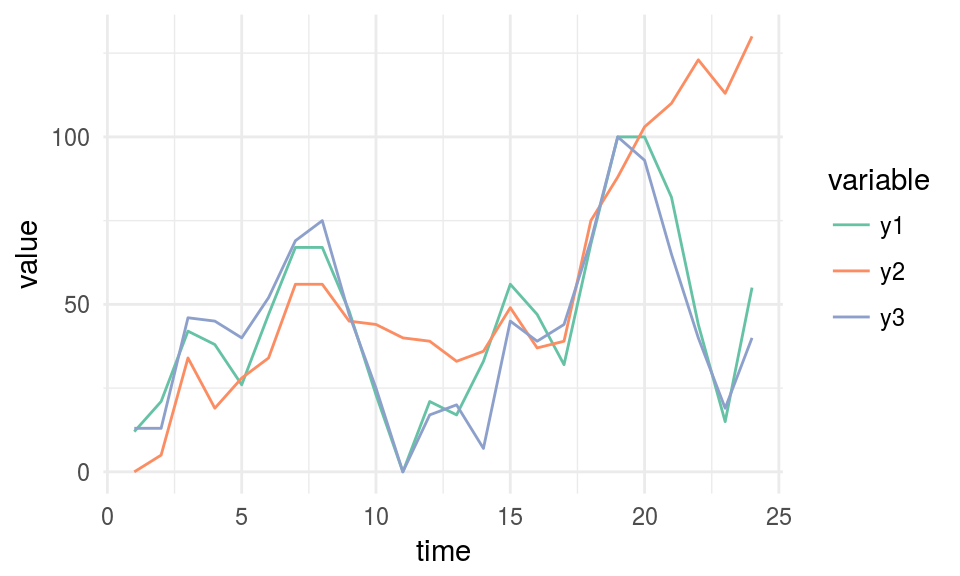

Figure 1.13: Ejemplo de series temporales

# Calcular y visualizar los valores de MAS para datos de series temporales
mine_ts=mine(df_time_series)
mine_ts$MAS

##      time    y1    y2    y3
## time 0.00 0.120 0.105 0.191
## y1   0.12 0.000 0.068 0.081
## y2   0.11 0.068 0.000 0.057
## y3   0.19 0.081 0.057 0.000

Necesitamos mirar la columna de “tiempo”, así tendremos el valor de MAS de cada serie con respecto al tiempo. y2 es la serie más monótona (y menos periódica), y podemos confirmarlo mirándola. Parece que siempre es ascendente.

Resumen de MAS:

MAS ~ 0 indica una función monótona o no periódica (“siempre” ascendente o descendente)
MAS ~ 1 indica una función no-monótona o periódica

1.2.8 Correlación entre series temporales

La métrica MIC también puede medir la correlación en series temporales, no es una herramienta de uso general pero puede ser útil para comparar diferentes series rápidamente.

Esta sección se basa en los mismos datos que usamos en el ejemplo de MAS.

# Visualizar otra vez las 3 series temporales
plot_time_series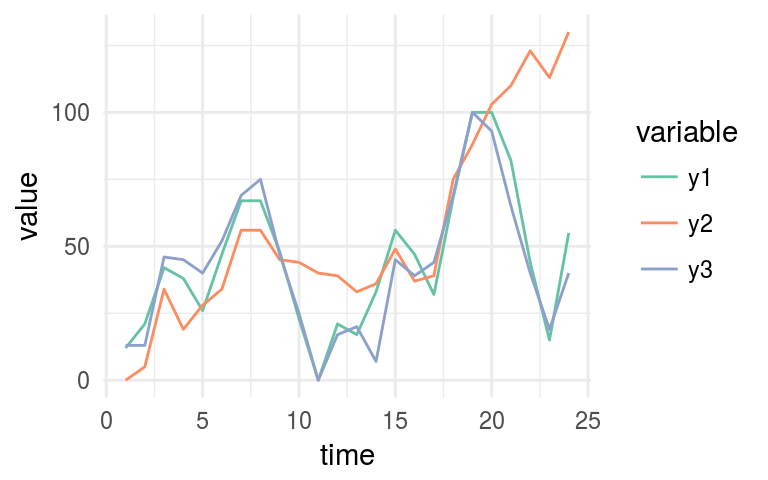

Figure 1.14: Ejemplo de series temporales

# Visualizar los valores de MIC
mine_ts$MIC

##      time   y1   y2   y3
## time 1.00 0.38 0.69 0.34
## y1   0.38 1.00 0.62 0.71
## y2   0.69 0.62 1.00 0.52
## y3   0.34 0.71 0.52 1.00

Ahora tenemos que mirar la columna y1. De acuerdo con la medición del MIC, podemos confirmar lo mismo que se muestra en el último gráfico:

y1 es más parecido a y3 (MIC=0.709) que a y2 (MIC=0.61).

1.2.8.1 Yendo más allá: Deformación dinámica del tiempo

El MIC no servirá en escenarios más complejos que tengan series temporales que varíen en velocidad, utilizaremos la técnica de [deformación dinámica del tiempo] (https://en.wikipedia.org/wiki/Dynamic_time_warping) (DTW, en inglés).

Usemos una imagen para acercarnos al concepto visualmente:

Figure 1.15: Deformación dinámica del tiempo

Fuente de la imagen: Deformación dinámica del tiempo Convirtiendo imágenes en series temporales para data mining (Izbicki 2011).

La última imagen muestra dos enfoques diferentes para comparar series temporales, y el euclídeo es más similar a la medición del MIC. Mientras que la Deformación dinámica del tiempo puede rastrear las similitudes que ocurren en diferentes momentos.

Una linda implementación en R: dtw package.

Encontrar correlaciones entre series temporales es otra forma de agrupar series temporales.

1.2.9 Correlación en variables categóricas

MINE -y muchos otros algoritmos- sólo funcionan con datos numéricos. Tenemos que hacer un truco de preparación de datos, convirtiendo cada variable categórica en un flag (o variable dummy).

Si la variable categórica original tiene 30 valores posibles, como resultado tendremos 30 nuevas columnas con valor 0 o 1, donde 1 representa la presencia de esa categoría en la fila.

Si usamos el paquete caret de R, esta conversión sólo requiere dos líneas de código:

library(caret)

# Seleccionar sólo algunas variables
heart_disease_2 = 
  select(heart_disease, max_heart_rate, oldpeak, 
         thal, chest_pain,exer_angina, has_heart_disease)

# Esta conversión de categórica a numérica es meramente para 
# tener un gráfico más limpio
heart_disease_2$has_heart_disease=
  ifelse(heart_disease_2$has_heart_disease=="yes", 1, 0)

# Convierte todas las variables categóricas (factor y 
# carácter para R) en variables numéricas
# saltando las originales para que los datos estén
# listos para usar
dmy = dummyVars(" ~ .", data = heart_disease_2)

heart_disease_3 = 
  data.frame(predict(dmy, newdata = heart_disease_2))

# Importante: Si ven este mensaje
# `Error: Missing values present in input variable 'x'. 
# Consideren usar = 'pairwise.complete.obs'.` 
# Es porque los datos tienen valores faltantes.
# Por favor no omitan valores NA sin analizar el
# impacto antes, en este caso no es importante. 
heart_disease_4=na.omit(heart_disease_3)
  
# ¡Computen el mic!
mine_res_hd=mine(heart_disease_4)

Visualizando una muestra…

mine_res_hd$MIC[1:5,1:5]

##                max_heart_rate oldpeak thal.3 thal.6 thal.7
## max_heart_rate           1.00    0.24  0.244  0.120  0.184
## oldpeak                  0.24    1.00  0.175  0.111  0.157
## thal.3                   0.24    0.18  0.992  0.073  0.710
## thal.6                   0.12    0.11  0.073  0.327  0.044
## thal.7                   0.18    0.16  0.710  0.044  0.964

Donde la columna thal.3 toma un valor de 1 cuando thal=3.

1.2.9.1 ¡Visualizamos unos sofisticados gráficos!

Utilizaremos el paquete corrplot de R que puede graficar un objeto cor (matriz de correlación clásica), o cualquier otra matriz. Graficaremos la matriz MIC en este caso, pero también se puede usar cualquier otra, por ejemplo, MAS o cualquier otra métrica que devuelva una matriz cuadrada de correlaciones.

Los dos gráficos se basan en los mismos datos pero muestran la correlación de distintas formas.

# Biblioteca para graficar esta matriz
library(corrplot) 
# Para usar la paleta de color brewer.pal
library(RColorBrewer) 

# Truco para visualizar el valor máximo de la escala
# excluyendo la diagonal (var. con respecto a sí misma)
diag(mine_res_hd$MIC)=0

# Gráfico de correlación con círculos. 
corrplot(mine_res_hd$MIC, 
         method="circle",
         col=brewer.pal(n=10, name="PuOr"),
         # Mostrar sólo la diagonal superior
         type="lower", 
         #color, tamaño y rotación de las etiquetas
         tl.col="red",
         tl.cex = 0.9, 
         tl.srt=90, 
         # no visualizar la diagonal,
         # (var con respecto a sí misma)
         diag=FALSE, 
         # aceptar cualquier matriz, mic en este caso
         #(no es un elemento de correlación)
         is.corr = F 
        
)

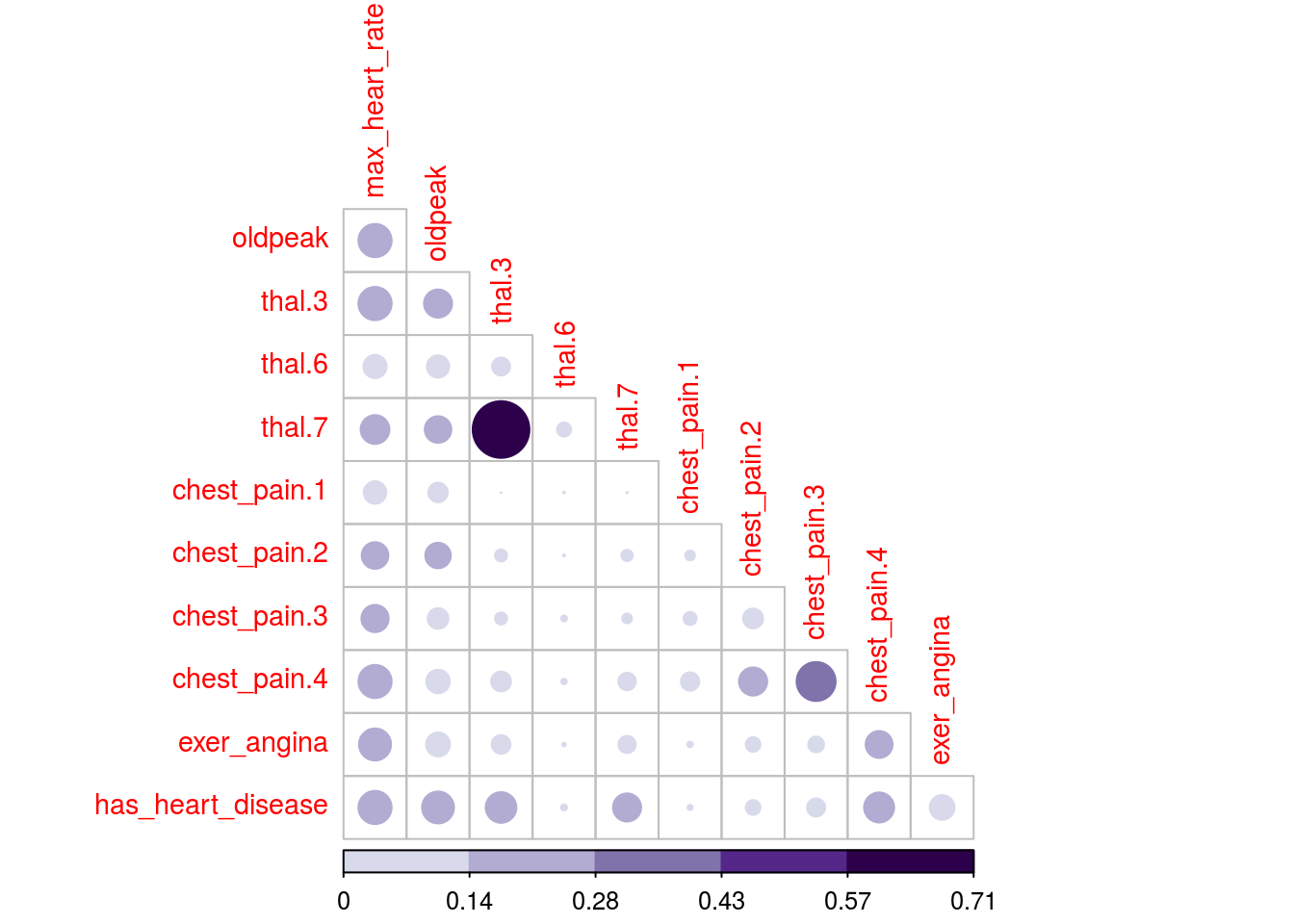
Figure 1.16: Gráfico de correlación

# Gráfico de correlación con color y correlación MIC
corrplot(mine_res_hd$MIC, 
         method="color",
         type="lower", 
         number.cex=0.7,
         # Agregar coeficiente de correlación
         addCoef.col = "black", 
         tl.col="red", 
         tl.srt=90, 
         tl.cex = 0.9,
         diag=FALSE, 
         is.corr = F 
)

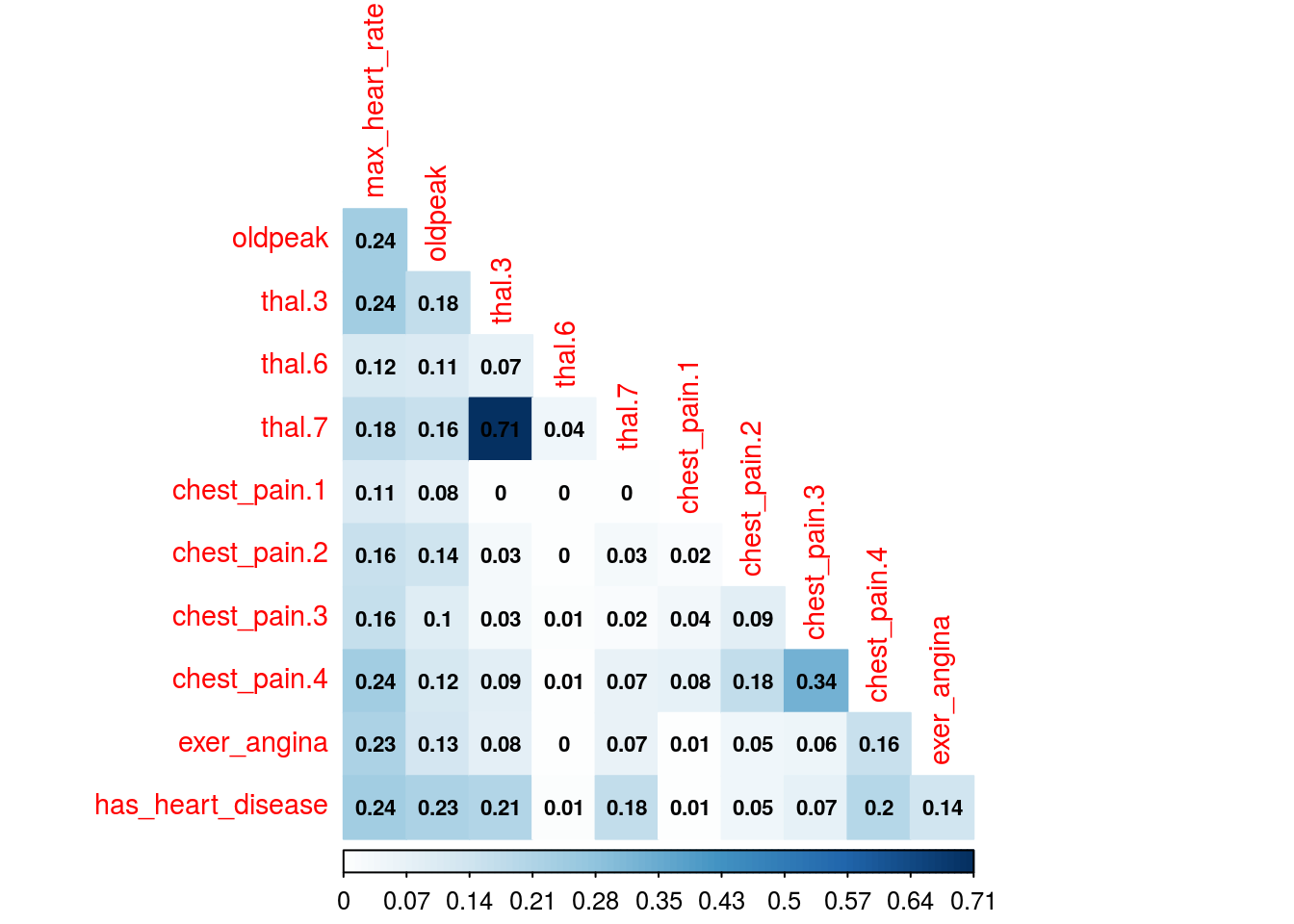
Figure 1.16: Gráfico de correlación

Simplemente cambien el primer parámetro -mine_res_hd$MIC- a la matriz que quieran y reutilicen el código con sus datos.

1.2.9.2 Un comentario sobre este tipo de gráficos

Sólo son útiles cuando no hay un gran número de variables. O si primero hacen una selección de variables, teniendo en cuenta que todas deben ser numéricas.

Si hay alguna variable categórica en la selección, pueden convertirla primero en numérica e inspeccionar la relación entre las variables, para ver cómo ciertos valores de las variables categóricas están más relacionados con ciertos resultados, como en este caso.

1.2.9.3 ¿Qué tal si sacamos algunas conclusiones de los gráficos?

Como la variable a predecir es has_heart_disease, aparece algo interesante: tener una enfermedad cardíaca está más correlacionado con thal=3 que con el valor thal=6.

El mismo análisis aplica para la variable `chest_pain’, un valor de 4 es más peligroso que un valor de 1.

Y podemos comprobarlo con otro gráfico:

cross_plot(heart_disease, input = "chest_pain", target = "has_heart_disease", plot_type = "percentual")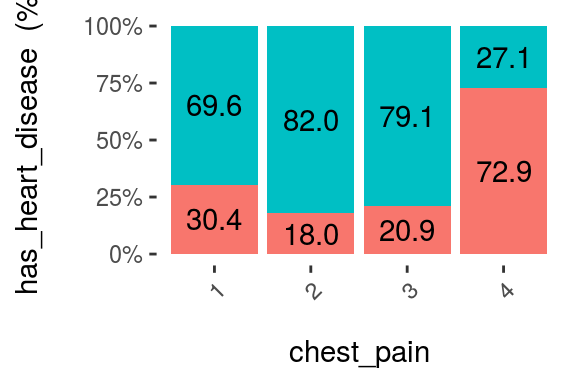

Figure 1.17: Análisis visual utilizando cross-plot

La probabilidad de tener una enfermedad cardíaca es del 72,9% si el paciente tiene dolor en el pecho=4. Más de 2 veces más probable que si tiene dolor_en_el_pecho=1 (72.9 vs 30.4%).

Algunas reflexiones…

Los datos son los mismos, pero el enfoque para explorarlos es diferente. Lo mismo ocurre cuando estamos creando un modelo predictivo, los datos ingresados en el espacio N-dimensional pueden ser abordados mediante diferentes modelos, como: Máquinas de vectores soporte (support vector machine o SVM, en inglés), Bosques aleatorios (random forests), etc.

Como un fotógrafo que dispara desde diferentes ángulos o desde diferentes cámaras. El objeto es siempre el mismo, pero la perspectiva brinda información diferente.

La combinación de tablas en crudo y diferentes gráficos nos da una perspectiva de objeto más real y complementaria.

1.2.10 Análisis de correlación basado en la Teoría de la Información

Basándose en la medición del MIC, la función mine puede recibir el índice de la columna a predecir (o para obtener todas las correlaciones contra una sola variable).

# Obtener el índice de la variable a 
# predecir: has_heart_disease
target="has_heart_disease"
index_target=grep(target, colnames(heart_disease_4))

# master toma el número de la columna índice para
# calcular todas las correlaciones
mic_predictive=mine(heart_disease_4, 
                    master = index_target)$MIC

# Crear el data frame que contiene los resultados,
# ordenándolos por correlación decreciente y excluyendo
# la correlación del objetivo con respecto a sí mismo
df_predictive = 
  data.frame(variable=rownames(mic_predictive), 
                         mic=mic_predictive[,1], 
                         stringsAsFactors = F) %>% 
  arrange(-mic) %>% 
  filter(variable!=target)

# Crear un colorido gráfico que muestre la 
# importancia de las variables basándonos en
# la medición del MIC
ggplot(df_predictive, 
       aes(x=reorder(variable, mic),y=mic, fill=variable)
       ) + 
  geom_bar(stat='identity') + 
  coord_flip() + 
  theme_bw() + 
  xlab("") + 
  ylab("Variable Importance (based on MIC)") + 
  guides(fill=FALSE)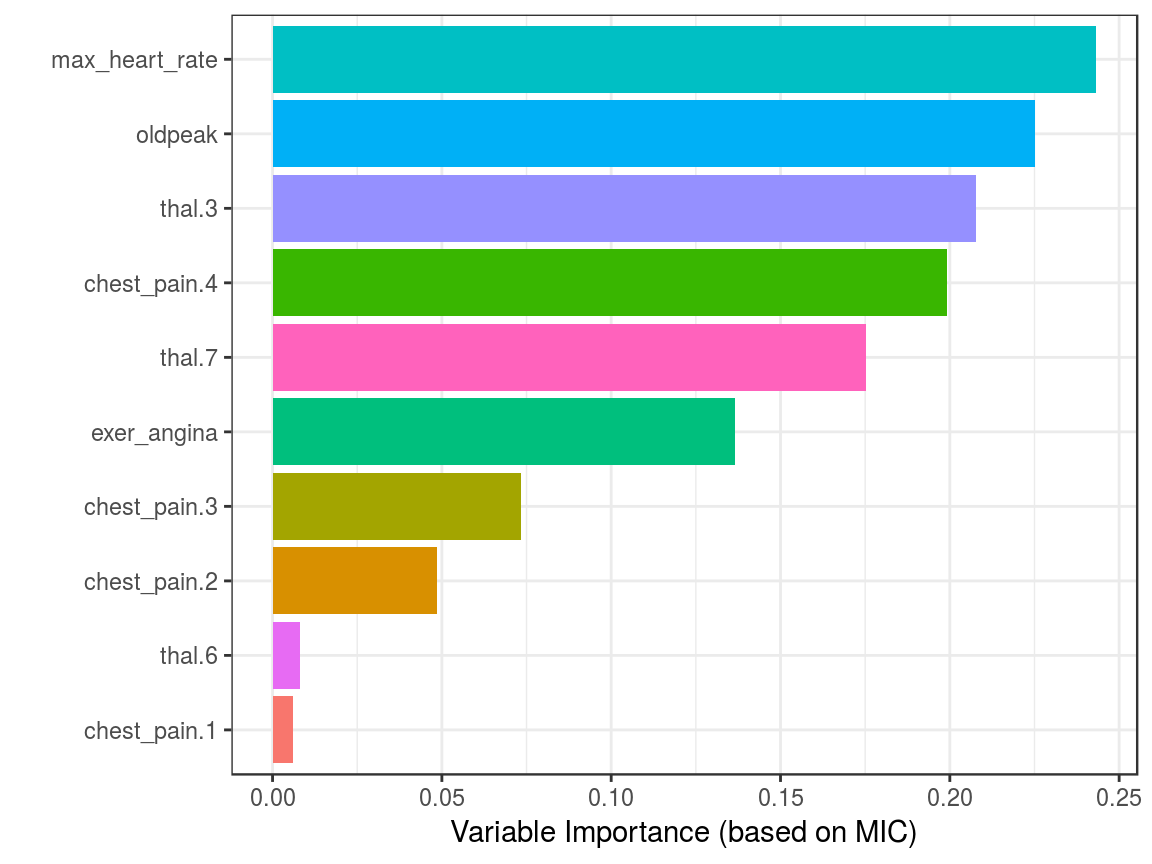

Figure 1.18: Correlación utilizando la Teoría de la Información

Aunque es recomendable ejecutar las correlaciones entre todas las variables para excluir factores ingresados correlacionados.

1.2.10.1 Consejos prácticos al utilizar `mine`

Si lleva demasiado tiempo, consideren tomar una muestra. Si hay muy pocos datos, consideren utilizar un valor más alto en el parámetro alpha, 0.6 es el valor por defecto. También se puede ejecutar en paralelo, configurando el parámetro n.cores=3 si tienen 4 cores. Una buena práctica en general cuando se ejecutan procesos paralelos, el core extra será utilizado por el sistema operativo.

1.2.11 ¿Sólo MINE cubre esto?

No. Sólo usamos la suite de MINE, pero hay otros algoritmos relacionados con información mutua. En R algunos de los paquetes son: entropy y infotheo.

El paquete funModeling (desde la versión 1.6.6) introduce la función var_rank_info, que calcula varias métricas de la Teoría de la Información, como vimos en la sección Análisis de correlación basado en la Teoría de la Información.

En Python se puede calcular información mutua mediante scikit-learn, aquí un ejemplo.

El concepto trasciende la herramienta.

1.2.11.1 Otro ejemplo de correlación (información mutua)

Esta vez utilizaremos el paquete infotheo. Primero tenemos que hacer un un paso de preparación de datos, aplicando una función discretize (o de binning) que está incluida en el paquete. Convierte todas las variables numéricas a categóricas basándose en criterios de igual frecuencia.

El siguiente código creará la matriz de correlación como hemos visto antes, pero basándose en el índice de información mutua:

library(infotheo)
# Discretizar cada variable
heart_disease_4_disc=discretize(heart_disease_4) 

# Calcular la "correlación" basándonos en información mutua
heart_info=mutinformation(heart_disease_4_disc, method= "emp")

# Truco para visualizar el valor máximo de la escala
# excluyendo la diagonal (variable con respecto a sí misma)
diag(heart_info)=0

# Gráfico de correlación con color y correlación con información mutua del paquete Infotheo. Esta línea sólo obtiene el gráfico de la derecha.
corrplot(heart_info, method="color",type="lower", number.cex=0.6,addCoef.col = "black", tl.col="red", tl.srt=90, tl.cex = 0.9, diag=FALSE, is.corr = F)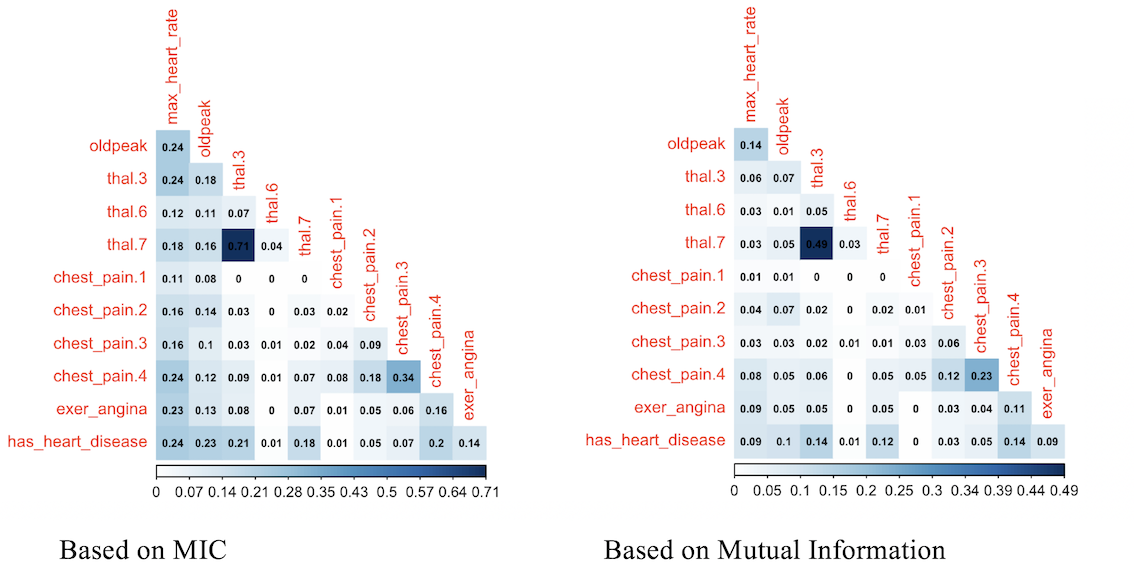

Figure 1.19: Comparando la importancia de las variables

El puntaje de correlación basado en información mutua ordena las relaciones de una forma bastante similar al MIC, ¿no es cierto?

1.2.12 Medidas de información: Una perspectiva general

Más allá de la correlación, MIC y otras medidas de información identifican si hay una relación funcional.

Un alto MIC indica que la relación entre las dos variables puede explicarse por una función. Es nuestro trabajo encontrar esa función o modelo predictivo.

Este análisis se extiende a n-variables, este libro introduce otro algoritmo en el capítulo de Selección de las mejores variables.

Algunos modelos predictivos funcionan mejor que otros, pero si la relación es absolutamente ruidosa, sin importar cuán avanzado sea el algoritmo, los resultados serán malos.

Hay mucho más sobre la Teoría de la Información más adelante. Por ahora, pueden investigar estas lecturas didácticas:

Video introductorio de 7 minutos https://www.youtube.com/watch?v=2s3aJfRr9gE
http://alex.smola.org/teaching/cmu2013-10-701x/slides/R8-information_theory.pdf
http://www.scholarpedia.org/article/Mutual_information

1.2.13 Conclusiones

El Cuarteto de Anscombe nos enseñó la buena práctica de combinar la estadística cruda con un gráfico.

Pudimos ver cómo el ruido puede afectar la relación entre dos variables, y este fenómeno siempre aparece en los datos. El ruido en los datos confunde al modelo predictivo.

El ruido está relacionado con el error, y puede ser estudiado con medidas basadas en la Teoría de la Información, tales como información mutua y MIC, que van un paso más allá de la típica R cuadrado. Existe un estudio clínico que utiliza MINE como selector de características en(Caban et al. 2012).

Estos métodos son aplicables en ingeniería de factores como un método que no se basa en un modelo predictivo para clasificar las variables más importantes. También se aplica a las series temporales agrupadas.

Siguiente capítulo recomendado: Selección de las mejores variables

Referencias

McNeese, Bill. 2016. “Are the Skewness and Kurtosis Useful Statistics?” https://www.spcforexcel.com/knowledge/basic-statistics/are-skewness-and-kurtosis-useful-statistics.

Handbook, Engineering Statistics. 2013. “Measures of Skewness and Kurtosis.” http://www.itl.nist.gov/div898/handbook/eda/section3/eda35b.htm.

Reshef, David N., Yakir A. Reshef, Hilary K. Finucane, Sharon R. Grossman, Gilean McVean, Peter J. Turnbaugh, Eric S. Lander, Michael Mitzenmacher, and Pardis C. Sabeti. 2011. “Detecting Novel Associations in Large Data Sets.” Science 334 (6062): 1518–24. doi:10.1126/science.1205438.

Wikipedia. 2017b. “Monotonic Function.” https://en.wikipedia.org/wiki/Monotonic_function.

Izbicki, Mike. 2011. “Converting Images into Time Series for Data Mining.” https://izbicki.me/blog/converting-images-into-time-series-for-data-mining.html.

Caban, Jesus J., Ulas Bagci, Alem Mehari, Shoaib Alam, Joseph R. Fontana, Gregory J. Kato, and Daniel J. Mollura. 2012. “Characterizing Non-Linear Dependencies Among Pairs of Clinical Variables and Imaging Data.” Conf Proc IEEE Eng Med Biol Soc 2012 (August): 2700–2703. doi:10.1109/EMBC.2012.6346521.