3 Selección de las mejores variables
3.1 Aspectos generales de la selección de las mejores variables
3.1.1 ¿De qué se trata esto?
Este capítulo abarca los siguientes temas:
- El ranking de mejores variables según los algoritmos convencionales de machine learning, ya sean predictivos o de agrupamiento.
- La naturaleza de la selección de variables con y sin modelos predictivos.
- El efecto de las variables trabajando en grupos (intuición y Teoría de la Información).
- Explorar el mejor subconjunto de variables en la práctica usando R.
La selección de las mejores variables también se conoce como selección de los predictores más importantes, selección de los mejores predictores, entre otros.

Figure 3.1: Como es arriba, es abajo
Image: ¿Es una red neuronal? Nop. Materia oscura, de “The Millennium Simulation Project”.
3.2 Intuición
Seleccionar las mejores variables es como hacer un resumen de una historia, queremos concentrarnos en unos pocos detalles que mejor describen lo que estamos contando. El equilibrio está entre hablar demasiado sobre detalles innecesarios (sobreajustar/overfitting) y hablar muy poco sobre la esencia de la historia (subajustar/underfitting).
Otro ejemplo puede ser la decisión de comprar una nueva computadora portátil: ¿cuáles son los factores que más nos importan? ¿Precio, color y forma de envío? ¿Color y duración de la batería? ¿O sólo precio?
Desde el punto de vista de la Teoría de la Información -un punto clave en machine learning-, los datos con los que estamos trabajando tienen entropía (caos). Cuando seleccionamos variables, estamos disminuyendo la entropía en nuestro sistema agregando información.
3.3 ¿La “mejor” selección?
Este capítulo dice “las mejores”, pero conviene que mencionemos un punto conceptual: en términos generales, no hay una única selección de mejores variables.
Partir de esta perspectiva es importante dado que, en la exploración de muchos algoritmos que clasifican las variables según su poder predictivo, podemos encontrar resultados diferentes -y similares-. Por ejemplo:
- El algoritmo 1 seleccionó
var_1como la mejor variable, seguida devar_5yvar_14. - El algoritmo 2 hizo este ranking:
var_1,var_5yvar_3.
Imaginemos, basándonos en el algoritmo 1, que la precisión es del 80%, mientras que la precisión al basarnos en el algoritmo 2 es del 78%. Considerando que cada modelo tiene su propia varianza interna, los resultados pueden ser vistos como iguales.
Esta perspectiva nos puede ayudar a reducir el tiempo que nos lleva buscar la selección perfecta de variables.
No obstante, yendo a los extremos, sí habrá un conjunto de variables que tendrá una alta clasificación en muchos algoritmos, y lo mismo aplica para aquellas con bajo poder predictivo. Después de varias ejecuciones, las variables más confiables saldrán rápidamente a la luz, entonces:
Conclusión: Si los resultados no son buenos, deberíamos enfocarnos en mejorar y revisar la instancia de preparación de datos. La siguiente sección dará un ejemplo de esto.
3.3.1 Profundizando en la clasificación de variables
Es bastante común encontrar en literatura y algoritmos que cubren este tema un análisis univariado, que es un ranking de variables según una métrica particular.
Vamos a crear dos modelos: random forest y gradient boosting machine (GBM) usando el paquete caret en R para hacer una verificación cruzada de los datos. Luego, vamos a comparar el ranking de mejores variables que devuelva cada modelo.
library(caret)
library(funModeling)
library(dplyr)
# Excluir todas las filas NA de los datos, en este caso, los NA no son el principal problema a resolver, por lo que omitiremos los 6 casos que tienen NA (o valores faltantes).
heart_disease=na.omit(heart_disease)
# Configurar una validación cruzada cuádruple
fitControl = trainControl(method = "cv",
number = 4,
classProbs = TRUE,
summaryFunction = twoClassSummary)
# Crear el modelo de random forest, encontrando el mejor conjunto de parámetros de ajuste
set.seed(999)
fit_rf = train(x=select(heart_disease, -has_heart_disease, -heart_disease_severity),
y = heart_disease$has_heart_disease,
method = "rf",
trControl = fitControl,
verbose = FALSE,
metric = "ROC")
# Crear el modelo de gradient boosting machine, encontrando el mejor conjunto de parámetros de ajuste
fit_gbm = train(x=select(heart_disease, -has_heart_disease, -heart_disease_severity),
y = heart_disease$has_heart_disease,
method = "gbm",
trControl = fitControl,
verbose = FALSE,
metric = "ROC")Ahora podemos proceder a la comparación.
Las columnas importance_rf y importance_gbm representan la importancia medida por cada algoritmo. De acuerdo a cada métrica, existen rank_rf y rank_gbm, que representan el orden de importancia. Finalmente, rank_diff (rank_rf - rank_gbm) representa cuán diferentes son los rankings de los algoritmos.
# Aquí manipulamos para mostrar una linda tabla con lo que describimos arriba
var_imp_rf=data.frame(varImp(fit_rf, scale=T)["importance"]) %>%
dplyr::mutate(variable=rownames(.)) %>% dplyr::rename(importance_rf=Overall) %>%
dplyr::arrange(-importance_rf) %>%
dplyr::mutate(rank_rf=seq(1:nrow(.)))
var_imp_gbm=as.data.frame(varImp(fit_gbm, scale=T)["importance"]) %>%
dplyr::mutate(variable=rownames(.)) %>% dplyr::rename(importance_gbm=Overall) %>%
dplyr::arrange(-importance_gbm) %>%
dplyr::mutate(rank_gbm=seq(1:nrow(.)))
final_res=merge(var_imp_rf, var_imp_gbm, by="variable")
final_res$rank_diff=final_res$rank_rf-final_res$rank_gbm
# ¡Visualizar los resultados!
final_res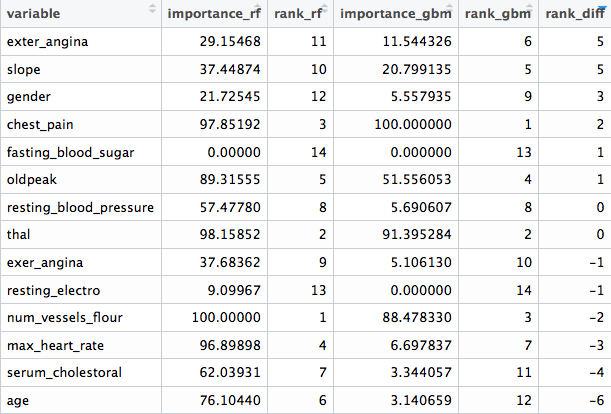
Figure 3.2: Comparación de diferentes clasificaciones de variables
Podemos ver que hay variables que no son para nada importantes en ambos modelos (fasting_blood_sugar). Hay otras que mantienen una posición en lo más alto del ranking de importancia, como chest_pain y thal.
Las implementaciones de diferentes modelos predictivos tienen sus propios criterios para informar cuáles son los mejores factores, de acuerdo a ese modelo particular. Esto resulta en diferentes clasificaciones en los diferentes algoritmos. Hay más información sobre la importancia de las métricas internas en la documentación de caret.
Además, en los modelos basados en árboles, como GBM y random forest, hay un componente aleatorio en la selección de variables, y la importancia se basa en una selección anterior -y automática- a la hora de construir los árboles. La importancia de cada variable depende de las otras, no solamente en su contribución aislada: Las variables trabajan en grupos. Regresaremos a este punto más adelante en este capítulo.
Si bien el ranking variará de algoritmo a algoritmo, en términos generales suele haber una correlación entre todos estos resultados, como mencionamos previamente.
Conclusión: Cada lista de clasificación de variables no es la “verdad final”, nos orienta sobre dónde está la información.
3.4 La naturaleza de la selección
Hay dos principales enfoques a la hora de seleccionar variables:
Dependiente de los modelos predictivos:
Como los ejemplos que vimos antes, este es el más común. El modelo ordenará las variables de acuerdo a una medida intrínseca de precisión. En los modelos basados en árboles, métricas como ganancia de información, índice de Gini, impureza de nodos. Hay más información sobre esto en (stackoverflow.com 2017) y (stats.stackexchange.com 2017a).
No dependiente de los modelos predictivos:
Los criterios de este tipo son interesantes dado que no son tan populares como los otros, pero se ha comprobado que funcionan muy bien en áreas relacionadas con datos genómicos. Deben encontrar aquellos genes relevantes (variable de entrada) que están correlacionados con alguna enfermedad, como cáncer (variable objetivo).
Los datos de esta área de estudio se caracterizan por tener una enorme cantidad de variables (miles), que es mucho mayor a los problemas que abordan otras áreas.
Un algoritmo para lograr esto es mRMR, acrónimo de Selección de Factores con Mínima Redundancia y Máxima Relevancia (Minimum Redundancy Maximum Relevance Feature Selection en inglés). Tiene su propia implementación en R en el paquete mRMRe.
Otro algoritmo no dependiente de modelos es var_rank_info, una función incluida en el paquete funModeling. Clasifica las variables usando varias métricas de Teoría de la Información. Presentaremos un ejemplo más adelante.
3.5 Mejorar variables
Podemos aumentar el poder predictivo de las variables tratándolas.
Hasta aquí, este libro ha cubierto:
- Mejora de variables categóricas.
- Reducción de ruido en variables numéricas mediante agrupación en el capítulo: Discretizando variables numéricas.
- Cómo lidiar con valores atípicos en R.
- Análisis, manejo e imputación
3.6 Limpiar por conocimiento del dominio
Esto no está relacionado con procedimientos algorítmicos, sino con el área de donde vienen los datos.
Imaginen que los datos vienen de una encuesta. Esta encuesta tiene un año de historia, y durante los primeros tres meses no hubo un buen control del proceso. Al ingresar los datos, los usuarios podían escribir lo que quisieran. Las variables durante este período probablemente serán espurias.
Es fácil reconocerlo cuando durante un período de tiempo dado la variable viene vacía, nula o con valores extremos.
Entonces deberíamos hacer una pregunta:
¿Estos datos son confiables? Tengan en cuenta que el modelo predictivo aprenderá como un niño, no juzgará los datos, solo aprenderá de ellos. Si los datos son espurios en un período de tiempo determinado, entonces podemos eliminar estos casos ingresados.
Para avanzar más en este punto, deberíamos hacer un análisis exploratorio más profundo de los datos. Tanto numérica como gráficamente.
3.7 Las variables trabajan en grupos
Figure 3.3: Las variables trabajan en grupos
Cuando seleccionamos las mejores variables, el principal objetivo es obtener aquellas variables que contienen la mayor información con respecto a una variable objetivo, de resultado o dependiente.
Un modelo predictivo encontrará sus pesos o parámetros basándose en sus 1 a ‘N’ variables de ingreso.
Las variables aisladas no suelen funcionar para explicar un evento. Citando a Aristóteles:
“El todo es más que la suma de las partes.”
Esto también aplica cuando queremos seleccionar las mejores variables:
Construir un modelo predictivo con dos variables puede brindar una mayor precisión que los modelos construidos con una sola variable.
Por ejemplo: Construir un modelo basado en la variable var_1 podría llevarnos a una precisión global del 60%. Por otro lado, un modelo basado en var_2 podría alcanzar una precisión del 72%. Pero al combinar estas dos variables, var_1 y var_2 variables, podríamos lograr una precisión que supere el 80%.
3.7.1 Ejemplo en R: Variables trabajando en grupos

Figure 3.4: Aristóteles (384 a.C.–322 a.C.)
El siguiente código ilustra lo que Aristóteles dijo hace algunos años.
Crea 3 modelos basados en diferentes subconjuntos de variables:
- El modelo 1 está basado en la variable de entrada
max_heart_rate - El modelo 2 está basado en la variable de entrada
chest_pain - El modelo 3 está basado en las variables de entrada
max_heart_rateychest_pain
Cada modelo devuelve la métrica ROC, y el resultado contiene la mejora de considerar dos variables al mismo tiempo vs. tomar cada variable por separado.
library(caret)
library(funModeling)
library(dplyr)
# Configurar la validación cruzada 4-fold
fitControl =
trainControl(method = "cv",
number = 4,
classProbs = TRUE,
summaryFunction = twoClassSummary
)
create_model<-function(input_variables)
{
# Crear el modelo de gradient boosting machine
# basado en las variables de entrada
fit_model = train(x=select(heart_disease,
one_of(input_variables)
),
y = heart_disease$has_heart_disease,
method = "gbm",
trControl = fitControl,
verbose = FALSE,
metric = "ROC")
# Devolver el ROC como una métrica de desempeño
max_roc_value=max(fit_model$results$ROC)
return(max_roc_value)
}
roc_1=create_model("max_heart_rate")
roc_2=create_model("chest_pain")
roc_3=create_model(c("max_heart_rate", "chest_pain"))
avg_improvement=round(100*(((roc_3-roc_1)/roc_1)+
((roc_3-roc_2)/roc_2))/2,
2)
avg_improvement_text=sprintf("Average improvement: %s%%",
avg_improvement)
results =
sprintf("ROC model based on 'max_heart_rate': %s.;
based on 'chest_pain': %s; and based on both: %s",
round(roc_1,2),
round(roc_2,2),
round(roc_3, 2)
)
# ¡Visualizar los resultados!
cat(c(results, avg_improvement_text), sep="\n\n")## ROC model based on 'max_heart_rate': 0.71.;
## based on 'chest_pain': 0.77; and based on both: 0.81
##
## Average improvement: 9.9%3.7.2 Pequeño ejemplo (basado en la Teoría de la información)
Consideren la siguiente tabla de big data 😜 4 filas, 2 variables de entrada (var_1, var_2) y un resultado (target):
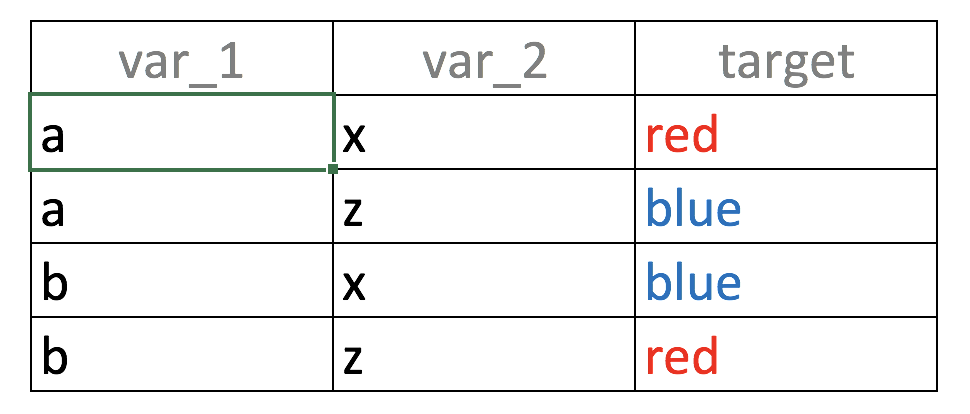
Figure 3.5: La unión hace a la fuerza: Combinar variables
Si creamos un modelo predictivo basado solamente en var_1, ¿qué verá este modelo?, el valor a está correlacionado con el resultado blue y red en la misma proporción (50%):
- Si
var_1='a'entonces la probabilidad del objetivo=‘red’ es 50% (fila 1) - Si
var_1='b'entonces la probabilidad del objetivo=‘blue’ es 50% (fila 2)
El mismo análisis aplica para var_2
Cuando los mismos datos ingresados están relacionados con diferentes resultados lo definimos como ruido. La intuición es lo mismo que una persona diciéndonos: “Hey, ¡mañana va a llover!”, y otra persona diciéndonos “Es seguro que mañana no va a llover”. Pensaríamos… “¡Dios mío! ¿Necesito el paraguas o no 😱?”
Volviendo al ejemplo, al tomar las dos variables en simultáneo, la correspondencia entre los datos ingresados y el resultado es única: “Si var_1='a' y var_2='x' entonces la probabilidad de target='red' es 100%”. Pueden probar otras combinaciones.
Resumiendo:
Ese fue un ejemplo de variables trabajando en grupos, considerar var_1 y var_2 al mismo tiempo aumenta el poder predictivo.
No obstante, es un tema más profundo para tratar, teniendo en cuenta el último análisis; ¿qué pasa si tomamos una columna Id (cada valor es único) para predecir algo? La correspondencia entre datos ingresados y resultado también será única… ¿pero es un modelo útil? Hablaremos más sobre Teoría de la Información en este libro.
3.7.3 Conclusiones
- El ejemplo en R que propusimos, basado en los datos de
heart_disease, muestra en promedio una mejora del 9% al considerar dos variables al mismo tiempo, nada mal. Este porcentaje de mejora es el resultado de las variables trabajando en grupos. - Este efecto aparece si las variables contienen información, como es el caso de
max_heart_rateychest_pain(ovar_1yvar_2). - Colocar variables ruidosas junto a variables buenas usualmente afectará el desempeño global.
- Además el efecto del trabajo en grupos es mayor si las variables de entrada no están correlacionadas entre sí. Es difícil optimizar esto en la práctica. Seguiremos hablando de esto en la siguiente sección…
3.7.4 Rankear las mejores variables usando la Teoría de la Información
Tal como anticipamos al principio de este capítulo, podemos saber la importancia de una variable sin recurrir a un modelo predictivo si utilizamos la Teoría de la Información.
A partir de la versión 1.6.6 el paquete funModeling introduce la función var_rank_info que toma dos argumentos, los datos y la variable objetivo, porque sigue:
variable_importance =
var_rank_info(heart_disease, "has_heart_disease")
# Visualizar resultados
variable_importance## var en mi ig gr
## 1 heart_disease_severity 1.846 0.995 0.9950837595 0.5390655068
## 2 thal 2.032 0.209 0.2094550580 0.1680456709
## 3 exer_angina 1.767 0.139 0.1391389302 0.1526393841
## 4 exter_angina 1.767 0.139 0.1391389302 0.1526393841
## 5 chest_pain 2.527 0.205 0.2050188327 0.1180286190
## 6 num_vessels_flour 2.381 0.182 0.1815217813 0.1157736478
## 7 slope 2.177 0.112 0.1124219069 0.0868799615
## 8 serum_cholestoral 7.481 0.561 0.5605556771 0.0795557228
## 9 gender 1.842 0.057 0.0572537665 0.0632970555
## 10 oldpeak 4.874 0.249 0.2491668741 0.0603576874
## 11 max_heart_rate 6.832 0.334 0.3336174096 0.0540697329
## 12 resting_blood_pressure 5.567 0.143 0.1425548155 0.0302394591
## 13 age 5.928 0.137 0.1371752885 0.0270548944
## 14 resting_electro 2.059 0.024 0.0241482908 0.0221938072
## 15 fasting_blood_sugar 1.601 0.000 0.0004593775 0.0007579095# Graficar
ggplot(variable_importance,
aes(x = reorder(var, gr),
y = gr, fill = var)
) +
geom_bar(stat = "identity") +
coord_flip() +
theme_bw() +
xlab("") +
ylab("Variable Importance
(based on Information Gain)"
) +
guides(fill = FALSE)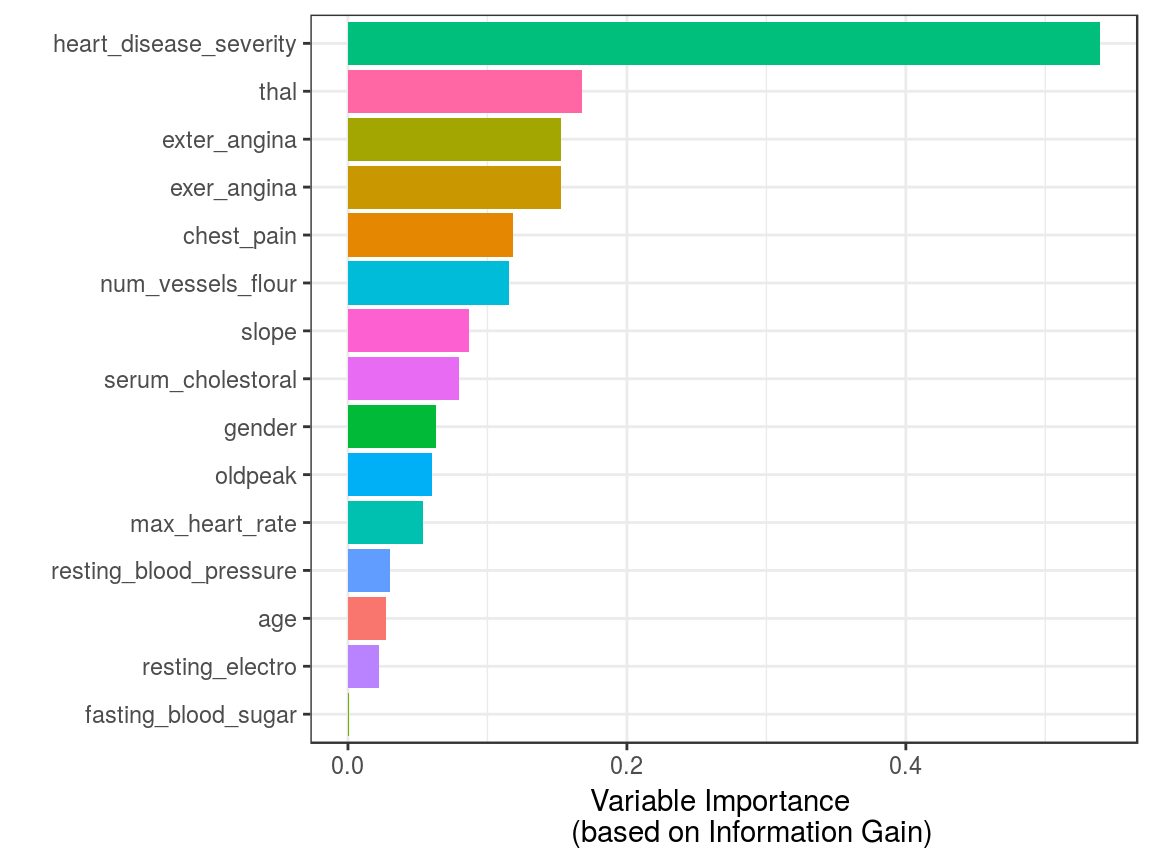
Figure 3.6: Importancia de las variables (basada en la proporción de ganancia)
¿Es heart_disease_severity el factor que explica en mayor medida el objetivo?
No, esta variable fue utilizada para generar el objetivo, por lo que debemos excluirla. Es un error típico cuando desarrollamos un modelo predictivo tener o una variable de entrada que fue construida de la misma manera que el objetivo (como en este caso) o agregar variables del futuro como explicamos en Consideraciones con respecto al tiempo.
Volviendo al resultado de var_rank_info, las métricas resultantes vienen de la Teoría de la información:
en: entropía medida en bitsmi: información mutual (mutual information)ig: ganancia de información (information gain)gr: proporción de ganancia (gain ratio)
En este punto no vamos a detallar qué hay detrás de estas métricas dado que lo cubriremos exclusivamente en un capítulo más adelante. Sin embargo, gain ratio es la métrica más importante aquí, cuyo valor puede ser entre 0 y 1, donde un valor más alto es mejor.
Límites difusos
Acabamos de ver cómo calcular la importancia basándonos en métricas de Teoría de la información. Este tema no es exclusivo de este capítulo; este concepto también aparece en la sección Análisis exploratorio de datos - Correlación y relación.
Seleccionar los mejores factores se relaciona con el análisis exploratorio de datos y viceversa.
3.8 Correlación entre variables de entrada
El escenario ideal es construir un modelo predictivo sólo con variables que no estén correlacionadas entre sí. En la práctica, es complicado mantener este escenario para todas las variables.
Generalmente habrá un conjunto de variables que no están correlacionadas entre sí, pero también habrá otras que tengan al menos alguna correlación.
En la práctica una solución adecuada sería excluir aquellas variables que tengan una correlación notablemente alta.
Sobre cómo medir la correlación. Los resultados pueden ser muy diferentes según se trate de procedimientos lineales o no lineales. Encontrarán más información en la sección de Correlación.
¿Cuál es el problema de agregar variables correlacionadas?
El problema es que estamos agregando complejidad al modelo: normalmente lleva más tiempo, es más difícil de entender, menos explicable, menos preciso, etc. Este es un efecto que repasamos en ¿Los modelos predictivos pueden manejan la alta cardinalidad? Parte 2. La regla general sería: Intenten agregar las N variables principales que están correlacionadas con el resultado pero no entre ellas. Esto nos lleva a la siguiente sección.
3.9 Manténganlo simple

Figure 3.7: Fractales en la naturaleza
La naturaleza opera de la manera más corta posible. -Aristóteles.
El principio de la Navaja de Ockham: Entre distintas hipótesis, deberíamos elegir la que tenga menos supuestos.
Si reinterpretamos esta oración para aplicarla a machine learning, esas hipótesis pueden ser vistas como variables, por lo que tenemos:
Entre distintos modelos predictivos, deberíamos elegir el que tenga menos variables. (Wikipedia 2017c)
Por supuesto, también está el equilibrio entre agregar-quitar variables y la precisión del modelo.
Un modelo predictivo con un alto número de variables tenderá a sobreajustar. Mientras que, por otro lado, un modelo con un bajo número de variables tenderá a subajustar.
El concepto de alto y bajo es altamente subjetivo a los datos que están siendo analizados. En la práctica, podemos tener alguna métrica de precisión, como por ejemplo, el valor de ROC. Es decir, veríamos algo como:
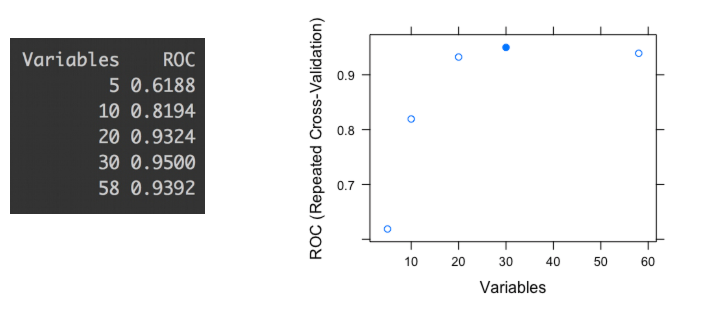
Figure 3.8: Valores de ROC para diferentes subconjuntos de variables
El último gráfico muestra la métrica de precisión ROC de distintos subconjuntos de variables (5, 10, 20, 30 y 58). Cada punto representa el valor ROC dado un determinado número de variables utilizadas para construir el modelo.
Podemos verificar que el valor más alto de ROC aparece cuando el modelo es construido con 30 variables. Si basáramos la selección solamente en un proceso automatizado, podríamos terminar eligiendo un subconjunto que tienda a sobreajustar. Este informe fue producido por la biblioteca caret en R ((Kuhn 2017) pero es análogo para cualquier software.
Observando más de cerca la diferencia entre el subconjunto de 20 y el de 30; hay sólo una mejora de 1.8% -de 0.9324 a 0.95- tomando 10 variables más. En otras palabras: Tomar 50% más variables significará menos de 2% de mejora.
Incluso, este 2% podría ser el margen de error debido a la varianza en la predicción que todo modelo predictivo tiene, como veremos en el capítulo Conociendo el error.
Conclusión:
En este caso, y siendo consecuentes con el principio de la Navaja de Ockham, la mejor solución es construir el modelo con el subconjunto de 20 variables.
Explicar a terceros -y entender- un modelo con 20 variables es más fácil que uno similar pero con 30 variables.
3.10 ¿Selección de variables en agrupamiento (clustering)?
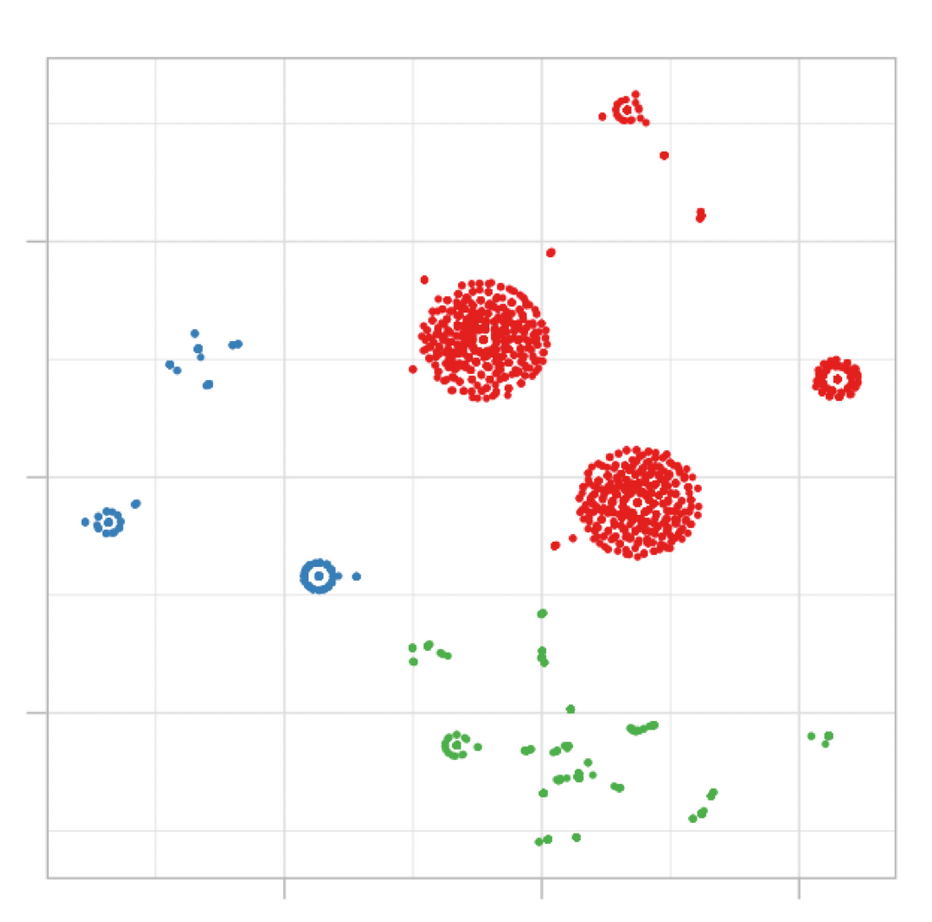
Figure 3.9: Ejemplo de agrupación en segmentos
Este concepto suele aparecer sólo en el modelado predictivo, es decir, tener algunas variables para predecir un objetivo. En la agrupación no hay una variable objetivo, dejamos que los datos hablen, y los grupos naturales surgen de acuerdo a alguna métrica de distancia.
Sin embargo, no todas las variables contribuyen de la misma manera a la diferencia en el modelo de clusters. Siendo breves, si tenemos 3 clusters como resultado, y medimos el promedio de cada variable, esperamos que estos promedios sean bastante diferentes entre sí, ¿cierto?
Habiendo construido 2 modelos de clusters, en el primero los promedios de la variable age son 24, 33 y 26 años; mientras que en el segundo tenemos: 23, 31 y 46. En el segundo modelo la variable age está teniendo más variabilidad, por lo que es más relevante para el modelo.
Este fue sólo un ejemplo considerando dos modelos, pero es lo mismo considerando sólo uno. Aquellas variables con más distancia entre promedios tenderán a definir mejor el cluster que las otras.
A diferencia del modelado predictivo, en el agrupamiento las variables menos importantes no deben ser eliminadas, esas variables no son importantes en ese modelo en particular, pero podrían serlo si construimos otro con otros parámetros. La calidad de los modelos de clusters es muy subjetiva.
Finalmente, podríamos ejecutar, por ejemplo, un modelo de bosque aleatorio con el cluster como variable objetivo y de esta manera identificar rápidamente las variables más importantes.
3.11 Seleccionar las mejores variables en la práctica
3.11.1 La respuesta corta
Tomen las N variables superiores del algoritmo que están usando y luego reconstruyan el modelo con este subconjunto. No todos los modelos predictivos extraen las clasificaciones de las variables, pero si lo hace, utilicen el mismo modelo (por ejemplo, gradient boosting machine) para obtener la clasificación y construir el modelo final.
Para aquellos modelos como k-nearest neighbors, que no tienen incorporado un procedimiento de selección de mejores factores, es válido utilizar la selección de otro algoritmo. Esto conducirá a mejores resultados que el uso de todas las variables.
3.11.2 La respuesta larga
- Cuando sea posible, validen la lista con alguien que conozca el contexto, la industria o el origen de los datos. Ya sea para las N variables superiores o las M variables inferiores. Con respecto a aquellas malas variables, puede que se nos esté escapando algo en el procesamiento de datos que esté destruyendo su poder predictivo.
- Entiendan cada variable, su significado en el contexto (industria, medicina, otros).
- Hagan un análisis exploratorio de datos para ver las distribuciones de las variables más importantes con respecto a la variable objetivo, ¿la selección tiene sentido? Si el objetivo es binario, entonces pueden utilizar la función cross_plot.
- ¿Hay algún promedio de alguna variable que cambie significativamente a lo largo del tiempo? Revisen si hay cambios abruptos en las distribuciones.
- Sospechen de las variables con alta clasificación y alta cardinalidad (como código postal, digamos con más de 100 categorías). Hay más información en Alta cardinalidad en modelado predictivo.
- Cuando estén haciendo la selección -al igual que el modelado predictivo-, traten de usar métodos que tengan algún mecanismo de remuestreo (como bootstrapping), y validación cruzada. Hay más información en el capítulo Conociendo el error.
- Prueben otros métodos para encontrar grupos de variables, como el que mencionamos antes: mRMR.
- Si la selección no se ajusta a las necesidades, prueben creando nuevas variables. Pueden referirse al capítulo de preparación de datos. Muy pronto: un capítulo sobre ingeniería de factores.
3.11.3 Generen su propio conocimiento
Es difícil generalizar cuando la naturaleza de los datos es tan diferente, desde la genética en la que hay miles de variables y unas pocas filas, hasta la navegación web donde llegan nuevos datos todo el tiempo.
Lo mismo aplica al objetivo del análisis. ¿Se utilizará en una competición en la que la precisión es muy necesaria? Tal vez la solución pueda incluir más variables correlacionadas en comparación con un estudio ad-hoc en el que el objetivo principal sea una explicación simple.
No hay una respuesta única para hacer frente a todos los desafíos posibles; ustedes encontrarán poderosas ideas y revelaciones usando su experiencia. Es sólo cuestión de práctica.

3.12 Análisis del objetivo
3.12.1 Usando cross_plot (dataViz)
3.12.1.1 ¿De qué se trata esto?
Este gráfico busca mostrar en escenarios reales si una variable es importante o no, haciendo un resumen visual de la misma, (agrupando variables numéricas en segmentos).
3.12.1.2 Ejemplo 1: ¿El género está correlacionado con las enfermedades cardíacas?
cross_plot(heart_disease, input="gender", target="has_heart_disease")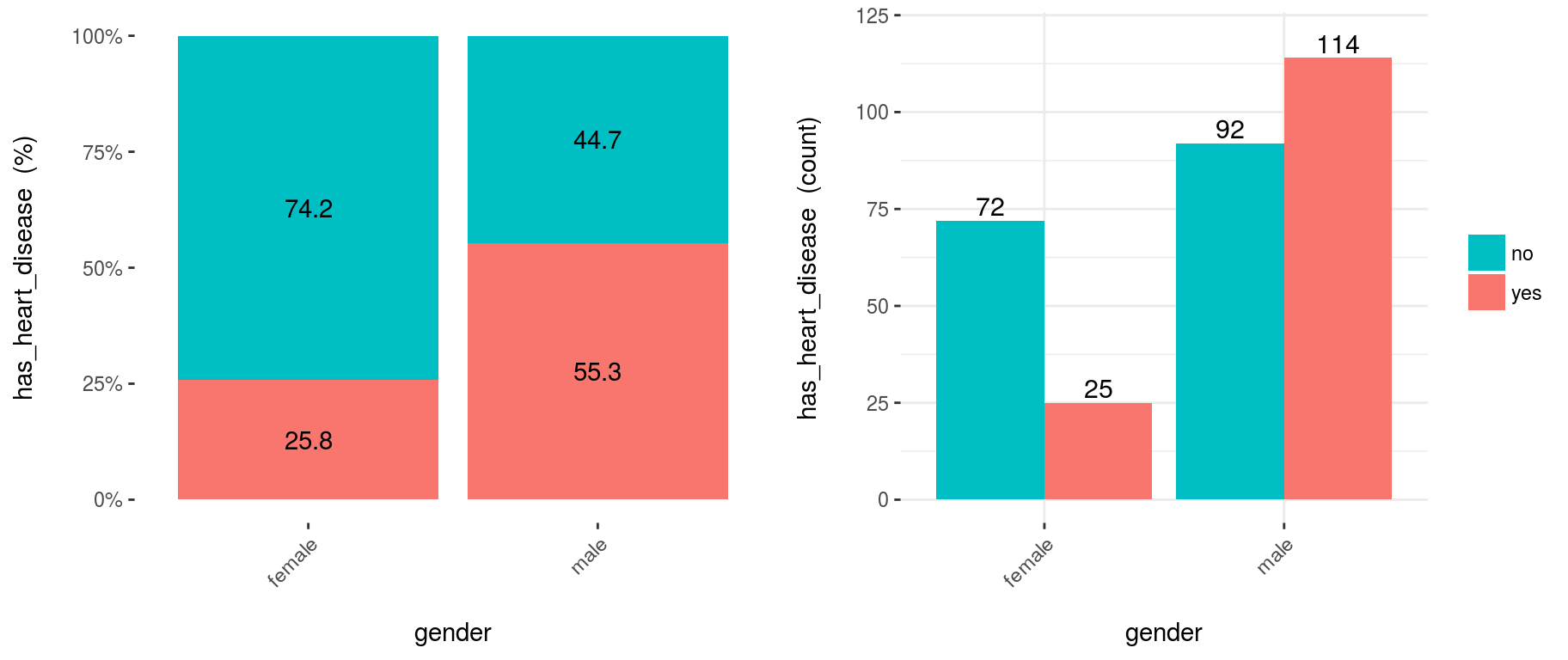
Figure 3.10: Usando cross-plot para analizar y reportar la importancia de las variables
Los últimos dos gráficos comparten la misma fuente de datos, y muestran la distribución de has_heart_disease con respecto a gender. El gráfico de la izquierda la muestra en valor porcentual, mientras el de la derecha la muestra en valor absoluto.
3.12.1.2.1 ¿Cómo extraer conclusiones de los gráficos? (Versión corta)
La variable Gender parece ser un buen predictor, dado que la probabilidad de tener una enfermedad cardíaca es diferente para los grupos mujer/hombre. Le da un orden a los datos.
3.12.1.3 ¿Cómo extraer conclusiones de los gráficos? (Versión larga)
Del 1er gráfico (%):
- La probabilidad de tener una enfermedad cardíaca para los hombres es de 55.3%, mientras para las mujeres es: 25.8%.
- La tasa de enfermedad cardíaca en los hombres es el doble de la tasa en mujeres (55.3 vs. 25.8, respectivamente).
Del 2do gráfico (cantidad):
- Hay un total de 97 mujeres:
- 25 de ellas tienen una enfermedad cardíaca (25/97=25.8%, que es la proporción del 1er gráfico).
- las 72 restantes no tienen una enfermedad cardíaca (74.2%)
- Hay un total de 206 hombres:
- 114 de ellos tienen una enfermedad cardíaca (55.3%)
- los 92 restantes no tienen una enfermedad cardíaca (44.7%)
- Casos totales: Sumar los valores de las cuatro barras: 25+72+114+92=303.
Nota: ¿Qué hubiera pasado si en lugar de tener tasas de 25.8% vs. 55.3% (mujer vs. hombre), hubieran tenido tasas más similares, como 30.2% vs. 30.6%? En ese caso, la variable gender hubiera sido mucho menos relevante, dado que no separa el evento has_heart_disease.
3.12.1.4 Ejemplo 2: Cruzando con variables numéricas
Las variables numéricas deberían estar segmentadas para graficarlas con un histograma, si no, el gráfico no muestra información, como podemos ver aquí:
3.12.1.4.1 Segmentación por igual frecuencia
Hay una función incluida en el paquete (heredada del paquete Hmisc): equal_freq, que devuelve los segmentos basándose en el criterio de igual frecuencia, que tiene -o trata de tener- la misma cantidad de filas por segmento.
Para variables numéricas, cross_plot tiene por defecto auto_binning=T, que automáticamente ejecuta la función equal_freq con n_bins=10 (o el número más cercano).
cross_plot(heart_disease, input="max_heart_rate", target="has_heart_disease")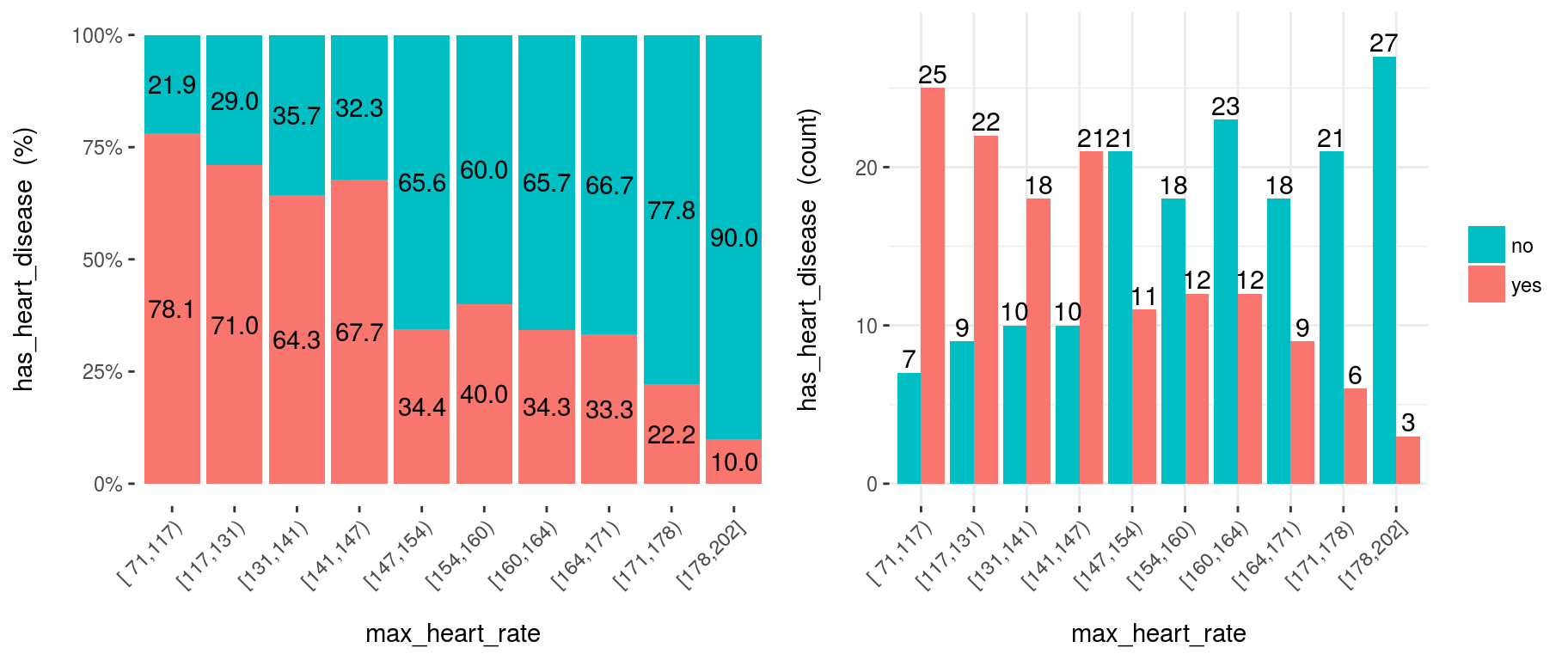
Figure 3.11: Variable numérica como dato de entrada (segmentación automática)
3.12.1.5 Ejemplo 3: Segmentación manual
Si no quieren la segmentación automática, entonces configuren auto_binning=F en la función cross_plot.
Por ejemplo, crear oldpeak_2 basada en igual frecuencia, con tres segmentos.
heart_disease$oldpeak_2 =
equal_freq(var=heart_disease$oldpeak, n_bins = 3)
summary(heart_disease$oldpeak_2)## [0.0,0.2) [0.2,1.5) [1.5,6.2]
## 106 107 90Graficar la variable segmentada (auto_binning = F):
cross_oldpeak_2=cross_plot(heart_disease, input="oldpeak_2", target="has_heart_disease", auto_binning = F)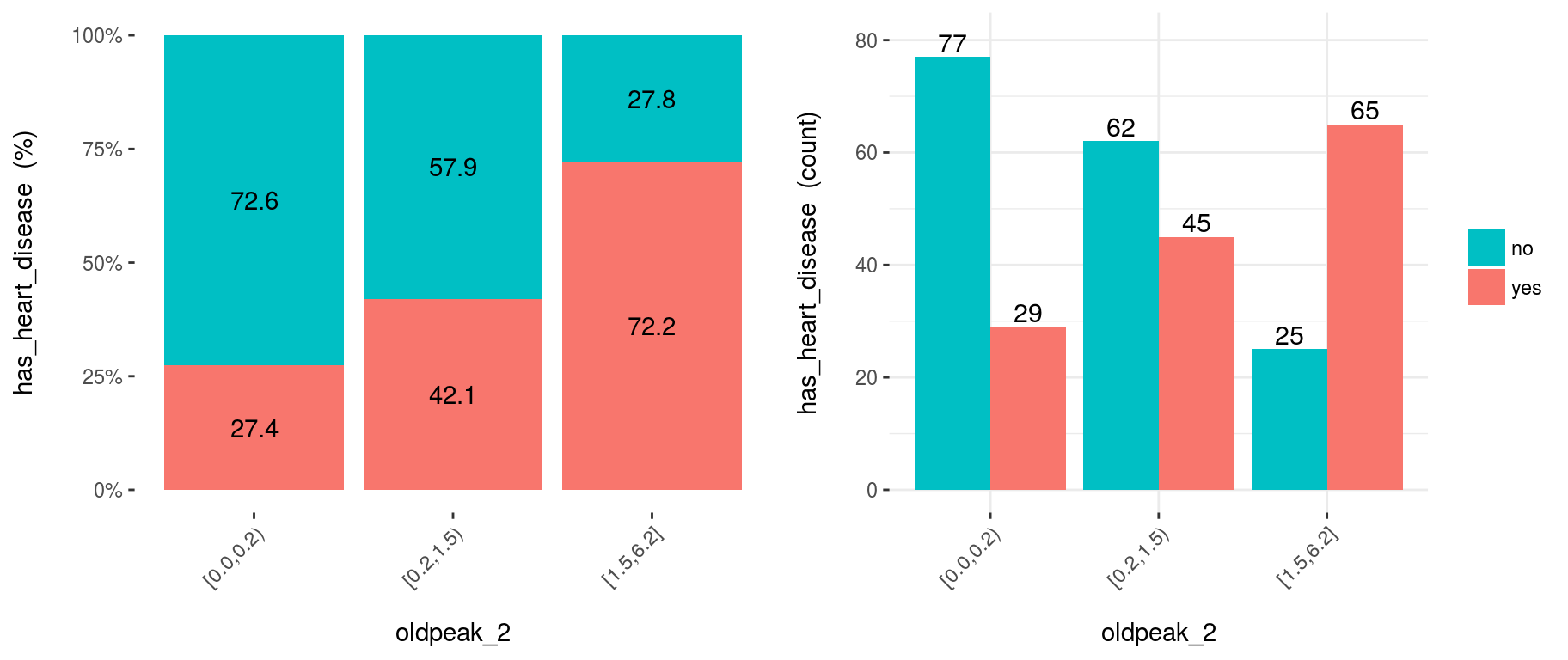
Figure 3.12: Al desactivar la segmentación automática vemos la variable original
3.12.1.5.1 Conclusión
Este nuevo gráfico basado en oldpeak_2 muestra claramente cómo la probabilidad de tener una enfermedad cardíaca aumenta mientras que oldpeak_2 aumenta también. Nuevamente, da un orden a los datos.
3.12.1.6 Ejemplo 4: Reducir el ruido
Convertir la variable max_heart_rate en una de 10 segmentos:
heart_disease$max_heart_rate_2 =
equal_freq(var=heart_disease$max_heart_rate, n_bins = 10)
cross_plot(heart_disease,
input="max_heart_rate_2",
target="has_heart_disease"
)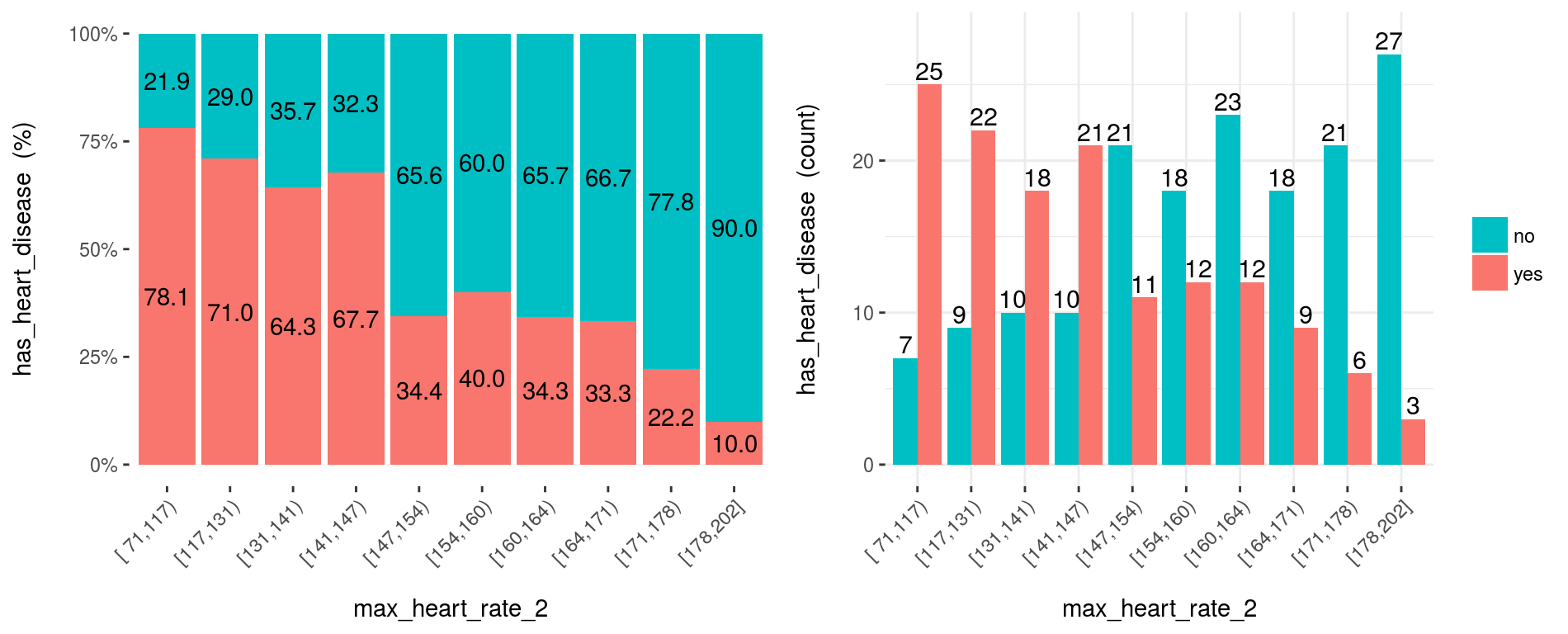
Figure 3.13: Graficar usando segmentación personalizada
A simple vista, max_heart_rate_2 muestra una relación negativa y lineal. Sin embargo, hay algunos segmentos que agregan ruido a la relación. Por ejemplo, el segmento (141, 147] tiene una tasa de enfermedad cardíaca más alta que el segmento anterior, y se esperaba que tuviera una más baja. Esto podría ser ruido en los datos.
Nota clave: Una forma de reducir el ruido (a costa de perder información), es dividir en menos segmentos:
heart_disease$max_heart_rate_3 =
equal_freq(var=heart_disease$max_heart_rate, n_bins = 5)
cross_plot(heart_disease,
input="max_heart_rate_3",
target="has_heart_disease"
)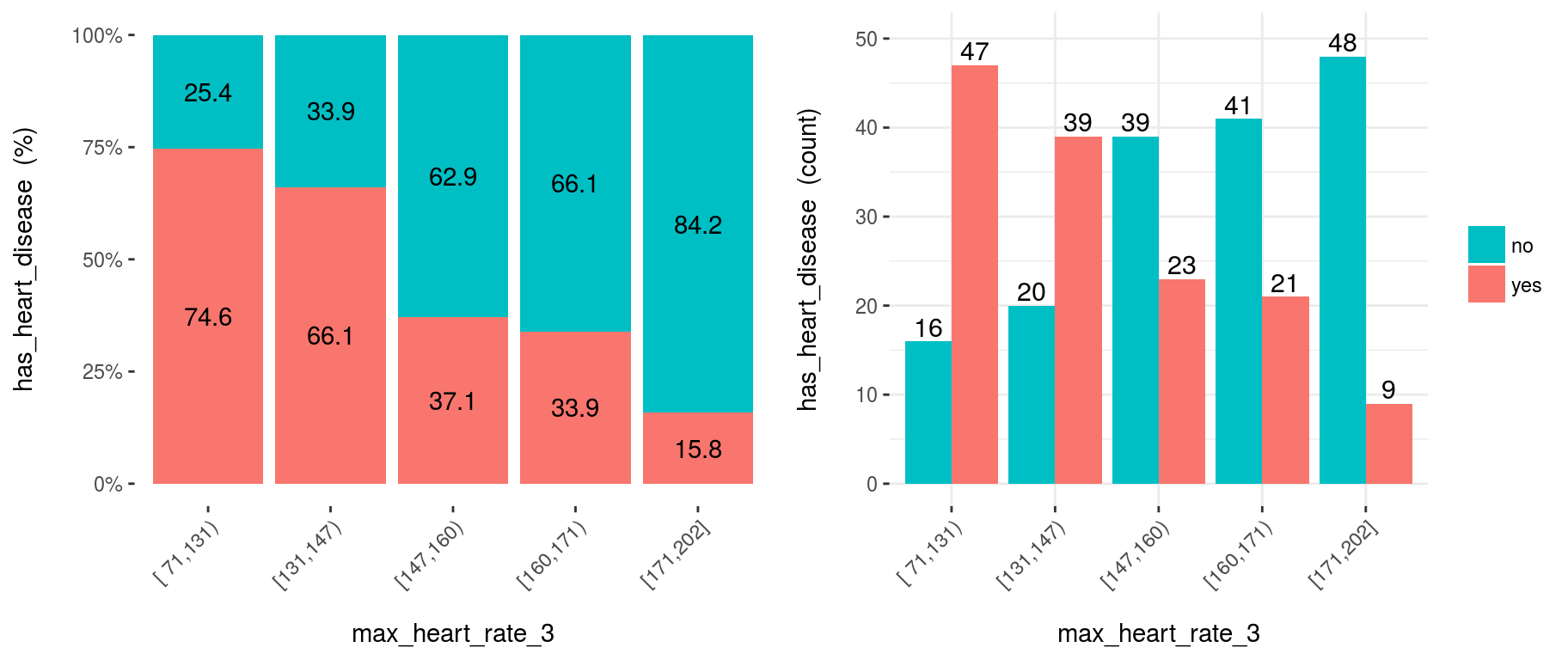
Figure 3.14: Reducir la cantidad de segmentos puede ayudar a exponer mejor la relación
Conclusión: Como podemos ver, ahora la relación es mucho más limpia y clara. El segmento ‘N’ tiene una tasa más alta que ‘N+1’, lo que implica una correlación negativa.
¿Y si guardamos el resultado de cross_plot en una carpeta?
Simplemente creen el parámetro path_out con la carpeta que quieran -Crea una nueva si no existe la que ingresaron-.
cross_plot(heart_disease, input="max_heart_rate_3", target="has_heart_disease", path_out="my_plots")Este comando crea la carpeta my_plots en el directorio en uso.
3.12.1.7 Ejemplo 5: cross_plot en múltiples variables
Imaginen que quieren ejecutar cross_plot en una cantidad de variables al mismo tiempo. Para lograr esto sólo es necesario definir un vector que contenga los nombres de las variables.
Si desean analizar estas 3 variables:
vars_to_analyze=c("age", "oldpeak", "max_heart_rate")cross_plot(data=heart_disease, target="has_heart_disease", input=vars_to_analyze)3.12.1.8 Exportar gráficos
Las funciones plotar y cross_plot pueden manejar de 1 a N variables de entrada, y los gráficos que se generan a partir de ellas pueden exportarse fácilmente en alta calidad con el parámetro path_out.
plotar(data=heart_disease, input=c('max_heart_rate', 'resting_blood_pressure'), target="has_heart_disease", plot_type = "boxplot", path_out = "my_awsome_folder")
3.12.2 Usando boxplots
3.12.2.1 ¿De qué se trata esto?
El uso de boxplots en el análisis de importancia de variables brinda una vistazo rápido de cuán diferentes son los cuartiles entre los distintos valores de una variable objetivo binaria.
# ¡Cargar funModeling!
library(funModeling)
data(heart_disease)plotar(data=heart_disease, input="age", target="has_heart_disease", plot_type = "boxplot")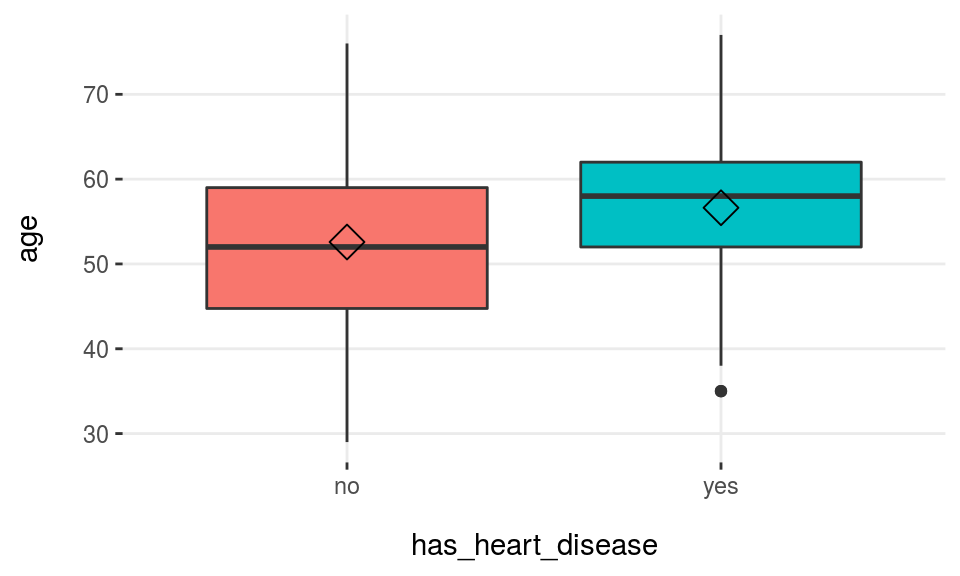
Figure 3.15: Análisis numérico de la variable objetivo usando boxplots
El romboide cerca de la línea de promedio representa la mediana.
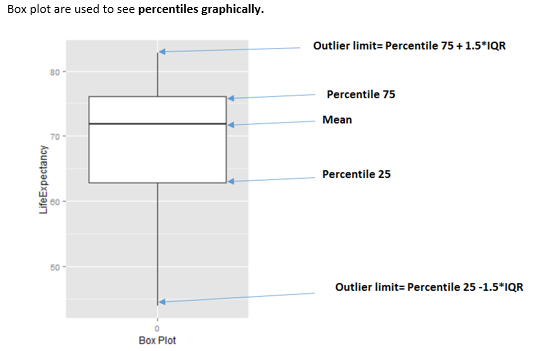
Figure 3.16: Cómo interpretar un diagrama de caja
¿Cuándo usar diagramas de caja?
Cuando necesitamos analizar diferentes percentiles entre las clases para predecir. Noten que esta es una técnica poderosa ya que el sesgo producido debido a los valores atípicos no afecta tanto como afecta al promedio.
3.12.2.2 Boxplot: Variable buena vs. variable mala
Usar más de una variable de entrada es útil para comparar rápidamente los diagramas de caja, y así obtener las mejores variables…
plotar(data=heart_disease, input=c('max_heart_rate', 'resting_blood_pressure'), target="has_heart_disease", plot_type = "boxplot")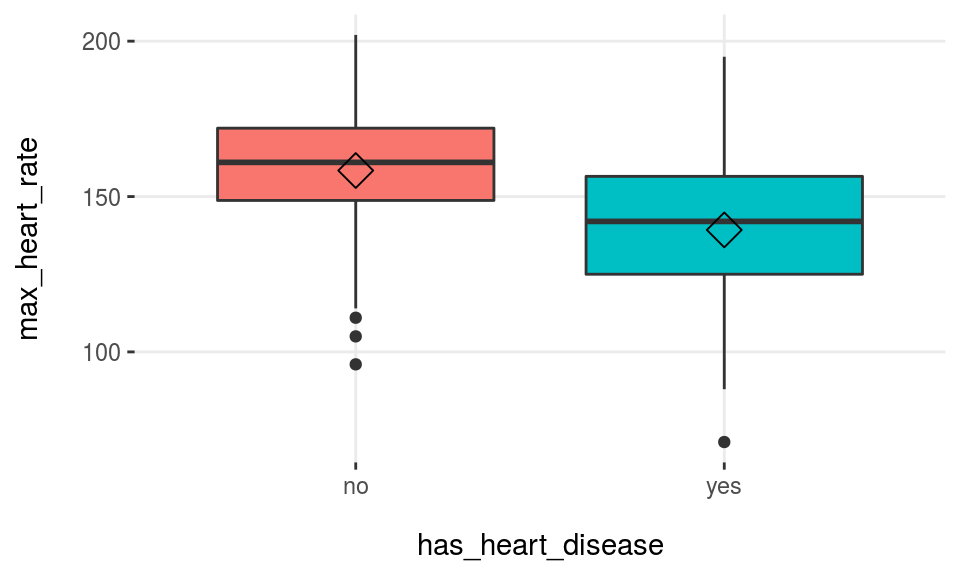
Figure 3.17: Función plotar para variables múltiples
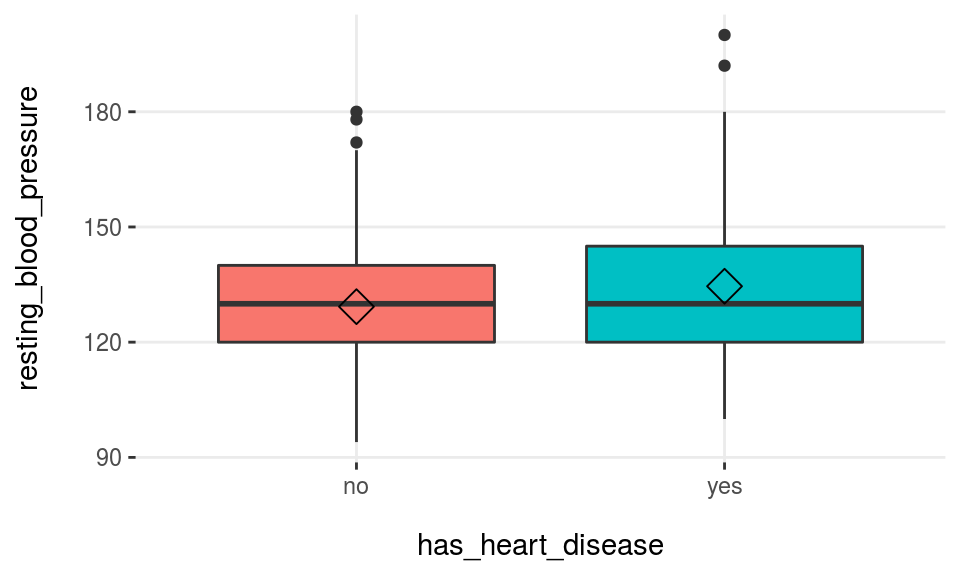
Figure 3.17: Función plotar para variables múltiples
Podemos concluir que max_heart_rate es un mejor predictor que resting_blood_pressure.
Como regla general, una variable se clasificará como más importante si los boxplots no están alineados horizontalmente.
Pruebas estadísticas: los percentiles son otra característica utilizada por ellos para determinar -por ejemplo- si los promedios entre grupos son o no los mismos.
3.12.2.3 Exportando gráficos
plotar y cross_plot pueden manejar desde 1 hasta N variables de entrada, y los gráficos que generan pueden exportarse fácilmente en alta calidad con el parámetro path_out.
plotar(data=heart_disease, input=c('max_heart_rate', 'resting_blood_pressure'), target="has_heart_disease", plot_type = "boxplot", path_out = "my_awsome_folder")- Tengan esto en mente cuando usen diagramas de caja Son agradables a la vista cuando la variable:
- Tiene una buena dispersión -no está concentrada en 3, 4..6.. valores distintos, y
- No tiene valores atípicos extremos… (este punto se puede tratar con la función
prep_outliers, incluida en este paquete)
3.12.3 Usando histogramas de densidad
3.12.3.1 ¿De qué se trata esto?
Los histogramas de densidad son bastante estándar en cualquier libro/recurso cuando se grafican las distribuciones. Usarlas en la selección de variables brinda un vistazo rápido de lo bien que ciertas variables separan la clase.
plotar(data=heart_disease, input="age", target="has_heart_disease", plot_type = "histdens")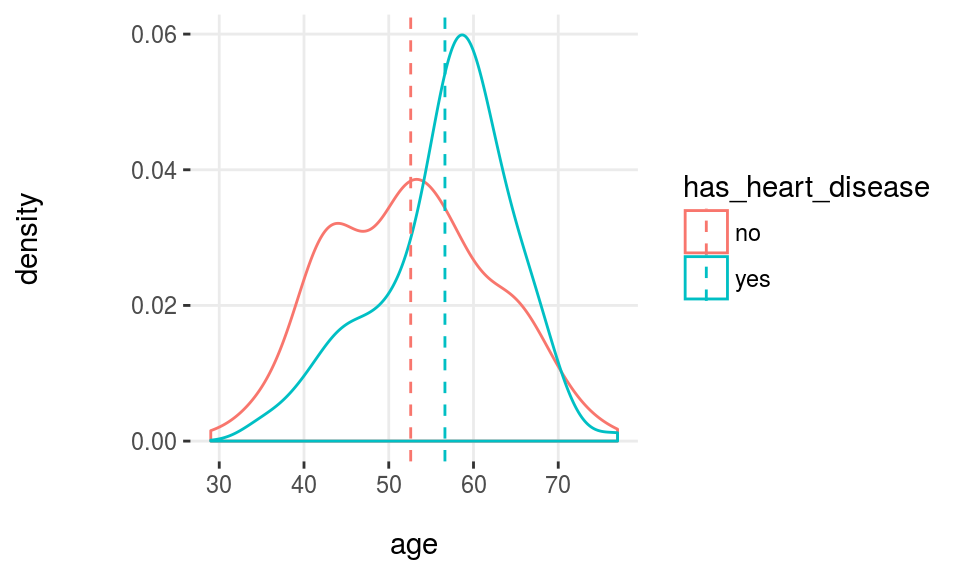
Figure 3.18: Análisis numérico de la variable objetivo usando histogramas de densidad
Nota: La línea punteada representa el promedio de la variable.
Los histogramas de densidad son útiles para visualizar la forma general de una distribución numérica.
Esta forma general se calcula en base a una técnica llamada Kernel smoother (Suavizador Kernel), su idea general es reducir los picos altos/bajos (ruido) presentes en puntos/barras cercanos estimando la función que describe los puntos. Aquí hay algunas imágenes para ilustrar el concepto: https://en.wikipedia.org/wiki/Kernel_smoother
3.12.3.2 ¿Cuál es la relación con una prueba estadística?
Algo similar es lo que ve una prueba estadística: miden cuán diferentes son las curvas que la reflejan en algunas estadísticas como el p-value que se utiliza en el enfoque del frecuentista. Proporciona al analista información confiable para determinar si las curvas tienen -por ejemplo- el mismo promedio.
3.12.3.3 Variable buena vs. variable mala
plotar(data=heart_disease, input=c('resting_blood_pressure', 'max_heart_rate'), target="has_heart_disease", plot_type = "histdens")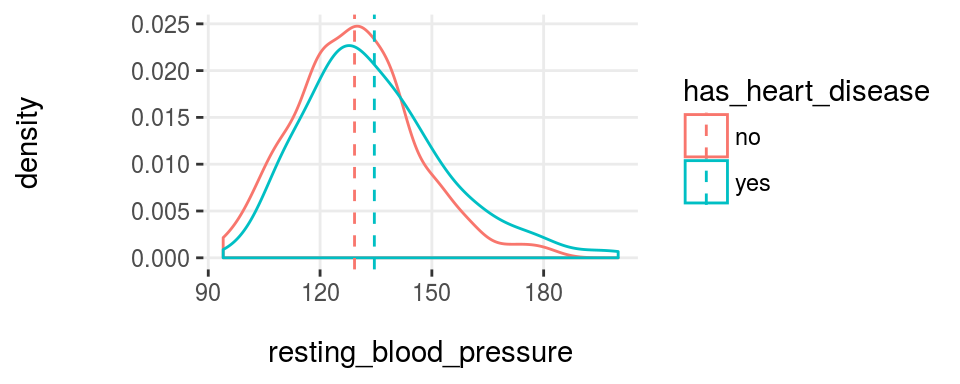
Figure 3.19: Función plotar para variables múltiples
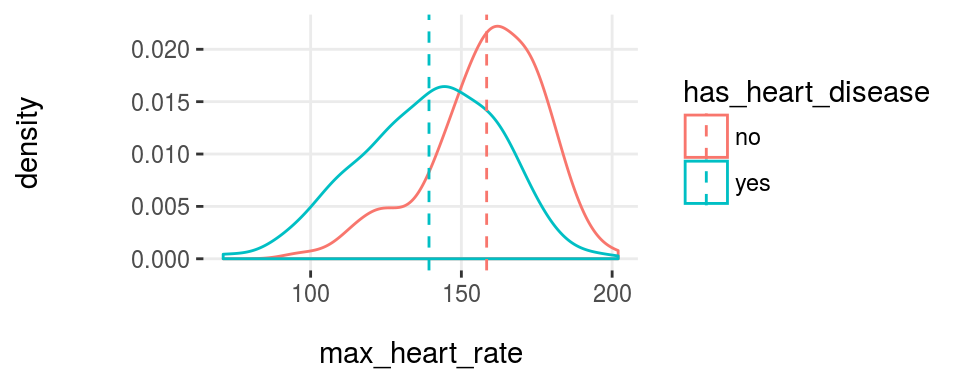
Figure 3.19: Función plotar para variables múltiples
Y el modelo verá lo mismo… si las curvas están bastante superpuestas, como están en resting_blood_pressure, entonces no es un buen predictor, como sí lo sería si estuvieran más espaciadas -como en max_heart_rate.
Tengan esto en mente cuando usen histogramas y diagramas de caja Son agradables a la vista cuando la variable: + Tiene una buena dispersión -no está concentrada en 3, 4..6.. valores distintos, y + No tiene valores atípicos extremos… (este punto se puede tratar con la función prep_outliers, incluida en este paquete)

Referencias
stackoverflow.com. 2017. “What Is Entropy and Information Gain?” http://stackoverflow.com/questions/1859554/what-is-entropy-and-information-gain.
stats.stackexchange.com. 2015. “Gradient Boosting Machine Vs Random Forest.” https://stats.stackexchange.com/questions/173390/gradient-boosting-tree-vs-random-forest.
2017a. “How to Interpret Mean Decrease in Accuracy and Mean Decrease Gini in Random Forest Models.” http://stats.stackexchange.com/questions/197827/how-to-interpret-mean-decrease-in-accuracy-and-mean-decrease-gini-in-random-fore.Wikipedia. 2017c. “Occam’s Razor.” https://en.wikipedia.org/wiki/Occam's_razor#Probability_theory_and_statistics.
Kuhn, Max. 2017. “Recursive Feature Elimination in R Package Caret.” https://topepo.github.io/caret/recursive-feature-elimination.html.