2 Preparación de datos
2.1 Manejando tipos de datos
2.1.1 ¿De qué se trata esto?
Una de las primeras cosas que hay que hacer cuando empezamos un proyecto de datos es asignar el tipo de datos correcto para cada variable. Aunque esto parece una tarea sencilla, algunos algoritmos funcionan con ciertos tipos de datos. Aquí trataremos de cubrir estas conversiones mientras explicamos con ejemplos las implicaciones en cada caso.
Figure 2.1: Espiral de Fibonacci
La sucesión de Fibonacci. Una secuencia de números presente en la naturaleza y en los cuerpos humanos.
¿Qué vamos a repasar en este capítulo?
- Detección del tipo de datos correcto
- Cómo convertir de categórico a numérico
- Cómo convertir de numérico a categórico (métodos de discretización)
- Aspectos teóricos y prácticos (ejemplos en R)
- Cómo observa las variables numéricas un modelo predictivo
2.1.2 El universo de los tipos de datos
Hay dos tipos principales de datos, numérico y categórico. Otros nombres para categóricos son string y nominal.
Un subconjunto de categórico es el ordinal o, como se lo llama en R, un factor ordenado. Al menos en R, este tipo sólo es relevante cuando se grafican categorías en un orden determinado. Un ejemplo en R:
# Crear un factor ordinal u ordenado
var_factor=factor(c("3_high", "2_mid", "1_low"))
var_ordered=factor(var_factor, ordered = T)
var_ordered## [1] 3_high 2_mid 1_low
## Levels: 1_low < 2_mid < 3_highNo presten demasiada atención a este tipo de datos, ya que los numéricos y categóricos son los más necesarios.
2.1.2.1 Variable binaria: ¿numérica o categórica?
Este libro sugiere utilizar las variables binarias como numéricas cuando 0 es FALSE y 1 es TRUE. Simplifica el análisis matemático de los datos.
2.1.3 Tipos de datos por algoritmo
Algunos algoritmos funcionan de la siguiente manera:
- 📊 Sólo con datos categóricos
- 📏 Sólo con datos numéricos
- 📊📏 Con ambos tipos
Además, no todos los modelos predictivos pueden manejar valores faltantes.
El Data Science Live Book busca cubrir todas estas situaciones.
2.1.4 Convirtiendo variables categóricas en numéricas
Usar el paquete caret en R es una tarea sencilla que convierte cada variable categórica en una variable flag, también conocida como variable dummy.
Si la variable categórica original tiene treinta valores posibles, entonces resultará en 30 nuevas columnas que contengan el valor 0 o 1, donde 1 representa la presencia de esa categoría en la fila.
Si usamos el paquete caret de R, entonces para esta conversión sólo se necesitan dos líneas de código:
library(caret) # contiene la función dummyVars
library(dplyr) # librería de data munging
library(funModeling) # df_status function
# Comprobar variables categóricas
status=df_status(heart_disease, print_results = F)
filter(status, type %in% c("factor", "character")) %>% select(variable)## variable
## 1 gender
## 2 chest_pain
## 3 fasting_blood_sugar
## 4 resting_electro
## 5 thal
## 6 exter_angina
## 7 has_heart_disease# Convierte todas las variables categóricas (factor y carácter) en variables numéricas.
# Se salta la variable original, por lo que no es necesario eliminarla después de la conversión, los datos están listos para usar.
dmy = dummyVars(" ~ .", data = heart_disease)
heart_disease_2 = data.frame(predict(dmy, newdata = heart_disease))
# Comprobar el nuevo conjuntos de datos numéricos:
colnames(heart_disease_2)## [1] "age" "gender.female"
## [3] "gender.male" "chest_pain.1"
## [5] "chest_pain.2" "chest_pain.3"
## [7] "chest_pain.4" "resting_blood_pressure"
## [9] "serum_cholestoral" "fasting_blood_sugar.0"
## [11] "fasting_blood_sugar.1" "resting_electro.0"
## [13] "resting_electro.1" "resting_electro.2"
## [15] "max_heart_rate" "exer_angina"
## [17] "oldpeak" "slope"
## [19] "num_vessels_flour" "thal.3"
## [21] "thal.6" "thal.7"
## [23] "heart_disease_severity" "exter_angina.0"
## [25] "exter_angina.1" "has_heart_disease.no"
## [27] "has_heart_disease.yes"Los datos originales heart_disease han sido convertidos a heart_disease_2 que no tiene variables categóricas, sólo numéricas y dummy. Observe que cada nueva variable tiene un punto seguido por el valor.
Si comprobamos el antes y el después para el séptimo paciente (fila) en la variable chest_pain que puede tomar los valores 1, 2, 3 o 4, entonces
# Antes
as.numeric(heart_disease[7, "chest_pain"])## [1] 4# Después
heart_disease_2[7, c("chest_pain.1", "chest_pain.2", "chest_pain.3", "chest_pain.4")]## chest_pain.1 chest_pain.2 chest_pain.3 chest_pain.4
## 7 0 0 0 1Habiendo conservado y transformado sólo variables numéricas excluyendo las nominales, los datos heart_disease_2 están listos para ser utilizados.
Hay más información sobre dummyVars en: http://amunategui.github.io/dummyVar-Walkthrough/
2.1.5 ¿Es categórica o numérica? Piénsenlo.
Consideren la variable chest_pain, que puede tomar los valores 1, 2, 3, o 4. ¿Es esta variable categórica o numérica?
Si los valores están ordenados, entonces se la puede considerar tan numérica como si exhibiera un orden, es decir, 1 es menos de 2, 2 es menos de 3, y 3 es menos de 4.
Si creamos un modelo de árbol de decisión, entonces podemos encontrar reglas como: “Si el dolor de pecho es > 2.5, entonces…”. ¿Tiene sentido? El algoritmo divide la variable por un valor que no está presente (2.5); sin embargo, la interpretación que hacemos es “si dolor de pecho es igual o superior a 3, entonces…”.
2.1.6 Pensar como un algoritmo
Considere dos variables numéricas de entrada y una variable binaria de destino. El algoritmo verá ambas variables de entrada como puntos en un rectángulo, considerando que hay valores infinitos entre cada número.
Por ejemplo, una Máquina de Soporte Vectorial (SVM) creará varios vectores para separar la clase de la variable de destino. Encontrará regiones basadas en estos vectores. ¿Cómo sería posible encontrar estas regiones basándose en variables categóricas? No es posible y es por eso que el SVM sólo funciona con variables numéricas como en las redes neuronales artificiales.
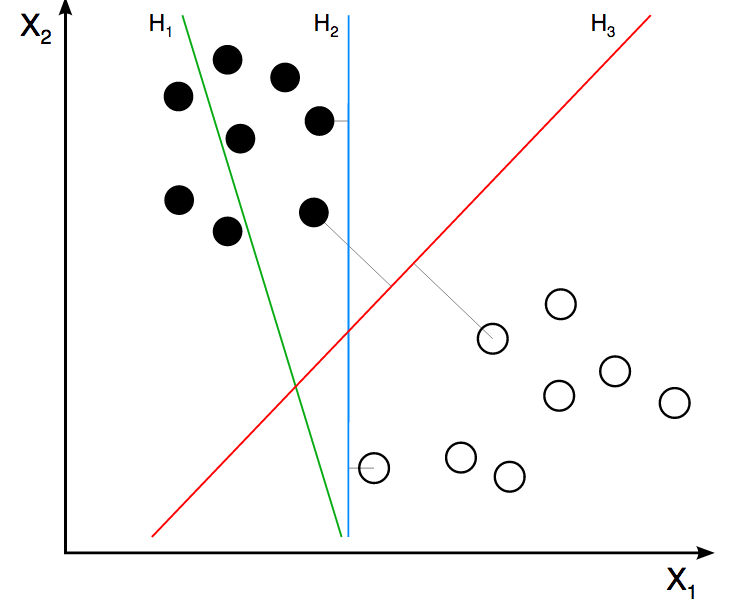
Figure 2.2: Máquina de vectores soporte
Image credit: ZackWeinberg
La última imagen muestra tres líneas, que representan tres límites de decisión o regiones diferentes.
Para una rápida introducción a este concepto de SVM, por favor vean este corto video: Demo SVM.
Sin embargo, si el modelo está basado en árboles, como decision trees, random forest o gradient boosting machine, entonces manejan ambos tipos porque su espacio de búsqueda puede ser regiones (igual que SVM) y categorías. Como la regla “si postal_code es AX441AG y tiene más de 55 años, entonces...”.
Volviendo al ejemplo de la enfermedad cardíaca, la variable chest_pain exhibe orden. Debemos aprovechar esto porque si lo convertimos en una variable categórica, entonces estamos perdiendo información y este es un punto importante a la hora de manejar los tipos de datos.
2.1.6.1 ¿Es la solución tratar a todas las variables como categóricas?
No…. Una variable numérica contiene más información que una nominal debido a su orden. En las variables categóricas, los valores no se pueden comparar. Digamos que no es posible hacer una regla como Si el código postal es superior a "AX2004-P".
Los valores de una variable nominal pueden ser comparados si tenemos otra variable para usar como referencia (normalmente un resultado a predecir).
Por ejemplo, el código postal “AX2004-P” es más alto que “MA3942-H” porque hay más personas interesadas en asistir a clases de fotografía.
Además, la alta cardinalidad es un problema en las variables categóricas, por ejemplo, una variable postal code que contiene cientos de valores diferentes. Este libro ha tratado este tema en ambos capítulos: el manejo de variables de alta categorización para estadísticas descriptivas y cuando hacemos modelado predictivo.
De todos modos, pueden hacer la prueba gratis de convertir todas las variables en categóricas y ver qué pasa. Comparen los resultados con las variables numéricas. Recuerden usar alguna buena medida de error para la prueba, como el estadístico Kappa o ROC, y validar los resultados.
2.1.6.2 Tengan cuidado al convertir variables categóricas en numéricas
Imaginemos que tenemos una variable categórica que necesitamos convertir a numérica. Como en el caso anterior, pero intentando una diferente transformación, asignen un número diferente a cada categoría.
Tenemos que tener cuidado al hacer tales transformaciones porque estamos introduciendo orden a la variable.
Considere el siguiente ejemplo de datos con cuatro filas. Las dos primeras variables son visits y postal_code (esto funciona como dos variables de entrada o visits como entrada y postal_code como salida).
El siguiente código mostrará las visits dependiendo de postal_code transformadas según dos criterios:
transformation_1: Asigna un número de secuencia basado en el orden dado.transformation_2: Asigna un número basado en la cantidad devisits.
# Crear una muestra de datos de juguete
df_pc=data.frame(visits=c(10, 59, 27, 33), postal_code=c("AA1", "BA5", "CG3", "HJ1"), transformation_1=c(1,2,3,4), transformation_2=c(1, 4, 2, 3 ))
# Visualizar la tabla
knitr::kable(df_pc)| visits | postal_code | transformation_1 | transformation_2 |
|---|---|---|---|
| 10 | AA1 | 1 | 1 |
| 59 | BA5 | 2 | 4 |
| 27 | CG3 | 3 | 2 |
| 33 | HJ1 | 4 | 3 |
library(gridExtra)
# Transformación 1
plot_1=ggplot(df_pc, aes(x=transformation_1, y=visits, label=postal_code)) + geom_point(aes(color=postal_code), size=4)+ geom_smooth(method=loess, group=1, se=FALSE, color="lightblue", linetype="dashed") + theme_minimal() + theme(legend.position="none") + geom_label(aes(fill = factor(postal_code)), colour = "white", fontface = "bold")
# Transformación 2
plot_2=ggplot(df_pc, aes(x=transformation_2, y=visits, label=postal_code)) + geom_point(aes(color=postal_code), size=4)+ geom_smooth(method=lm, group=1, se=FALSE, color="lightblue", linetype="dashed") + theme_minimal() + theme(legend.position="none") + geom_label(aes(fill = factor(postal_code)), colour = "white", fontface = "bold")
# Disponer los gráficos uno al lado del otro
grid.arrange(plot_1, plot_2, ncol=2)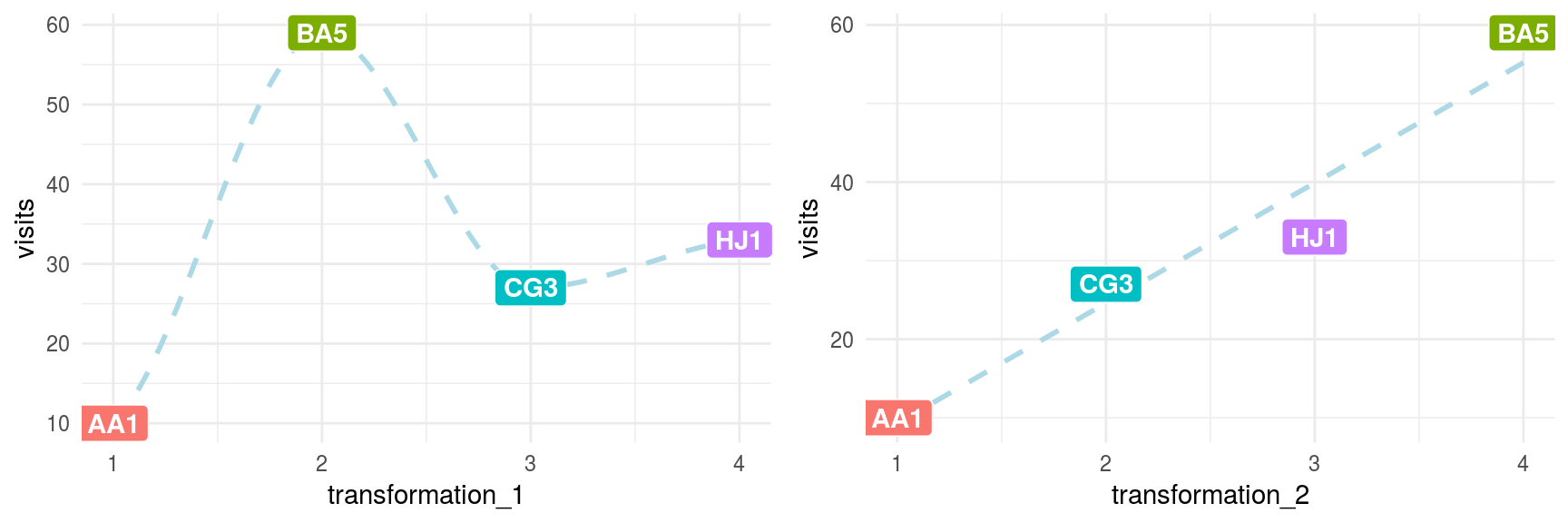
Figure 2.3: Comparación entre transformaciones de datos
Para estar seguros, nadie construye un modelo predictivo usando sólo cuatro filas; sin embargo, la intención de este ejemplo es mostrar cómo la relación cambia de no lineal (transformation_1) a lineal (transformation_2). Esto hace las cosas más fáciles para el modelo predictivo y explica la relación.
El efecto es el mismo cuando manejamos millones de filas de datos y el número de variables escala a cientos. Aprender de datos pequeños es un enfoque adecuado en estos casos.
2.1.7 Discretizando variables numéricas
Este proceso convierte los datos en una categoría dividiéndolos en segmentos. Para una definición más sofisticada, podemos citar a Wikipedia: La discretización refiere al proceso de transferir funciones, modelos y ecuaciones continuas a contrapartes discretas.
Los segmentos también se conocen como bins o buckets. Continuemos con los ejemplos.
2.1.7.1 Sobre los datos
Los datos contienen información sobre el porcentaje de niños con retraso en el crecimiento. El valor ideal es cero.
El indicador refleja la proporción de niños menores de 5 años que presentan retraso en el crecimiento. Los niños con retraso en el crecimiento tienen mayor riesgo de enfermedad y muerte.
Fuente: ourworldindata.org, hunger and undernourishment.
En primer lugar, tenemos que hacer una rápida preparación de datos. Cada fila representa un par país-año, por lo que tenemos que obtener el indicador más reciente por país.
data_stunting=read.csv(file = "https://goo.gl/hFEUfN",
header = T,
stringsAsFactors = F)
# Renombrar la métrica
data_stunting=
dplyr::rename(
data_stunting,
share_stunted_child=
Share.of.stunted.children.under.5
)
# Realizar la agrupación previamente mencionada
d_stunt_grp = group_by(data_stunting, Entity) %>%
filter(Year == max(Year)) %>%
dplyr::summarise(share_stunted_child=
max(share_stunted_child)
)Los criterios de segmentación más comunes son:
- Igual rango
- Igual frecuencia
- Segmentos personalizados
Todos están explicados a continuación.
2.1.7.2 Igual rango
El rango se suele encuentrar en los histogramas que estudian la distribución, pero es altamente susceptible a los valores atípicos. Para crear, por ejemplo, cuatro segmentos, dividimos por 4 los valores mínimos y máximos.
# funModeling contiene equal_freq (discretización)
library(funModeling)
# ggplot2 brinda la función 'cut_interval' que se
# utiliza para dividir las variables en base al
# criterio de igual rango
library(ggplot2)
# Al crear una variable de igual rango, agreguen
# el parámetro `dig.lab=9`para desactivar la
# notación científica al igual que con la
# función `cut`.
d_stunt_grp$share_stunted_child_eq_range=
cut_interval(d_stunt_grp$share_stunted_child, n = 4)
# La función `describe` del paquete Hmisc package es
# extremadamente útil para analizar datos
describe(d_stunt_grp$share_stunted_child_eq_range)## d_stunt_grp$share_stunted_child_eq_range
## n missing distinct
## 154 0 4
##
## Value [1.3,15.8] (15.8,30.3] (30.3,44.8] (44.8,59.3]
## Frequency 62 45 37 10
## Proportion 0.403 0.292 0.240 0.065# Graficar la variable
p2=ggplot(d_stunt_grp,
aes(share_stunted_child_eq_range)
) +
geom_bar(fill="#009E73") +
theme_bw()
p2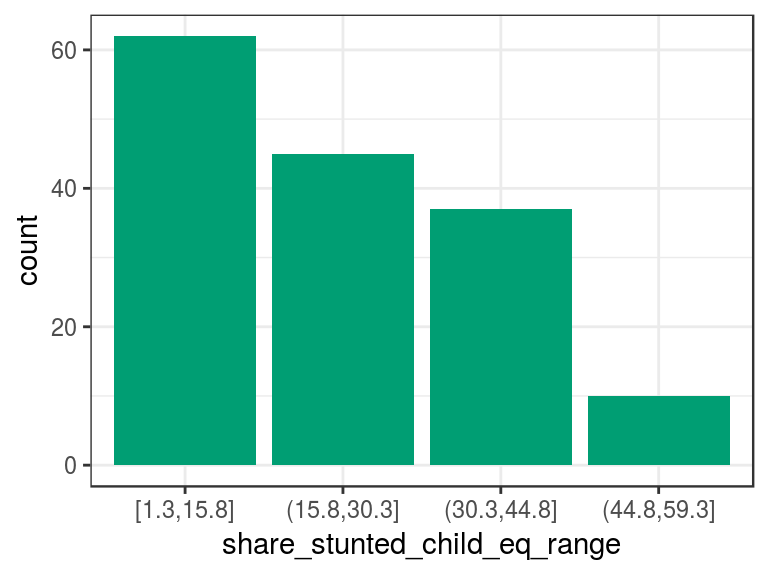
Figure 2.4: Discretización por igual frecuencia
El resultado de describe nos dice que hay cuatro categorías en la variable y, entre paréntesis y corchetes, el número total de casos por categoría tanto en valores absolutos como relativos, respectivamente. Por ejemplo, la categoría (15.8,30.3] contiene todos los casos que tienen share_stunted_child desde 15.8 (no inclusive) hasta 30.3 (inclusive). Aparece 45 veces y representa 29% del total de casos.
2.1.7.3 Igual frecuencia
Esta técnica agrupa la misma cantidad de observaciones utilizando criterios basados en percentiles. Pueden encontrar más información sobre percentiles en el capítulo: Anexo 1: La magia de los percentiles.
El paquete funModeling incluye la función equal_freq para crear segmentos basándonos en este criterio:
d_stunt_grp$stunt_child_ef=
equal_freq(var = d_stunt_grp$share_stunted_child,
n_bins = 4
)
# Analizar la variable
describe(d_stunt_grp$stunt_child_ef)## d_stunt_grp$stunt_child_ef
## n missing distinct
## 154 0 4
##
## Value [ 1.3, 9.5) [ 9.5,20.8) [20.8,32.9) [32.9,59.3]
## Frequency 40 37 39 38
## Proportion 0.260 0.240 0.253 0.247p3=ggplot(d_stunt_grp, aes(stunt_child_ef)) +
geom_bar(fill="#CC79A7") + theme_bw()
p3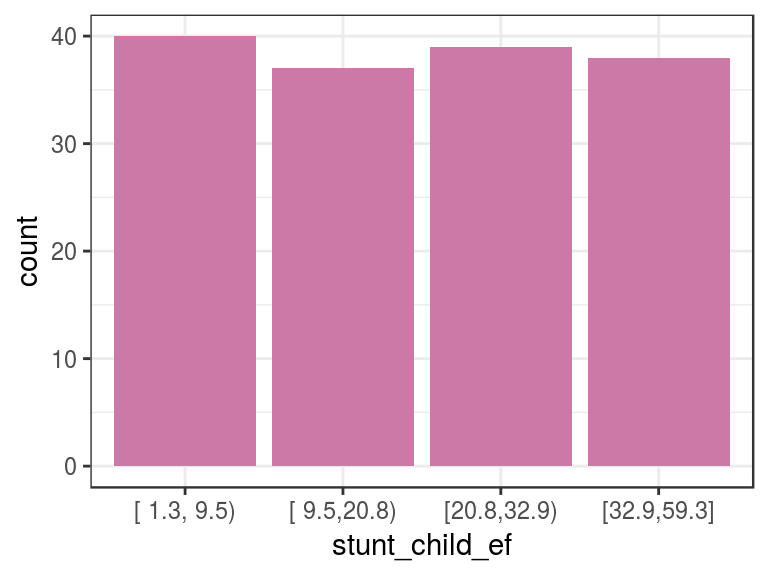
Figure 2.5: Ejemplo de igual frecuencia
En este caso, seleccionamos cuatro segmentos, por lo que cada uno contendrá aproximadamente un 25% del total.
2.1.7.4 Segmentos personalizados
Si ya tenemos los puntos de los cuales queremos los segmentos, podemos usar la función cut.
# El parámetro dig.lab desactiva la notación científica
d_stunt_grp$share_stunted_child_custom=
cut(d_stunt_grp$share_stunted_child,
breaks = c(0, 2, 9.4, 29, 100)
)
describe(d_stunt_grp$share_stunted_child_custom)## d_stunt_grp$share_stunted_child_custom
## n missing distinct
## 154 0 4
##
## Value (0,2] (2,9.4] (9.4,29] (29,100]
## Frequency 5 35 65 49
## Proportion 0.032 0.227 0.422 0.318p4=ggplot(d_stunt_grp, aes(share_stunted_child_custom)) +
geom_bar(fill="#0072B2") +
theme_bw()
p4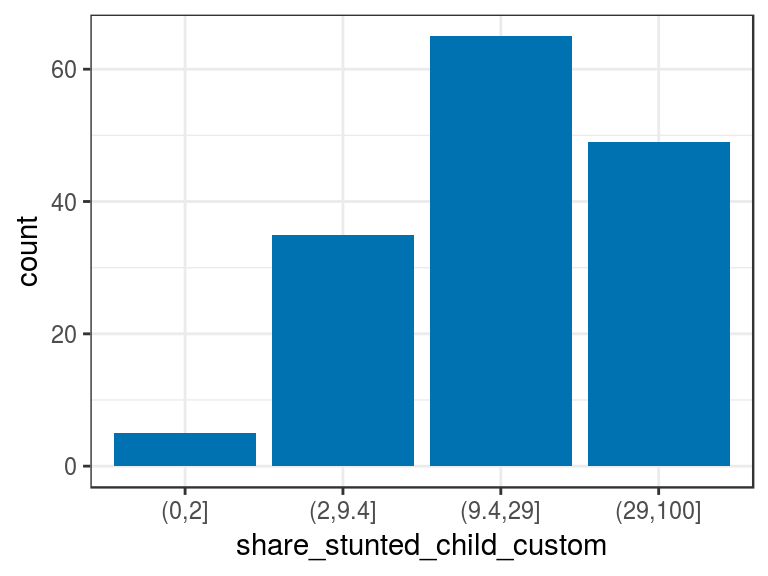
Figure 2.6: Discretización manual
Noten que solo es necesario definir el valor máximo de cada segmento.
Por lo general, no sabemos cuál es el valor mínimo o máximo. En esos casos, podemos utilizar los valores -Inf e Inf. De lo contrario, si definimos un valor que está fuera del rango, cut le asignará el valor NA.
Es una buena práctica asignar el valor mínimo y máximo usando una función. En este caso, la variable es un porcentaje, por lo que sabemos de antemano que su escala es de 0 a 100; sin embargo, ⚠️ ¿qué pasaría si no conociéramos el rango?
La función devolverá NA para aquellos valores por debajo o por encima de los puntos de corte. Una solución es obtener valores mínimos y máximos variables:
# Obtener el valor mínimo y máximo
min_value=min(d_stunt_grp$share_stunted_child)
max_value=max(d_stunt_grp$share_stunted_child)
# Configuren `include.lowest=T` para incluir el valor
# mínimo, de lo contrario será asignado como NA.
d_stunt_grp$share_stunted_child_custom_2=
cut(d_stunt_grp$share_stunted_child,
breaks = c(min_value, 2, 9.4, 29, max_value),
include.lowest = T)
describe(d_stunt_grp$share_stunted_child_custom_2)## d_stunt_grp$share_stunted_child_custom_2
## n missing distinct
## 154 0 4
##
## Value [1.3,2] (2,9.4] (9.4,29] (29,59.3]
## Frequency 5 35 65 49
## Proportion 0.032 0.227 0.422 0.3182.1.8 Discretizacación con nuevos datos
Todas estas transformaciones se realizan con un conjunto de datos de práctica basado en las distribuciones de las variables. Tal es el caso de la discretización de igual frecuencia y de igual rango. Pero, ¿qué pasaría si llegaran nuevos datos?
Si aparece un nuevo valor mínimo o máximo, afectará el rango de ubicaciones en el método igual rango. Si llega algún nuevo valor, entonces moverá los puntos basados en percentiles como vimos en el método igual frecuencia.
Para ver qué pasa, imaginemos que añadimos cuatro casos más en el ejemplo propuesto, con los valores 88, 2, 7 y 3:
# Simular que se agregan cuatro valores nuevos
updated_data=c(d_stunt_grp$share_stunted_child, 88, 2, 7, 3)
# Discretizar por igual frecuencia
updated_data_eq_freq=equal_freq(updated_data,4)
# Resultados en...
describe(updated_data_eq_freq)## updated_data_eq_freq
## n missing distinct
## 158 0 4
##
## Value [ 1.3, 9.3) [ 9.3,20.6) [20.6,32.9) [32.9,88.0]
## Frequency 40 39 40 39
## Proportion 0.253 0.247 0.253 0.247Ahora comparemos con los segmentos que creamos anteriormente:
describe(d_stunt_grp$stunt_child_ef)## d_stunt_grp$stunt_child_ef
## n missing distinct
## 154 0 4
##
## Value [ 1.3, 9.5) [ 9.5,20.8) [20.8,32.9) [32.9,59.3]
## Frequency 40 37 39 38
## Proportion 0.260 0.240 0.253 0.247¡Todos los segmentos cambiaron! 😱 Dado que estas son nuevas categorías, el modelo predictivo fallará a la hora de procesarlas porque son todos valores nuevos.
La solución es conservar los puntos de corte cuando preparamos los datos. Luego, ejecutamos el modelo en producción, utilizamos el segmento de discretización manual y, así, forzamos que cada caso quede en la categoría correspondiente. De esta manera, el modelo predictivo siempre ve lo mismo.
La solución será detallada en la siguiente sección.
2.1.9 Discretización automática de data frames
El paquete funModeling (desde la versión > 1.6.6) introduce dos funciones: discretize_get_bins y discretize_df que operan juntas para ayudarnos en la tarea de discretización.
# Primero cargamos las bibliotecas
# install.packages("funModeling")
library(funModeling)
library(dplyr)Veamos un ejemplo. Primero, corroboramos los tipos de datos actuales:
df_status(heart_disease, print_results = F) %>% select(variable, type, unique, q_na) %>% arrange(type)## variable type unique q_na
## 1 gender factor 2 0
## 2 chest_pain factor 4 0
## 3 fasting_blood_sugar factor 2 0
## 4 resting_electro factor 3 0
## 5 thal factor 3 2
## 6 exter_angina factor 2 0
## 7 has_heart_disease factor 2 0
## 8 age integer 41 0
## 9 resting_blood_pressure integer 50 0
## 10 serum_cholestoral integer 152 0
## 11 max_heart_rate integer 91 0
## 12 exer_angina integer 2 0
## 13 slope integer 3 0
## 14 num_vessels_flour integer 4 4
## 15 heart_disease_severity integer 5 0
## 16 oldpeak numeric 40 0Tenemos variables factor, enteras, y numéricas: ¡una buena mezcla! La transformación tiene dos pasos. Primero, obtiene los valores de corte o de umbral donde comienza cada segmento. El segundo paso es utilizar el umbral para obtener las variables como categóricas.
Discretizaremos dos variables en el siguiente ejemplo: max_heart_rate y oldpeak. Además, agregaremos algunos valores NA a oldpeak para evaluar cómo opera la función con datos faltantes.
# Crear una copia para conservar los datos originales intactos
heart_disease_2=heart_disease
# Introducir algunos valores faltantes en las primeras 30 filas de la variable oldpeak
heart_disease_2$oldpeak[1:30]=NAPaso 1) Obtener los umbrales de segmento para cada variable de entrada:
discretize_get_bins devuelve un data frame que necesitaremos para la función discretize_df, que genera el data frame final procesado.
d_bins=discretize_get_bins(data=heart_disease_2, input=c("max_heart_rate", "oldpeak"), n_bins=5)## [1] "Variables processed: max_heart_rate, oldpeak"# Verificar el objeto `d_bins`:
d_bins## variable cuts
## 1 max_heart_rate 131|147|160|171|Inf
## 2 oldpeak 0.1|0.3|1.1|2|InfParámetros:
data: el data frame que contiene las variables a procesar.input: vector de strings que contienen los nombres de las variables.n_bins: la cantidad de segmentos que tendremos en los datos discretizados.
Podemos ver el punto del umbral (o límite superior) para cada variable.
Nota: Cambios de la versión 1.6.6 a 1.6.7:
discretize_get_binsno crea el umbral-Infdado que dicho valor siempre fue considerado el mínimo.- La categoría de un valor ahora se representa como un rango, por ejemplo, lo que era
"5", ahora es"[5, 6)". - El formato de los segmentos puede haber cambiado, si utilizaron esta función en producción, tienen que verificar los nuevos valores.
¡Es hora de continuar con el siguiente paso!
Paso 2) Aplicar los umbrales para cada variable:
# Ahora se puede aplicar en el mismo data frame o
# en una nueva (por ejemplo, en un modelo predictivo
# en el que los datos cambian con el tiempo)
heart_disease_discretized =
discretize_df(data=heart_disease_2,
data_bins=d_bins,
stringsAsFactors=T)## [1] "Variables processed: max_heart_rate, oldpeak"Parámetros:
data: data frame que contiene las variables a procesar.data_bins: data frame resultado demdiscretize_get_bins. Si el usuario la modifica, entonces cada límite superior deberá estar separado por un carácter pipe (|) como se ve en el ejemplo.stringsAsFactors:TRUEpor defecto, las variables finales serán factor (en lugar de un carácter) y útiles para graficar.
2.1.9.1 Resultados finales y sus gráficos
Antes y después:
## max_heart_rate_before max_heart_rate_after oldpeak_before oldpeak_after
## 1 171 [ 171, Inf] NA NA.
## 2 114 [-Inf, 131) NA NA.
## 3 151 [ 147, 160) 1.8 [ 1.1, 2.0)
## 4 160 [ 160, 171) 1.4 [ 1.1, 2.0)
## 5 158 [ 147, 160) 0.0 [-Inf, 0.1)
## 6 161 [ 160, 171) 0.5 [ 0.3, 1.1)Distribución final:
freq(heart_disease_discretized %>%
select(max_heart_rate,oldpeak),
plot = F)## max_heart_rate frequency percentage cumulative_perc
## 1 [-Inf, 131) 63 20.79 20.79
## 2 [ 147, 160) 62 20.46 41.25
## 3 [ 160, 171) 62 20.46 61.71
## 4 [ 131, 147) 59 19.47 81.18
## 5 [ 171, Inf] 57 18.81 100.00
##
## oldpeak frequency percentage cumulative_perc
## 1 [-Inf, 0.1) 97 32.01 32.01
## 2 [ 0.3, 1.1) 54 17.82 49.83
## 3 [ 1.1, 2.0) 54 17.82 67.65
## 4 [ 2.0, Inf] 50 16.50 84.15
## 5 NA. 30 9.90 94.05
## 6 [ 0.1, 0.3) 18 5.94 100.00## [1] "Variables processed: max_heart_rate, oldpeak"p5=ggplot(heart_disease_discretized,
aes(max_heart_rate)) +
geom_bar(fill="#0072B2") +
theme_bw() +
theme(axis.text.x =
element_text(angle = 45, vjust = 1, hjust=1)
)
p6=ggplot(heart_disease_discretized,
aes(oldpeak)) +
geom_bar(fill="#CC79A7") +
theme_bw() +
theme(axis.text.x =
element_text(angle = 45, vjust = 1, hjust=1)
)
gridExtra::grid.arrange(p5, p6, ncol=2)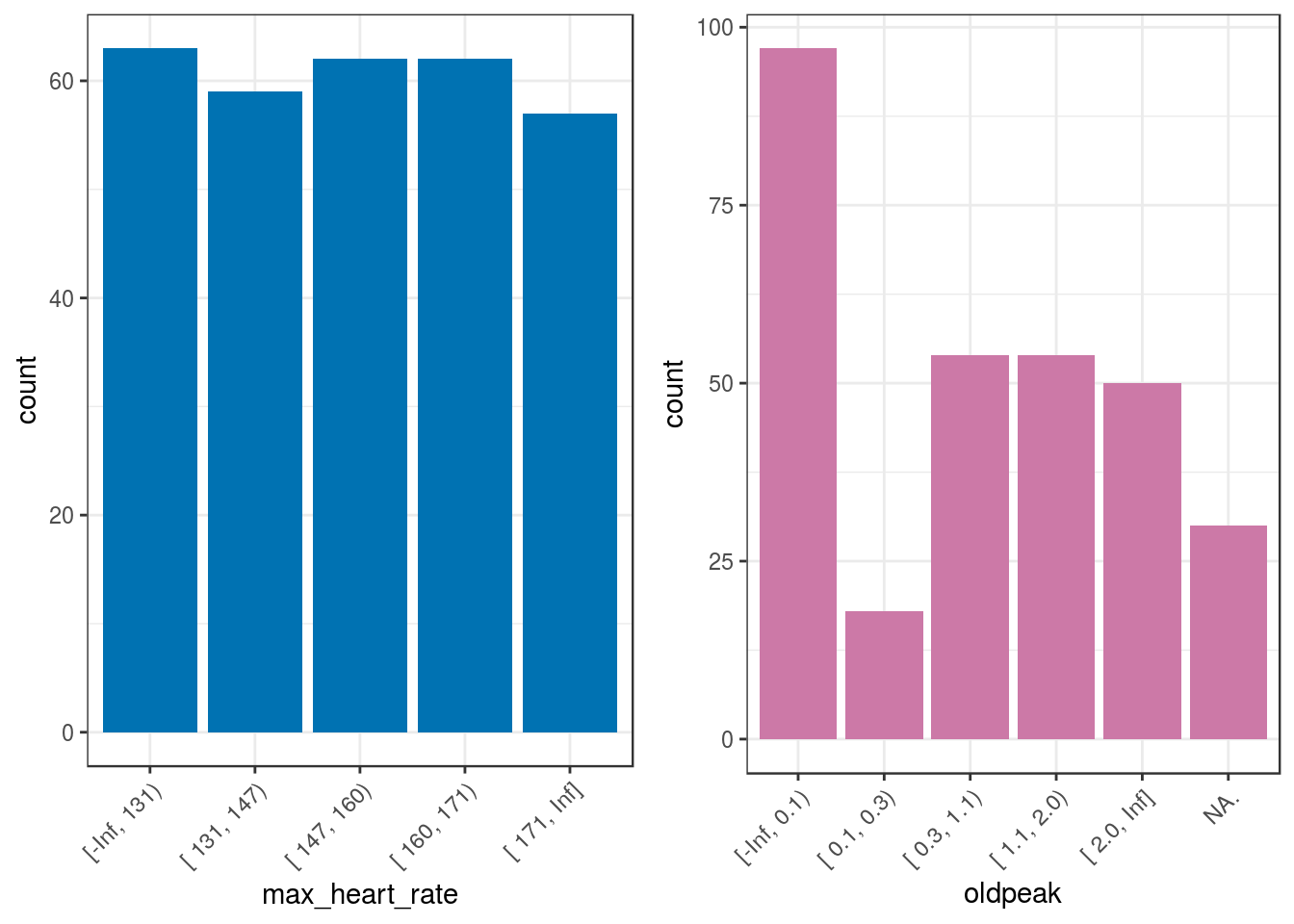
Figure 2.7: Resultados de la discretización automática
A veces, no es posible obtener la misma cantidad de casos por segmento al computar por igual frecuencia, como en el caso de la variable oldpeak.
2.1.9.2 Manejo de valores NA
Con respecto a los valores NA, la nueva variable oldpeak tiene seis categorías: cinco categorías definidas en n_bins=5 más el valor NA. Noten el punto al final que indica la presencia de valores faltantes.
2.1.9.3 Más información
discretize_dfnunca devolverá un valorNAsin transformarlo en el stringNA..n_binsconfigura la cantidad de segmentos para todas las variables.- Si falta
input, entonces correrá para todas las variables numéricas o enteras en las que la cantidad de valores únicos sea mayor que la cantidad de segmentos (n_bins). - Solo las variables definidas en
inputserán procesadas, mientras que las restantes no serán modificadas en absoluto. discretize_get_binsdevuelve un data frame que puede ser modificado a mano como sea necesario, ya sea en un archivo de texto o en la sesión de R.
2.1.9.4 Discretización con nuevos datos
En nuestros datos, el valor mínimo para max_heart_rate es 71. La preparación de datos debe ser robusta cuando incorporamos nuevos casos; por ejemplo, si llega un nuevo paciente cuya max_heart_rate es 68, entonces el proceso actual lo asignará a la categoría más baja.
En otras funciones de otros paquetes, esta preparación puede devolver un NA porque está fuera del segmento.
Como señalamos anteriormente, si los nuevos datos llegan a lo largo del tiempo, es probable que obtengan nuevos valores mínimos/máximos. Esto puede romper nuestro proceso. Para resolver esto, discretize_df siempre tendrá como mínimo/máximo los valores -Inf/Inf; por lo tanto, cualquier nuevo valor que caiga por debajo o por encima del mínimo/máximo se añadirá al segmento más bajo o más alto según corresponda.
El data frame devuelto por discretize_get_bins debe ser guardado para poder aplicarlo a nuevos datos. Si la discretización no está pensada para funcionar con nuevos datos, entonces no tiene sentido tener dos funciones: puede ser solo una. Además, no habría necesidad de guardar los resultados de discretize_get_bins.
Con este enfoque de dos pasos, podemos manejar ambos casos.
2.1.9.5 Conclusiones sobre la discretización de dos pasos
El uso de discretize_get_bins + discretize_df permite una rápida preparación de datos, con un data frame limpio y listo para usar. Dado que muestra claramente dónde empieza y termina cada segmento, resulta indispensable a la hora de realizar informes estadísticos.
La decisión de no fallar a la hora de manejar un nuevo valor mínimo o máximo cuando incorporamos nuevos datos es solo una decisión. En algunos contextos, fracasar puede ser el comportamiento deseado.
La intervención humana: La manera más fácil de discretizar un data frame es seleccionar la misma cantidad de segmentos para aplicar a cada variable, igual que en el ejemplo que vimos. Sin embargo, si es necesario realizar ajustes, entonces algunas variables pueden necesitar un número diferente de segmentos. Por ejemplo, una variable con menos dispersión puede funcionar bien con pocos segmentos.
Los valores más comunes para el número de segmentos suelen ser 3, 5, 10 ó 20 (pero no más). Esta decisión corre por cuenta del científico de datos.
2.1.9.6 Bonus track: El arte del equilibrio ⚖️
- Alta cantidad de segmentos => Más ruido capturado
- Baja cantidad de segmentos => Demasiada simplificación, menos varianza.
¿Estos términos les suenan parecidos a otros empleados en el ámbito de machine learning?
La respuesta: ¡Sí! Solo por mencionar un ejemplo: buscar el equilibrio a la hora de agregar o quitar variables en un modelo predictivo.
- Más variables: Alerta de sobreajuste (el modelo predictivo es demasiado detallado).
- Menos variables: Peligro de subajuste (no hay suficiente información para captar los patrones generales).
Como la filosofía oriental ha señalado durante miles de años, hay un arte en encontrar el equilibrio justo entre un valor y su opuesto.
2.1.10 Reflexiones finales
Como podemos ver, cada decisión tiene su costo en la discretización o preparación de datos. ¿Cómo creen que un sistema automático o inteligente resolverá todas estas situaciones sin la intervención o el análisis humano?
Para estar seguros, podemos delegar algunas tareas a procesos automáticos; sin embargo, los humanos son indispensables en la etapa de preparación de datos, brindando los datos de entrada correctos para procesar.
La asignación de variables como categóricas o numéricas, los dos tipos de datos más utilizados, varía según la naturaleza de los datos y los algoritmos seleccionados, ya que algunos sólo soportan un tipo de datos.
La conversión introduce algún sesgo al análisis. Un caso similar existe cuando se trata de valores faltantes: Manejo e imputación de datos faltantes.
Cuando trabajamos con variables categóricas, podemos cambiar su distribución reorganizando las categorías según una variable objetivo para exponer mejor su relación. Convertir una relación variable no lineal en una lineal.
2.1.11 Bonus track 💥
Volvamos a la sección sobre discretización de variables y grafiquemos todas las transformaciones que hemos visto hasta ahora:
grid.arrange(p2, p3, p4, ncol = 3)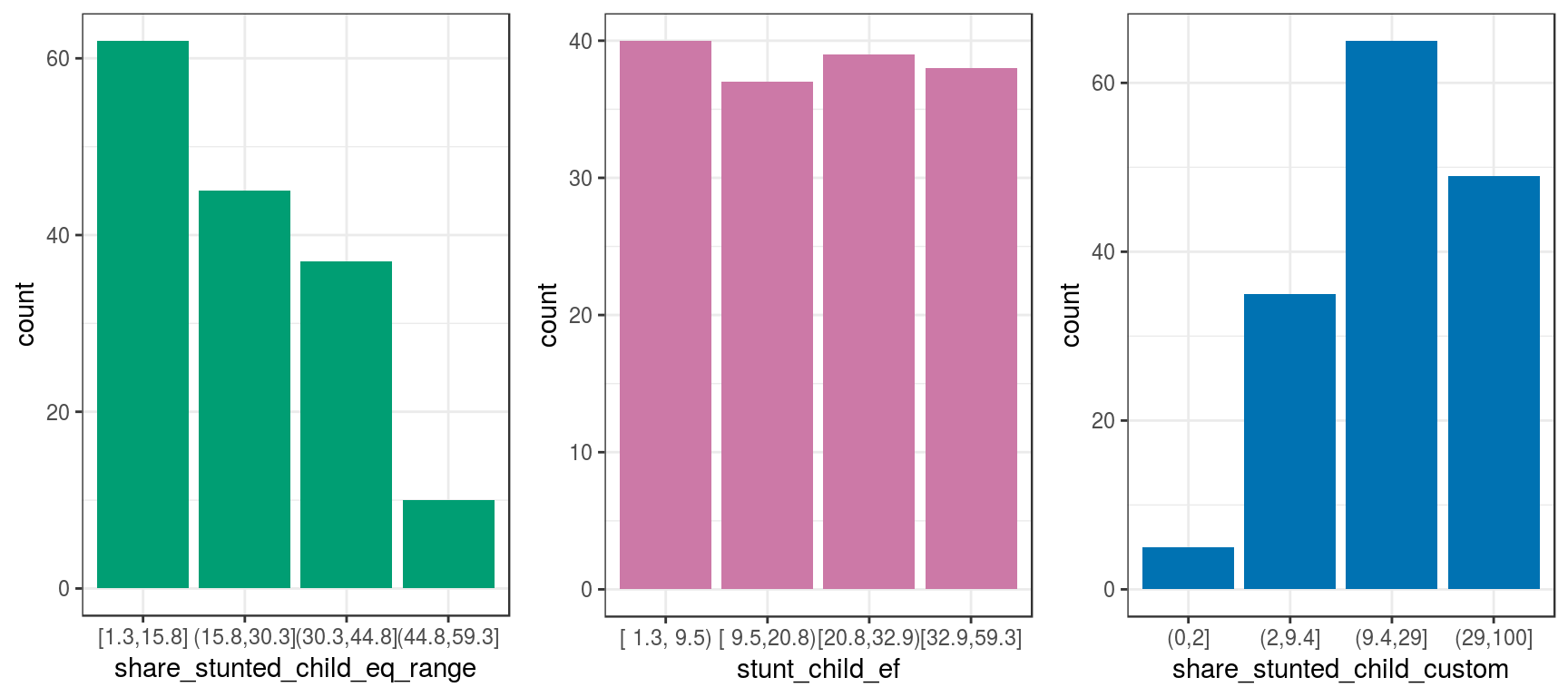
Figure 2.8: Mismos datos, diferentes visualizaciones
Los datos ingresados son siempre los mismos. Sin embargo, todos estos métodos exhiben diferentes perspectivas de la misma cosa.
Algunas perspectivas son más adecuadas que otras para ciertas situaciones, como el uso de igual frecuencia para modelos predictivos.
Aunque este caso solo considera una variable, el razonamiento es el mismo si tenemos más variables a la vez, es decir, un espacio “N-dimensional”.
Cuando construimos modelos predictivos, describimos el mismo grupo de puntos de diferentes maneras, al igual que cuando distintas personas dan su opinión sobre un objeto.

2.2 Variables de alta cardinalidad en estadística descriptiva
2.2.1 ¿De qué se trata esto?
Una variable de alta cardinalidad es aquella que puede tomar muchos valores diferentes. Por ejemplo, la variable país.
Este capítulo cubrirá la reducción de la cardinalidad basada en la regla de Pareto, usando la función freq que da una visión rápida sobre dónde se concentran la mayoría de los valores y la distribución de la variable.
2.2.2 Alta cardinalidad en estadística descriptiva
El siguiente ejemplo contiene una encuesta de 910 casos, con 3 columnas: person, country y has_flu, que indica haber tenido gripe en el último mes.
library(funModeling) Los datos de data_country están incluidos en el paquete funModeling (por favor actualicen a la versión 1.6).
Rápido análisis numérico de data_country (primeras 10 filas)
# Graficar las primeras 10 filas
head(data_country, 10)## person country has_flu
## 478 478 France no
## 990 990 Brazil no
## 606 606 France no
## 575 575 Philippines no
## 806 806 France no
## 232 232 France no
## 422 422 Poland no
## 347 347 Romania no
## 858 858 Finland no
## 704 704 France no# Explorar los datos, visualizando solamente las primeras 10 filas
head(freq(data_country, "country"), 10)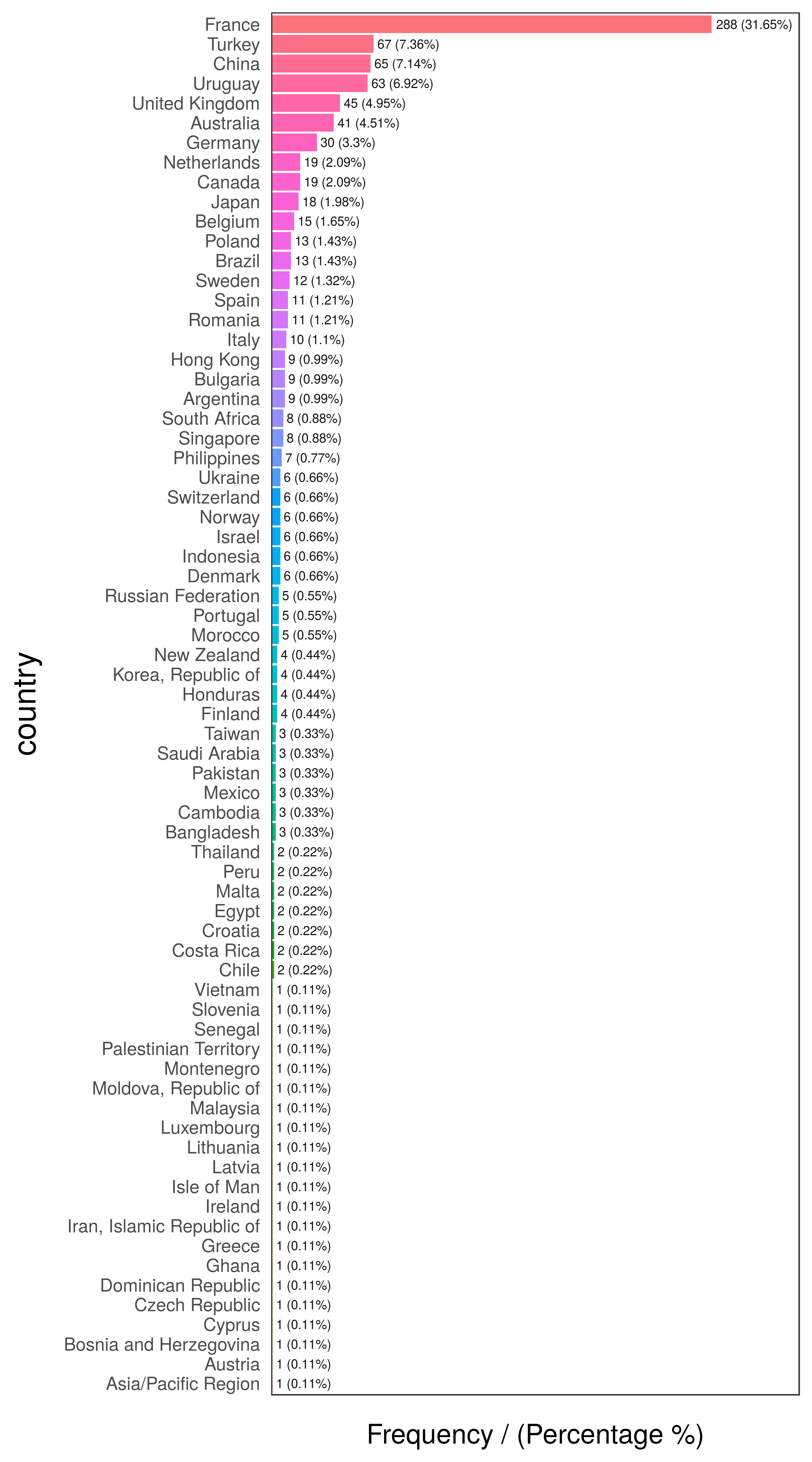
Figure 2.9: Análisis de frecuencia por país
## country frequency percentage cumulative_perc
## 1 France 288 31.65 31.65
## 2 Turkey 67 7.36 39.01
## 3 China 65 7.14 46.15
## 4 Uruguay 63 6.92 53.07
## 5 United Kingdom 45 4.95 58.02
## 6 Australia 41 4.51 62.53
## 7 Germany 30 3.30 65.83
## 8 Canada 19 2.09 67.92
## 9 Netherlands 19 2.09 70.01
## 10 Japan 18 1.98 71.99# Explorar los datos
freq(data_country, "has_flu")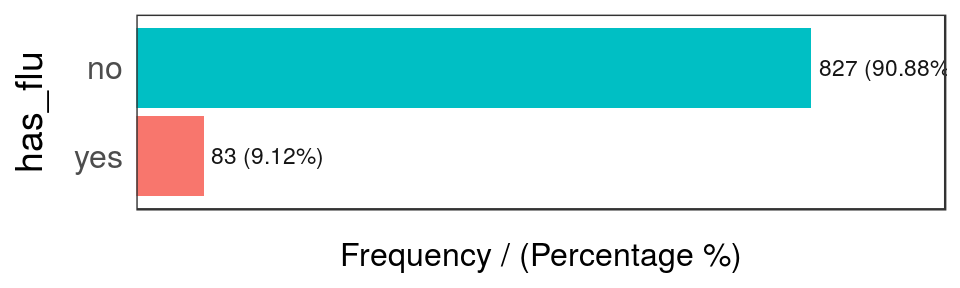
Figure 2.10: Análisis de frecuencia de casos con gripe
## has_flu frequency percentage cumulative_perc
## 1 no 827 90.88 90.88
## 2 yes 83 9.12 100.00La última tabla muestra que hay sólo 83 filas en las que has_flu="yes", lo que representa cerca del 9% del total de personas (que tuvieron gripe).
Pero muchos de ellos casi no tienen participación en los datos. Esta es la cola larga, por lo que una técnica para reducir la cardinalidad es conservar aquellas categorías que están presentes en un alto porcentaje de los datos, por ejemplo 70, 80 o 90%, el principio de Pareto.
# La función 'freq', del paquete 'funModeling', recupera el porcentaje acumulado que nos ayudará a hacer el corte.
country_freq=freq(data_country, 'country', plot = F)
# Dado que 'country_freq' es una tabla ordenada por frecuencia, inspeccionemos las primeras 10 filas que tienen la mayor participación.
country_freq[1:10,]## country frequency percentage cumulative_perc
## 1 France 288 31.65 31.65
## 2 Turkey 67 7.36 39.01
## 3 China 65 7.14 46.15
## 4 Uruguay 63 6.92 53.07
## 5 United Kingdom 45 4.95 58.02
## 6 Australia 41 4.51 62.53
## 7 Germany 30 3.30 65.83
## 8 Canada 19 2.09 67.92
## 9 Netherlands 19 2.09 70.01
## 10 Japan 18 1.98 71.99Vemos que 10 representan más del 70% de los casos. Podemos asignar la categoría other a los casos restantes y graficar:
data_country$country_2=ifelse(data_country$country %in% country_freq[1:10,'country'], data_country$country, 'other')
freq(data_country, 'country_2')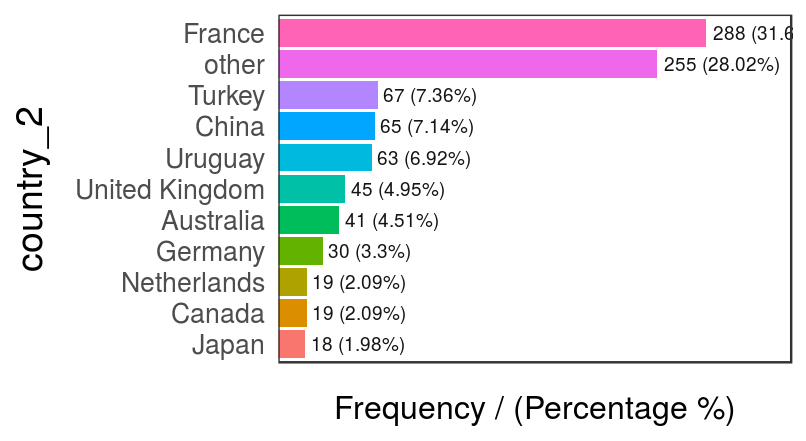
Figure 2.11: Variable país modificada - análisis de frecuencia
## country_2 frequency percentage cumulative_perc
## 1 France 288 31.65 31.65
## 2 other 255 28.02 59.67
## 3 Turkey 67 7.36 67.03
## 4 China 65 7.14 74.17
## 5 Uruguay 63 6.92 81.09
## 6 United Kingdom 45 4.95 86.04
## 7 Australia 41 4.51 90.55
## 8 Germany 30 3.30 93.85
## 9 Canada 19 2.09 95.94
## 10 Netherlands 19 2.09 98.03
## 11 Japan 18 1.98 100.002.2.3 Comentarios finales
Las categorías poco representativas a veces son errores en los datos, como tener: “Egipto”, “Eggipto.”, y pueden dar alguna evidencia de malos hábitos de recolección de datos y/o posibles errores en la recolección de la fuente.
No existe una regla general para reducir los datos, depende de cada caso particular.
Próximo capítulo recomendado: Variables de alta cardinalidad en modelado predictivo

2.3 Variables de alta cardinalidad en modelado predictivo
2.3.1 ¿De qué se trata esto?
Como hemos visto en el capítulo anterior, Alta cardinalidad en estadística descriptiva, conservamos las categorías con la mayor representatividad, pero ¿qué tal si podemos tener otra variable para predecir con ella? Es decir, predecir has_flu basándonos en country.
Utilizar el último método puede destruir la información de la variable, por lo que pierde poder predictivo. En este capítulo iremos más allá en el método descrito anteriormente, utilizando una función de agrupación automática -auto_grouping- y navegando a través de la estructura de la variable para dar algunas ideas sobre cómo optimizar una variable categórica, pero lo más importante: animar al lector a realizar sus propias optimizaciones.
Otros autores han nombrado este reagrupamiento como reducción de la cardinalidad o encoding.
¿Qué vamos a repasar en este capítulo?
- Concepto de representatividad de los datos (tamaño de muestra).
- Tamaño de muestra con una variable objetivo o de resultado.
- De R: Presentar un método para ayudar a reducir la cardinalidad y analizar numéricamente variables categóricas.
- Un ejemplo práctico de antes y después que reduce la cardinalidad y facilita la extracción de ideas.
- Cómo diferentes modelos, como un random forest o gradient boosting machine (GBM, en inglés), manejan las variables categóricas.
2.3.2 Pero, ¿es necesario reagrupar la variable?
Depende del caso, pero la respuesta más rápida es sí. En este capítulo veremos un caso en el que esta preparación de datos aumenta la precisión general (medida por área debajo de la curva ROC).
Existe un equilibrio entre la representación de los datos (cuántas filas tiene cada categoría) y cómo se relaciona cada categoría con la variable de resultado. Por ejemplo: algunos países son más propensos a los casos de gripe que otros.
# Cargar funModeling >=1.6 que contiene todas las funciones para lidiar con esto.
library(funModeling)
library(dplyr)Analizamos numéricamente data_country, que viene en el paquete funModeling (por favor actualicen a la versión > 1.6.5).
Análisis rápido de data_country (primeras 10 filas)
# Graficar las primeras 10 filas
head(data_country, 10)## person country has_flu country_2
## 478 478 France no France
## 990 990 Brazil no other
## 606 606 France no France
## 575 575 Philippines no other
## 806 806 France no France
## 232 232 France no France
## 422 422 Poland no other
## 347 347 Romania no other
## 858 858 Finland no other
## 704 704 France no France# Explorar los datos, visualizando solamente las primeras 10 filas
head(freq(data_country, "country"), 10)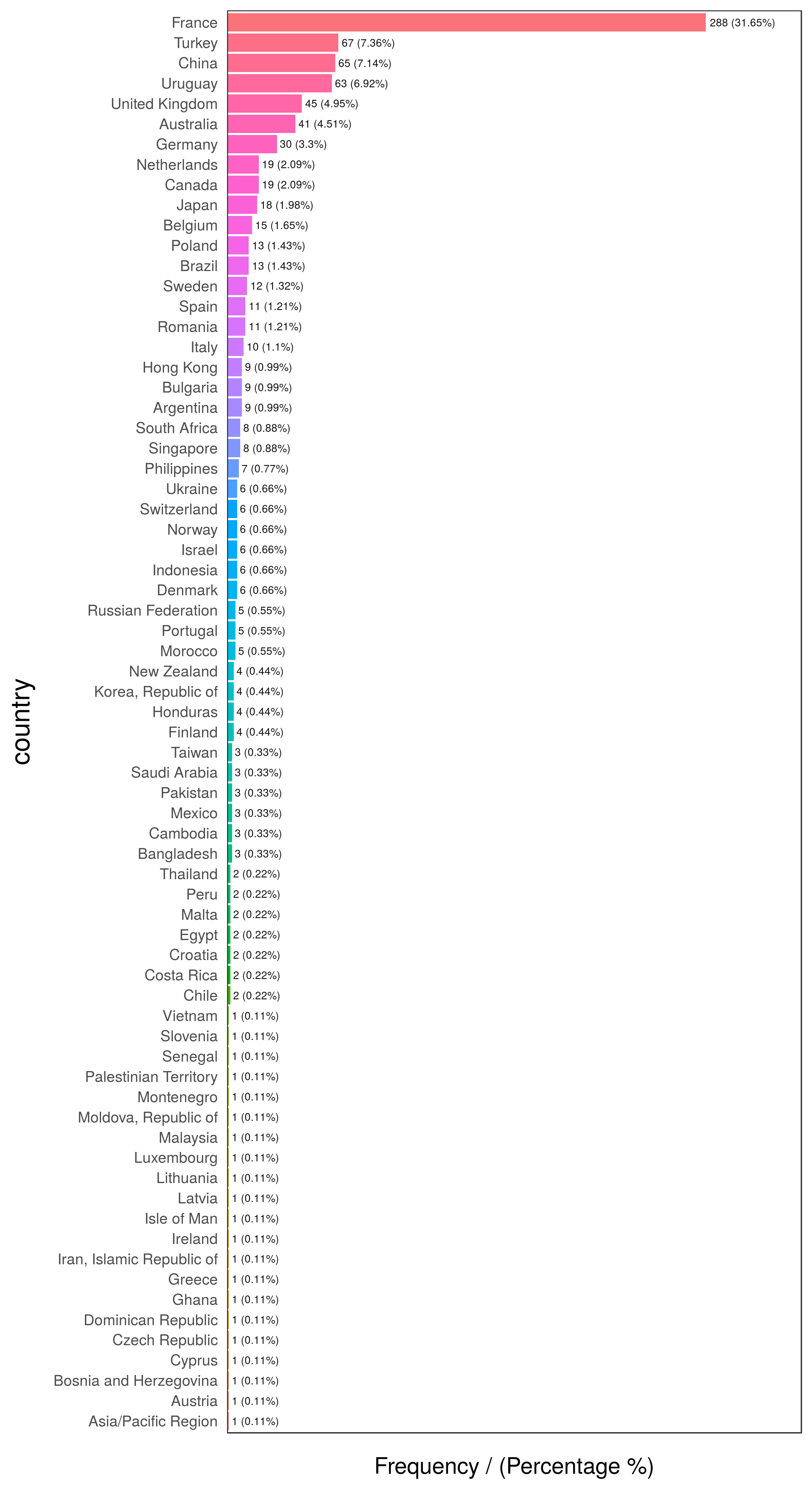
Figure 2.12: Primeros 10 países
## country frequency percentage cumulative_perc
## 1 France 288 31.65 31.65
## 2 Turkey 67 7.36 39.01
## 3 China 65 7.14 46.15
## 4 Uruguay 63 6.92 53.07
## 5 United Kingdom 45 4.95 58.02
## 6 Australia 41 4.51 62.53
## 7 Germany 30 3.30 65.83
## 8 Canada 19 2.09 67.92
## 9 Netherlands 19 2.09 70.01
## 10 Japan 18 1.98 71.99# Explorar los datos
freq(data_country, "has_flu")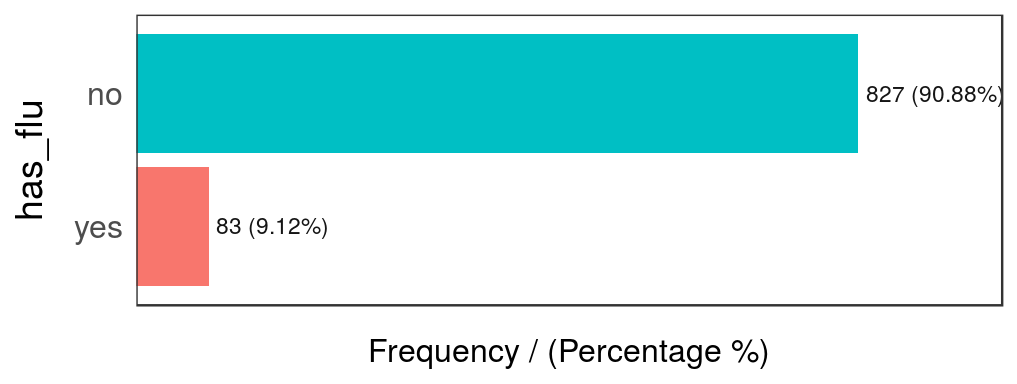
Figure 2.13: Distribucíón de la variable has flu
## has_flu frequency percentage cumulative_perc
## 1 no 827 90.88 90.88
## 2 yes 83 9.12 100.002.3.3 El caso 🔍
El modelo predictivo intentará mapear ciertos valores con ciertos resultados, en nuestro caso la variable objetivo es binaria.
Calcularemos un análisis numérico completo de country con respecto a la variable objetivo has_flu basado en categ_analysis.
Cada fila representa una categoría única de variables input. Y en cada fila podemos encontrar atributos que definen cada categoría en términos de representatividad y probabilidad.
# `categ_analysis` está disponible en "funModeling" >= v1.6, por favor instalen esta versión antes de usarla.
country_profiling=categ_analysis(data=data_country, input="country", target = "has_flu")
# Visualizar las primeras 15 filas (países) de 70.
head(country_profiling, 15)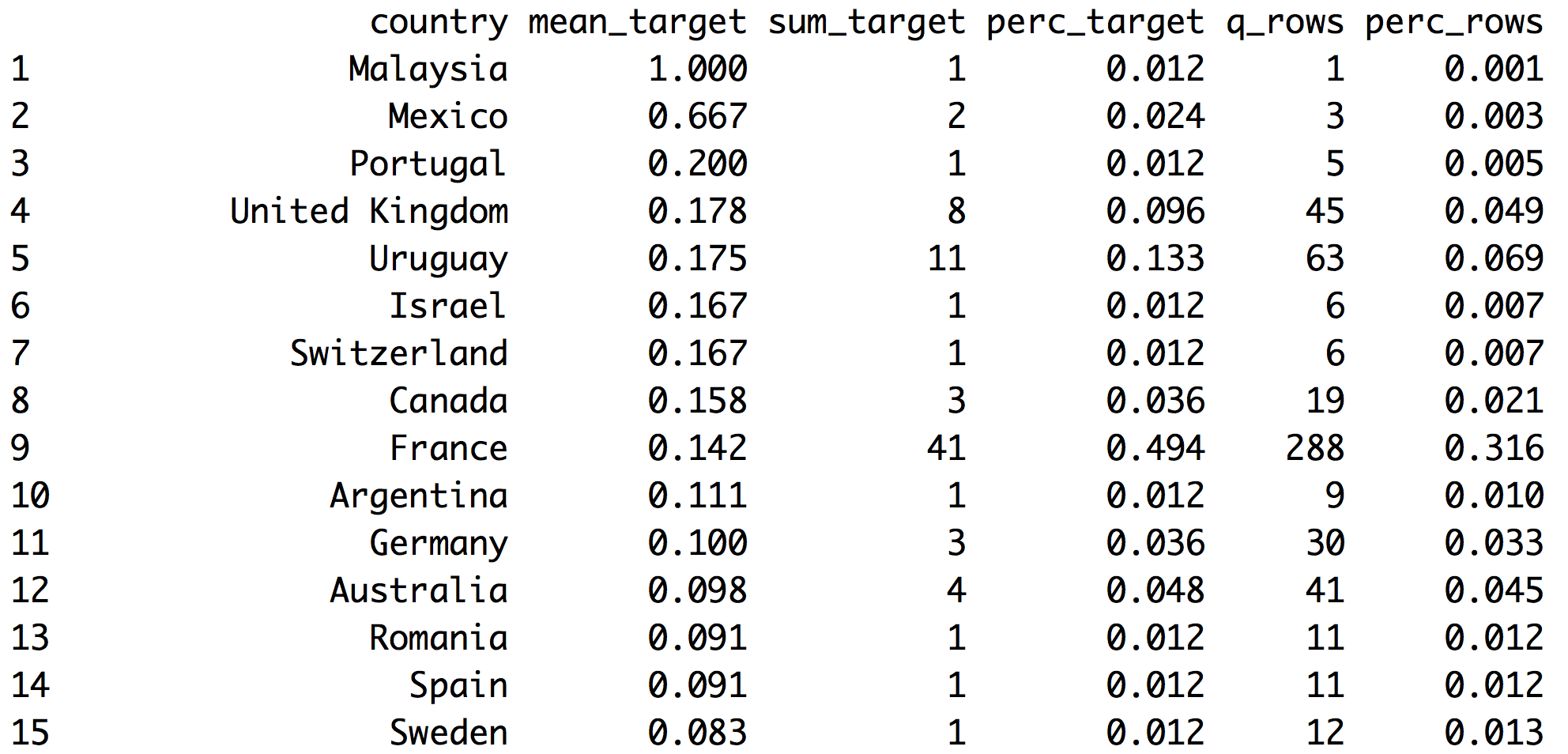
Figure 2.14: Analizando el objetivo vs. los datos ingresados
- Nota 1: La primera columna ajusta automáticamente su nombre en base a la variable
input - Nota 2: La variable
has_flutiene valoresyesyno,categ_analysisasigna internamente el número 1 a la clase menos representativa,yesen este caso, para calcular el promedio, suma y porcentaje.
Estas son las métricas que devuelve categ_analysis:
country: nombre de cada categoría en la variableinput.mean_target:sum_target/q_rows, número promedio dehas_flu="yes"para una categoría. Esta es la probabilidad.sum_target: cantidad de valoreshas_flu="yes"en cada categoría.perc_target: lo mismo quesum_targetpero expresado como porcentaje,sum_target of each category / total sum_target. Esta columna suma1.00.q_rows: cantidad de filas que, más allá de la variablehas_flu, cayeron en una categoría. Es la distribución deinput. Esta columna suma la cantidad total de filas analizadas.perc_rows: relacionado conq_rows, representa la porción o porcentaje de cada categoría. Esta columna suma1.00.
2.3.3.1 ¿Qué conclusiones podemos extraer de esto?
Leyendo como ejemplo la primera fila de France:
- 41 personas tienen gripe (
sum_target=41). Estas 41 personas representan casi el 50% del total de personas con gripe (perc_target=0.494). - La probabilidad de tener gripe en Francia es 14.2% (
mean_target=0.142) - Total de filas de Francia=288 -de 910-. Esta es la variable
q_rows;perc_rowses el mismo número pero en porcentaje.
Sin considerar el filtro por país, tenemos:
- La columna
sum_targetsuma el total de personas con gripe en los datos actuales. - La columna
perc_targetsuma1.00-o 100% - La columna
q_rowssuma el total de filas presentes en el data framedata_country. - La columna
perc_rowssuma1.00o 100%.
2.3.4 Análisis para el modelado predictivo 🔮
Cuando desarrollamos modelos predictivos, puede que nos interesen aquellos valores que aumentan la probabilidad de un determinado evento. En nuestro caso:
¿Cuáles son los países que maximizan la probabilidad de encontrar personas con gripe?
Fácil, tomemos country_profiling en orden descendiente según mean_target:
# Ordenar country_profiling por mean_target y luego tomar los primeros 6 países
arrange(country_profiling, -mean_target) %>% head(.)## country mean_target sum_target perc_target q_rows perc_rows
## 1 Malaysia 1.000 1 0.012 1 0.001
## 2 Mexico 0.667 2 0.024 3 0.003
## 3 Portugal 0.200 1 0.012 5 0.005
## 4 United Kingdom 0.178 8 0.096 45 0.049
## 5 Uruguay 0.175 11 0.133 63 0.069
## 6 Israel 0.167 1 0.012 6 0.007¡Genial! Tenemos a Malasyia como el país con mayor probabilidad de tener gripe! El 100% de las personas ahí tienen gripe (mean_has_flu=1.000).
Pero nuestro sentido común nos aconseja que quizás algo anda mal….
¿Cuántas filas tiene Malasyia? Respuesta: 1. -columna: q_rows=1 ¿Cuántos casos positivos tiene Malasyia? Respuesta: 1 -columna: sum_target=1.
Dado que no se puede aumentar la muestra vean que si esta proporción se mantiene alta, contribuirá a un sobreajuste y creará un sesgo en el modelo predictivo.
¿Y qué pasa con Mexico? 2 de cada 3 tienen gripe…. todavía parece baja. Sin embargo, Uruguay tiene un 17,3% de probabilidad -11 de 63 casos- y estos 63 casos representan casi el 7% de la población total (perc_row=0,069), esta proporción parece más creíble.
A continuación se presentan algunas ideas para tratar esto:
2.3.4.1 Caso 1: Reducción mediante la recategorización de valores menos representativos
Mantengamos todos los casos que tengan al menos un determinado porcentaje de representación en los datos. Supongamos que cambiamos el nombre de los países que tienen menos del 1% de presencia en los datos a others.
country_profiling=categ_analysis(data=data_country, input="country", target = "has_flu")
countries_high_rep=filter(country_profiling, perc_rows>0.01) %>% .$country
# Si no pertenece a countries_high_rep entonces lo asignamos a la categoría `other`
data_country$country_new=ifelse(data_country$country %in% countries_high_rep, data_country$country, "other")Volvemos a chequear la probabilidad:
country_profiling_new=categ_analysis(data=data_country, input="country_new", target = "has_flu")
country_profiling_new## country_new mean_target sum_target perc_target q_rows perc_rows
## 1 United Kingdom 0.178 8 0.096 45 0.049
## 2 Uruguay 0.175 11 0.133 63 0.069
## 3 Canada 0.158 3 0.036 19 0.021
## 4 France 0.142 41 0.494 288 0.316
## 5 Germany 0.100 3 0.036 30 0.033
## 6 Australia 0.098 4 0.048 41 0.045
## 7 Romania 0.091 1 0.012 11 0.012
## 8 Spain 0.091 1 0.012 11 0.012
## 9 Sweden 0.083 1 0.012 12 0.013
## 10 Netherlands 0.053 1 0.012 19 0.021
## 11 other 0.041 7 0.084 170 0.187
## 12 Turkey 0.030 2 0.024 67 0.074
## 13 Belgium 0.000 0 0.000 15 0.016
## 14 Brazil 0.000 0 0.000 13 0.014
## 15 China 0.000 0 0.000 65 0.071
## 16 Italy 0.000 0 0.000 10 0.011
## 17 Japan 0.000 0 0.000 18 0.020
## 18 Poland 0.000 0 0.000 13 0.014Hemos reducido drásticamente la cantidad de países -74% menos- sólo reduciendo la cantidad de países al recategorizar al 1% menos representativo. Quedaron 18 de los 70 países.
La probabilidad de una variable objetivo se ha estabilizado un poco más en la categoría “otra”. Ahora cuando el modelo predictivo vea Malasyia no asignará el 100% de la probabilidad, sino el 4.1% (mean_has_flu=0.041).
Consejo sobre este último método
Tengan cuidado al aplicar esta técnica a ciegas. A veces, en una predicción objetivo altamente desequilibrada -por ejemplo, detección de anomalías- el comportamiento anormal está presente en menos del 1% de los casos.
# Replicar los datos
d_abnormal=data_country
# Simular comportamiento anormal en algunos países
d_abnormal$abnormal=ifelse(d_abnormal$country %in% c("Brazil", "Chile"), 'yes', 'no')
# Análisis categórico
ab_analysis=categ_analysis(d_abnormal, input = "country", target = "abnormal")
# Visualizar sólo los primeros 6 elementos
head(ab_analysis)## country mean_target sum_target perc_target q_rows perc_rows
## 1 Brazil 1 13 0.867 13 0.014
## 2 Chile 1 2 0.133 2 0.002
## 3 Argentina 0 0 0.000 9 0.010
## 4 Asia/Pacific Region 0 0 0.000 1 0.001
## 5 Australia 0 0 0.000 41 0.045
## 6 Austria 0 0 0.000 1 0.001# Inspeccionar la distribución, sólo unos pocos pertenecen a la categoría 'no'
freq(d_abnormal, "abnormal", plot = F)## abnormal frequency percentage cumulative_perc
## 1 no 895 98.35 98.35
## 2 yes 15 1.65 100.00¿Cuántos valores anormales hay?
Sólo 15, y representan el 1,65% de los valores totales.
Comprobando la tabla devuelta por categ_analysis, podemos ver que este comportamiento anormal ocurre sólo en categorías con una participación realmente baja: Brazil que está presente en sólo 1,4% de los casos, y Chile con 0,2%.
En este caso, crear una categoría other basada en la distribución no es una buena idea.
Conclusión:
A pesar de que este es un ejemplo preparado, hay algunas técnicas de preparación de datos que pueden ser realmente útiles en términos de precisión, pero necesitan cierta supervisión. Esta supervisión puede ser con ayuda de algoritmos.
2.3.4.2 Caso 2: Reducción mediante agrupación automática
Este procedimiento utiliza la técnica de clustering o agrupamiento kmeans y la tabla devuelta por categ_analysis para crear grupos -clusters- que contienen categorías que muestran un comportamiento similar en términos de:
perc_rowsperc_target
La combinación de ambos nos llevará a encontrar grupos en base a la probabilidad y la representatividad.
Manos a la obra en R:
Definimos el parámetro n_groups, es el número de grupos deseados. El número es relativo a los datos y a la cantidad de categorías totales. Pero un número general estaría entre 3 y 10.
La función auto_grouping está incluida en funModeling >=1.6. Por favor noten que el parámetro target sólo funciona para variables no binarias.
Note: el parámetro seed es opcional, pero al asignarle un número siempre obtendrá los mismos resultados.
# Reducir la cardinalidad
country_groups=auto_grouping(data = data_country, input = "country", target="has_flu", n_groups=9, seed = 999)
country_groups$df_equivalence## country country_rec
## 1 Australia group_1
## 2 Canada group_1
## 3 Germany group_1
## 4 France group_2
## 5 China group_3
## 6 Turkey group_3
## 7 Asia/Pacific Region group_4
## 8 Austria group_4
## 9 Bangladesh group_4
## 10 Bosnia and Herzegovina group_4
## 11 Cambodia group_4
## 12 Chile group_4
## 13 Costa Rica group_4
## 14 Croatia group_4
## 15 Cyprus group_4
## 16 Czech Republic group_4
## 17 Dominican Republic group_4
## 18 Egypt group_4
## 19 Ghana group_4
## 20 Greece group_4
## 21 Iran, Islamic Republic of group_4
## 22 Ireland group_4
## 23 Isle of Man group_4
## 24 Latvia group_4
## 25 Lithuania group_4
## 26 Luxembourg group_4
## 27 Malta group_4
## 28 Moldova, Republic of group_4
## 29 Montenegro group_4
## 30 Pakistan group_4
## 31 Palestinian Territory group_4
## 32 Peru group_4
## 33 Saudi Arabia group_4
## 34 Senegal group_4
## 35 Slovenia group_4
## 36 Taiwan group_4
## 37 Thailand group_4
## 38 Vietnam group_4
## 39 Belgium group_5
## 40 Brazil group_5
## 41 Bulgaria group_5
## 42 Hong Kong group_5
## 43 Italy group_5
## 44 Poland group_5
## 45 Singapore group_5
## 46 South Africa group_5
## 47 Argentina group_6
## 48 Israel group_6
## 49 Malaysia group_6
## 50 Mexico group_6
## 51 Portugal group_6
## 52 Romania group_6
## 53 Spain group_6
## 54 Sweden group_6
## 55 Switzerland group_6
## 56 Japan group_7
## 57 Netherlands group_7
## 58 United Kingdom group_8
## 59 Uruguay group_8
## 60 Denmark group_9
## 61 Finland group_9
## 62 Honduras group_9
## 63 Indonesia group_9
## 64 Korea, Republic of group_9
## 65 Morocco group_9
## 66 New Zealand group_9
## 67 Norway group_9
## 68 Philippines group_9
## 69 Russian Federation group_9
## 70 Ukraine group_9auto_grouping devuelve una lista que contiene 3 objetos:
df_equivalence: data frame que contiene una tabla para encontrar las equivalencias entre datos viejos y nuevos.fit_cluster: modelo k-means que se utiliza para reducir la cardinalidad (los valores se escalan).recateg_results: data frame que contiene el análisis numérico de cada grupo con respecto a la variable objetivo. La primera columna ajusta su nombre a la variable de entrada. En este caso tenemos:country_rec. Cada grupo corresponde a una o varias categorías de la variable de entrada (como vimos endf_equivalence).
Exploremos cómo se comportan los nuevos grupos, esto es lo que verá el modelo predictivo:
country_groups$recateg_results## country_rec mean_target sum_target perc_target q_rows perc_rows
## 1 group_8 0.176 19 0.229 108 0.119
## 2 group_6 0.156 10 0.120 64 0.070
## 3 group_2 0.142 41 0.494 288 0.316
## 4 group_1 0.111 10 0.120 90 0.099
## 5 group_7 0.027 1 0.012 37 0.041
## 6 group_3 0.015 2 0.024 132 0.145
## 7 group_4 0.000 0 0.000 49 0.054
## 8 group_5 0.000 0 0.000 85 0.093
## 9 group_9 0.000 0 0.000 57 0.063La última tabla está ordenada por mean_target, por lo que podemos ver rápidamente los grupos según probabilidad máxima o mínima:
group_2es el más común, está presente en el 31.6% de los casos y el valor demean_target(probabilidad) es 14.2%.group_8tiene la probabilidad más alta (17.6%), seguido porgroup_6que tiene una probabilidad de 15.6% de tener un caso positivo (has_flu="yes").group_4,group_5ygroup_9se ven iguales. Pueden ser un mismo grupo, dado que la probabiliad es 0 en todos los casos.group_7ygroup_3tienen 1 y 2 países con casos positivos. Podríamos considerar estos números como uno solo, juntándolos en un solo grupo, que eventualmente representará a los países con la probabilidad más baja.
Primero debemos agregar la columna de la nueva categoría al conjunto de datos original.
data_country_2=data_country %>% inner_join(country_groups$df_equivalence, by="country")Ahora hacemos las transformaciones adicionales reemplazando:
group_4,group_5ygroup_9seránlow_likelihood, (países sin casos positivos o con bajo porcentaje de la variable objetivo).group_7ygroup_3seránlow_target_share.
data_country_2$country_rec=
ifelse(data_country_2$country_rec %in%
c("group_4", "group_5", "group_9"),
"low_likelihood",
data_country_2$country_rec
)
data_country_2$country_rec=
ifelse(data_country_2$country_rec %in%
c("group_7", "group_3"),
"low_target_share",
data_country_2$country_rec
)Verificando la agrupación final (variable country_rec):
categ_analysis(data=data_country_2, input="country_rec", target = "has_flu")## country_rec mean_target sum_target perc_target q_rows perc_rows
## 1 group_8 0.176 19 0.229 108 0.119
## 2 group_6 0.156 10 0.120 64 0.070
## 3 group_2 0.142 41 0.494 288 0.316
## 4 group_1 0.111 10 0.120 90 0.099
## 5 low_target_share 0.018 3 0.036 169 0.186
## 6 low_likelihood 0.000 0 0.000 191 0.210Cada grupo parece tener un buen tamaño de muestra con respecto a la distribución de sum_target. Nuestra transformación dejó a low_likelihood con una representación del 21% del total de casos, aún con 0 casos positivos (sum_target=0). Y low_target_share con 3 casos positivos, lo que representa el 3.6% de los casos positivos.
Todos los grupos parecen tener una buena representación. Esto se puede comprobar en la variable perc_rows. Todos los casos están por encima del 7%.
Intentar con un número menor de clusters puede ayudar a reducir un poco esta tarea manual. Esto fue sólo una demostración de cómo optimizar una variable que tiene muchas categorías diferentes.
2.3.5 Manejo de nuevas categorías cuando el modelo predictivo está en producción
Imaginemos que aparece un nuevo país, new_country_hello_world, los modelos predictivos fallarán ya que fueron entrenados con valores fijos. Una técnica es asignar un grupo que tenga mean_target=0.
Es similar al caso del último ejemplo. Pero la diferencia está en group_5: esta categoría encajaría mejor en un grupo de probabilidad media que en un valor completamente nuevo.
Después de un tiempo deberíamos reconstruir el modelo con todos los nuevos valores, de lo contrario estaríamos penalizando a new_country_hello_world si tiene una buena probabilidad.
En otras palabras:
¿Aparece una nueva categoría? Envíenla al grupo menos significativo. Después de un tiempo, vuelvan a analizar su impacto. ¿Tiene una probabilidad media o alta? Cámbienla al grupo más adecuado.
2.3.6 ¿Los modelos predictivos pueden manejan la alta cardinalidad? Parte 1
Sí, y no. Algunos modelos tratan mejor que otros este asunto de la alta cardinalidad. En algunos escenarios, esta preparación de datos puede no ser necesaria. Este libro trata de exponer este tema que, a veces, puede llevar a un mejor modelo.
Ahora, vamos a atravesar este tema construyendo dos modelos predictivos: Máquina de potenciación del gradiente - bastante robusta para muchas entradas de datos diferentes.
El primer modelo no tiene datos tratados, y el segundo ha sido tratado por la función en el paquete funModeling.
Estamos midiendo la precisión basándonos en el área ROC, que oscila entre 0.5 y 1; cuanto más alto sea el número, mejor será el modelo. Vamos a utilizar la validación cruzada para estar seguros del valor. La importancia de la validación cruzada de los resultados se trata en el capítulo Conociendo el error.
# Construir el primer modelo, sin reducir la cardinalidad.
library(caret)
fitControl <- trainControl(method = "cv",
number = 4,
classProbs = TRUE,
summaryFunction = twoClassSummary)
fit_gbm_1 <- train(has_flu ~ country,
data = data_country_2,
method = "gbm",
trControl = fitControl,
verbose = FALSE,
metric = "ROC")
# Obtener el mejor valor de ROC
roc=round(max(fit_gbm_1$results$ROC),2)El área debajo de la curva ROC es (roc): 0.65.
Ahora hacemos el mismo modelo con los mismos parámetros, pero aplicando la preparación de datos que hicimos antes.
# Construir el segundo modelo, basándonos en la variable country_rec
fit_gbm_2 <- train(has_flu ~ country_rec,
data = data_country_2,
method = "gbm",
trControl = fitControl,
verbose = FALSE,
metric = "ROC")
# Obtener el nuevo mejor valor de ROC
new_roc=round(max(fit_gbm_2$results$ROC),2)La nueva curva ROC es (new_roc): 0.71.
Luego calculamos el procentaje de mejora con respecto al primer valor de ROC:
Mejora: ~ 9.23%. ✅
Nada mal, ¿no?
Un breve comentario sobre la última prueba:
Hemos utilizado uno de los modelos más robustos, máquina de potenciación del gradiente, y hemos aumentado el rendimiento. Si probamos otro modelo, por ejemplo regresión logística, que es más sensible a los datos sucios, obtendremos una mayor diferencia entre reducir y no reducir la cardinalidad. Esto se puede comprobar borrando el parámetro verbose=FALSE y cambiando method=glm (glm implica regresión logística).
En lecturas adicionales hay un punto de referencia de diferentes tratamientos para variables categóricas y cómo cada una aumenta o disminuye la precisión.
2.3.7 ¿Los modelos predictivos pueden manejan la alta cardinalidad? Parte 2
Revisemos cómo algunos modelos lidian con esto:
Árboles de decisión: Tienden a seleccionar variables con alta cardinalidad en la parte superior, dándoles más importancia que a otras, en función de la ganancia de información. En la práctica, es una prueba de que está sobreajustado. Este modelo es bueno para ver la diferencia entre reducir o no una variable de alta cardinalidad.
Random forest: al menos en la implementación de R, maneja sólo variables categóricas con por lo menos 52 categorías diferentes. Es muy probable que esta limitación sea para evitar el sobreajuste. Este punto, en conjunción con la naturaleza del algoritmo -crea muchos árboles-, reduce el efecto de un único árbol de decisión al elegir una variable de alta cardinalidad.
Gradient Boosting Machine y Regresión logística: convierten variables categóricas internas en variables flag o dummy. En el ejemplo que vimos sobre los países, implica la creación -interna- de 70 variables flag (así es como caret maneja la fórmula, si queremos mantener la variable original sin los dummies no tenemos que usar una fórmula).
Comprobemos el modelo que creamos antes:
# Verificar el primer modelo...
fit_gbm_1$finalModel## A gradient boosted model with bernoulli loss function.
## 50 iterations were performed.
## There were 69 predictors of which 8 had non-zero influence.Eso es: 69 variables de entrada representan a los países, pero las columnas flag fueron reportadas como no relevantes para la predicción.
Esto está relacionado con Ingeniería de variables. Además, está relacionado con Selección de las mejores variables. Es una práctica muy recomendable seleccionar primero las variables que contienen más información y luego crear el modelo predictivo.
Conclusión: la reducción de la cardinalidad reducirá la cantidad de variables en estos modelos.
2.3.8 Variable objetivo numérica o multinomial 📏
Hasta ahora, el libro sólo cubrió casos donde la variable objetivo era una variable binaria. Está previsto que en el futuro abarque también variables objetivo numéricas y multi-valor.
Sin embargo, si leyeron hasta aquí, puede que quieran explorar por su cuenta teniendo en mente la misma idea. En las variables numéricas, por ejemplo la previsión de page visits en un sitio web, habrá ciertas categorías de la variable de entrada que estarán más relacionadas con un valor alto en las visitas, mientras que hay otras que están más correlacionadas con valores bajos.
Lo mismo ocurre con la variable de salida multinomial, habrá algunas categorías más relacionadas con ciertos valores. Por ejemplo, prediciendo el grado de epidemia: high, mid o low según la ciudad. Habrá algunas ciudades que se correlacionarán más con un alto nivel epidémico que otras.
2.3.9 ¿Qué beneficio “extra” 🎁 obtuvimos con la agrupación?
Saber cómo las categorías fueron asignadas a los grupos nos brinda información que -en algunos casos- es bueno registrar. Las categorías que pertenezcan a un mismo grupo van a tener un comportamiento similar -en términos de representatividad y poder predictivo.
Si Argentina y Chile están en el group_1, entonces son iguales, y así es cómo las verá el modelo.
2.3.10 Representatividad o tamaño de muestra
Este concepto aplica al análisis de cualquier variable categórica, pero es un tema muy común en la ciencia de datos y las estadísticas: tamaño de muestra. ¿Cuántos datos necesitamos para ver el patrón bien desarrollado?
En una variable categórica: ¿Cuántos casos de la categoría “X” necesitamos para confiar en la correlación entre el valor “X” y un valor objetivo? Esto es lo que hemos analizado.
En términos generales: cuanto más difícil sea predecir un evento, más casos vamos a necesitar…
Más adelante en este libro abarcaremos este tema desde otros puntos de vista refiriéndonos de vuelta a esta página.
2.3.11 Reflexiones finales
Vimos dos casos para reducir la cardinalidad, al primero no le importa la variable objetivo, lo que puede ser peligroso en un modelo predictivo, mientras que al segundo sí. Crea una nueva variable basada en la afinidad -y representatividad- de cada categoría de entrada con la variable objetivo.
Concepto clave: representatividad de cada categoría respecto a sí misma, y respecto al evento que se va a predecir. Un buen punto a explorar es analizarlo basándonos en pruebas estadísticas.
Lo que se mencionó al principio con respecto a destruir la información en la variable de entrada implica que la agrupación resultante tiene las mismas proporciones entre grupos (en una variable binaria de entrada).
¿Siempre debemos reducir la cardinalidad? Depende, dos pruebas con un simple dato no son suficientes para extrapolar a todos los casos. Esperamos que sea un buen comienzo para que el lector empiece a hacer sus propias optimizaciones cuando lo considere relevante para el proyecto.
2.3.12 Lecturas adicionales
- El siguiente enlace contiene muchos resultados de precisión diferentes basados en distintos tratamientos para variables categóricas: Beyond One-Hot: an exploration of categorical variables.

2.4 Tratamiento de valores atípicos
2.4.1 ¿De qué se trata esto?
El concepto de valores extremos, al igual que otros temas en machine learning, no es un concepto exclusivo de esta área. Lo que hoy es un valor atípico puede que mañana no lo sea. Los límites entre el comportamiento normal y el anormal son difusos; por otro lado, pararse en los extremos es fácil.

Imagen creada por: Guillermo Mesyngier
¿Qué vamos a repasar en este capítulo?
- ¿Qué es un valor atípico? Enfoques filosóficos y prácticos
- Valores atípicos por dimensionalidad y tipo de datos (numéricos o categóricos)
- Cómo detectar valores atípicos en R (bottom/top X%, Tukey y Hampel)
- Preparación de valores atípicos para análisis numérico en R
- Preparación de valores atípicos para modelado predictivo en R
2.4.2 La intuición detrás de los valores atípicos
Por ejemplo, consideren la siguiente distribución:
# Cargar ggplot2 para visualizar la distribución
library(ggplot2)
# Crear un conjunto de datos de muestra
set.seed(31415)
df_1=data.frame(var=round(10000*rbeta(1000,0.15,2.5)))
# Graficar
ggplot(df_1, aes(var, fill=var)) + geom_histogram(bins=20) + theme_light()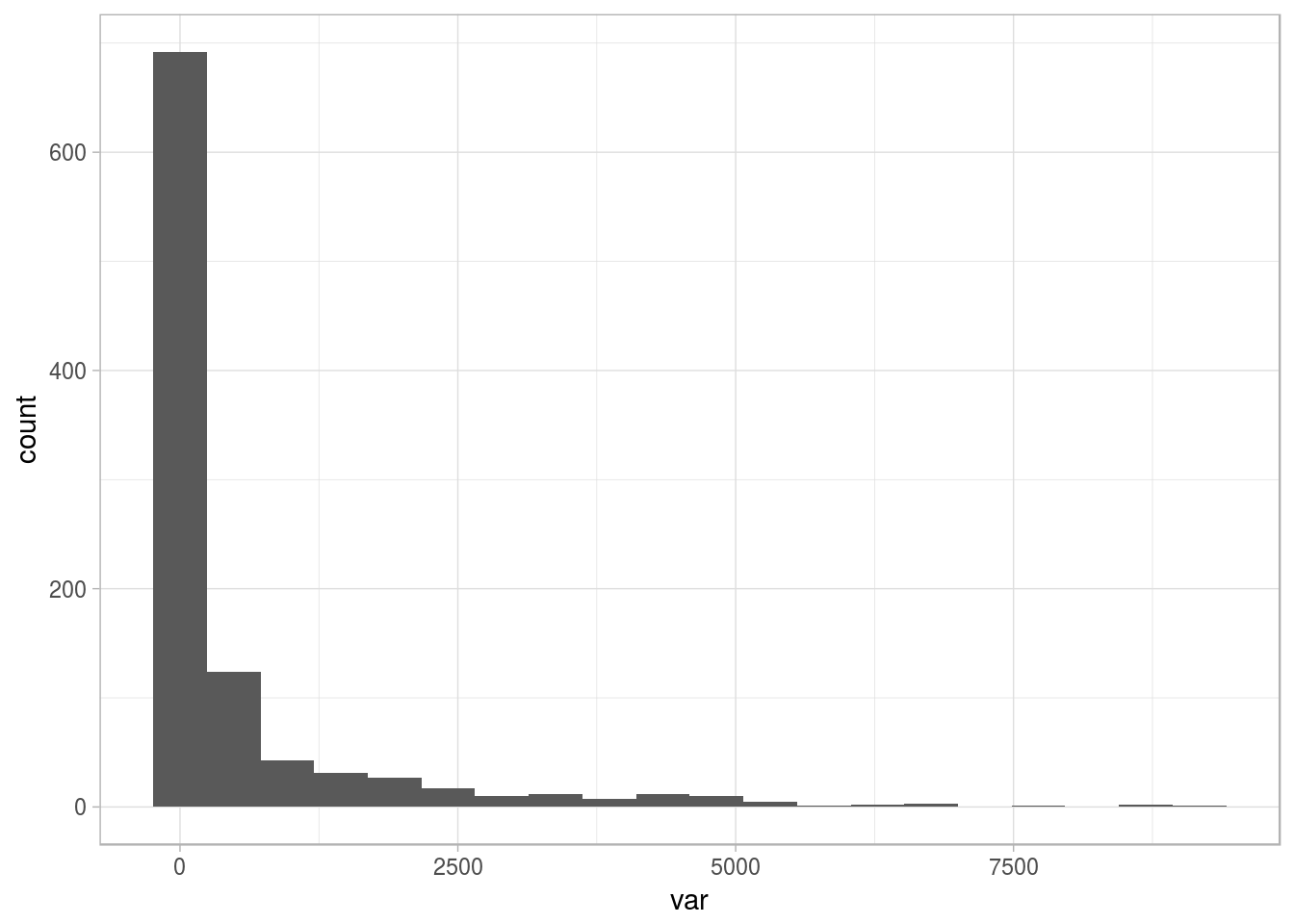
Figure 2.15: Distribución de muestra con cola larga
La variable está sesgada hacia la izquierda, mostrando algunos puntos atípicos a la derecha. Queremos lidiar con ellos. (😎). Entonces, surge la pregunta: ¿Dónde definimos el umbral de lo extremo? Basándonos en la intuición, puede ser el 1% más alto, o podemos analizar cómo cambia el promedio si quitamos el 1% más alto.
Ambos casos podrían estar bien. De hecho, tomar otro número como el umbral (es decir, 2% o 0,1%), también puede ser correcto. Vamos a visualizarlos:
# Calcular los percentiles del 3% y 1% superior
percentile_var=quantile(df_1$var, c(0.98, 0.99, 0.999), na.rm = T)
df_p=data.frame(value=percentile_var, percentile=c("a_98th", "b_99th", "c_99.9th"))
# Graficar la misma distribución más los percentiles
ggplot(df_1, aes(var)) + geom_histogram(bins=20) + geom_vline(data=df_p, aes(xintercept=value, colour = percentile), show.legend = TRUE, linetype="dashed") + theme_light()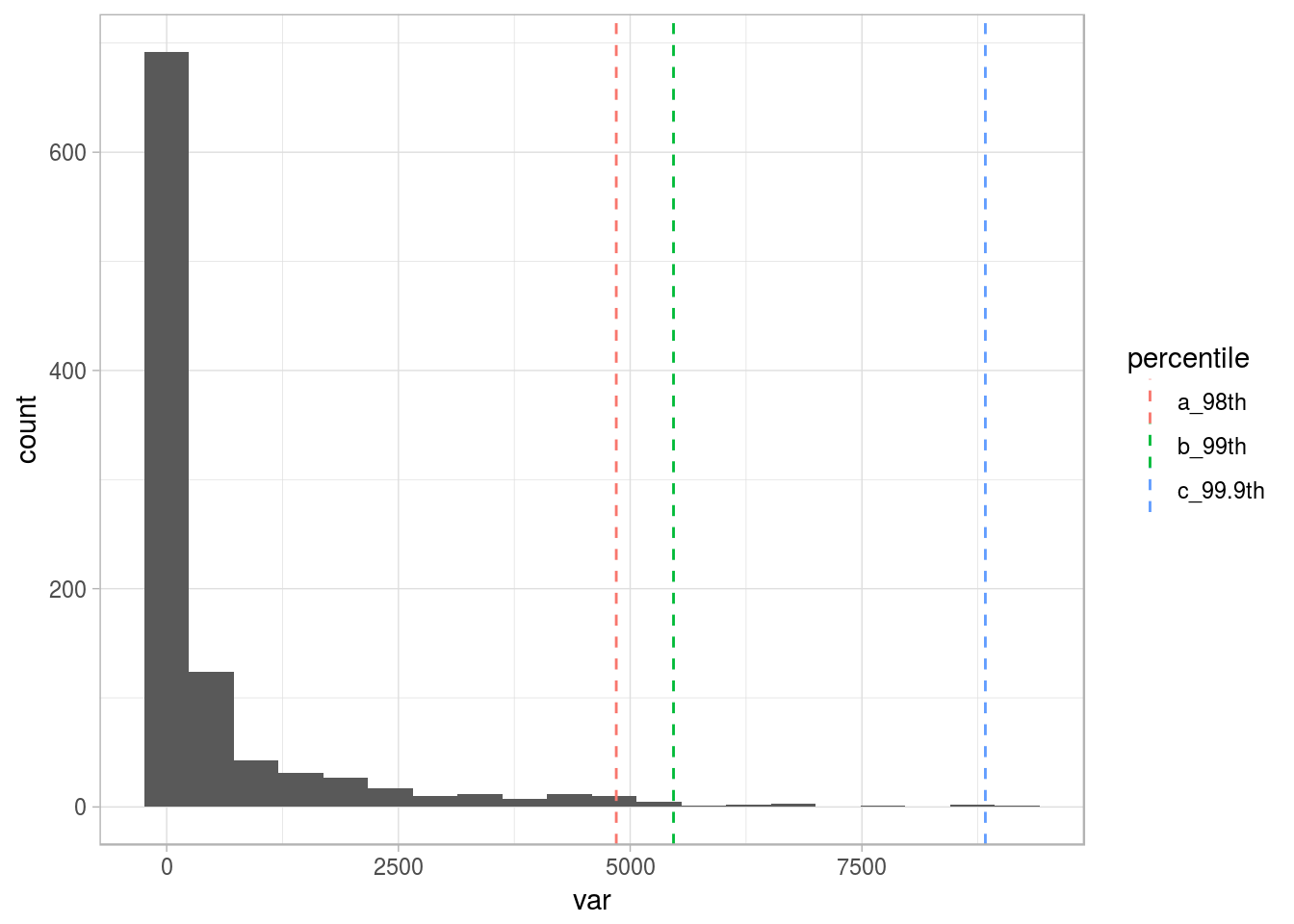
Figure 2.16: Diferentes umbrales para valores atípicos
Para entender los percentiles en mayor profundidad, por favor diríanse al capítulo Anexo 1: La magia de los percentiles.
Por ahora, seguiremos con el 1% superior (percentil 99) como el umbral para marcar todos los puntos que estén más allá como valores atípicos.
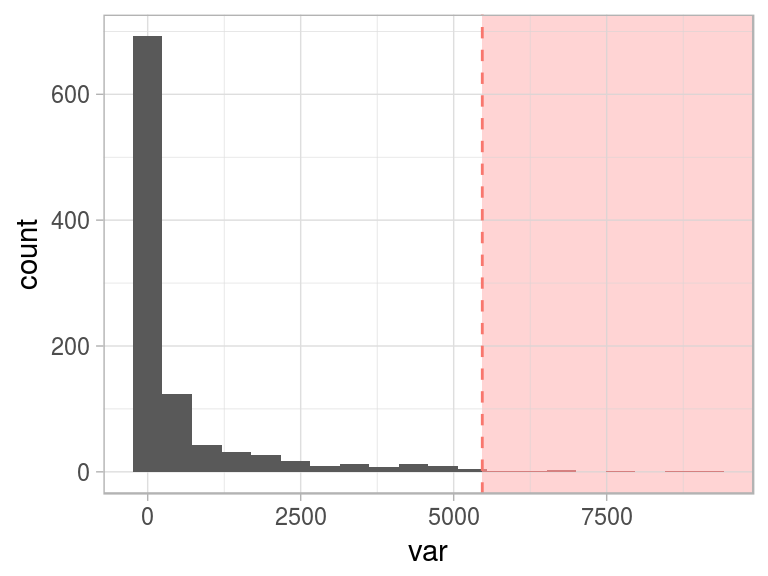
Figure 2.17: Marcando el 1 porciento superior como atípico
Aquí surge un elemento conceptual interesante: cuando definimos lo anormal (o una anomalía), el concepto de normal emerge como su opuesto.
Este comportamiento “normal” está representado en el área verde:
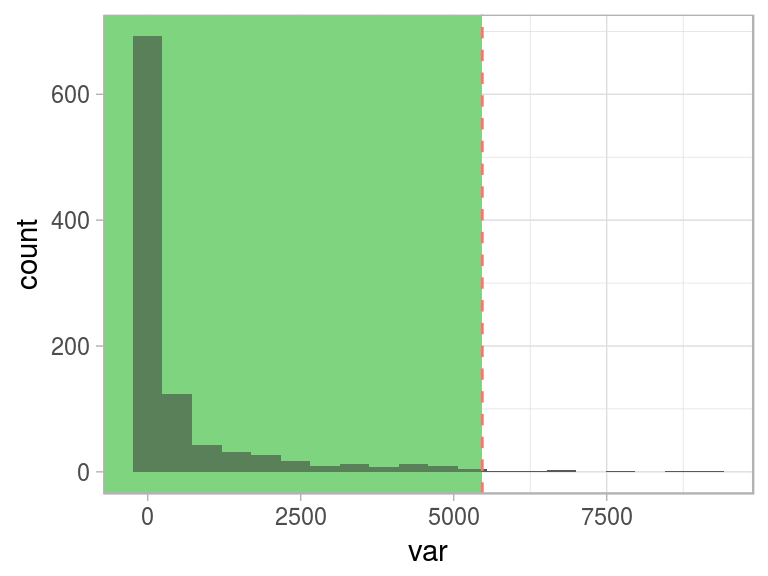
Figure 2.18: Mismo umbral, diferente perspectiva
Lo difícil es determinar dónde se separa lo normal de lo anormal. Hay varios enfoques para lidiar con esto. Vamos a repasar algunos de ellos.
2.4.3 ¿Cuál es el límite entre clima cálido y clima frío?
Hagamos esta sección más filosófica. Algunos buenos matemáticos también fueron filósofos, como es el caso de Pitágoras e Isaac Newton.
¿Dónde podemos poner el umbral para indicar que comienza el clima cálido o, a la inversa, que termina el clima frío?

Figure 2.19: ¿Cuál es el punto de corte?
Cerca del Ecuador, una temperatura cerca de los 10ºC (50ºF) probablemente sea un valor extremadamente bajo; sin embargo, en la Antártida, ¡sería un día de playa! ⛄️ 🏖
👺: “¡Oh! ¡Pero eso sería tomar un ejemplo extremo con dos locaciones diferentes!”
¡No hay problema! Hagamos zoom a una ciudad, como un fractal, el límite donde una empieza (y otra termina) no tendrá un único valor para determinar lo siguiente: “Ok, el clima cálido empieza en los 25.5ºC (78ºF).”
Es relativo.
Sin embargo, es bastante fácil pararse en los extremos, donde la incertidumbre disminuye a casi cero. Por ejemplo, cuando consideramos una temperatura de 60ºC (140ºF).
🤔: “Ok. Pero, ¿cómo se relacionan estos conceptos con machine learning?”
Estamos exponiendo aquí la relatividad que existe al considerar una etiqueta (cálido/frío) como una variable numérica (temperatura). Esto puede ser considerado para cualquier otra variable numérica, como los ingresos económicos y las etiquetas “normal” y “anormal”.
Entender los valores extremos es una de las primeras tareas en análisis exploratorio de datos. Entonces podremos ver cuáles son los valores normales. Esto se trata en el capítulo Análisis numérico, La voz de los números.
Existen varios métodos para marcar valores como valores atípicos. Así como podríamos analizar la temperatura, esta marca es relativa y todos los métodos pueden ser correctos. El método más rápido puede ser tratar el X% superior e inferior como valores atípicos.
Los métodos más robustos consideran las variables de distribución utilizando cuantiles (método de Tukey) o la dispersión de los valores a través de la desviación estándar (método de Hampel).
La definición de estos límites es una de las tareas más comunes en machine learning. ¿Por qué? ¿Cuándo? Señalemos dos ejemplos:
Ejemplo 1: Cuando desarrollamos un modelo predictivo que devuelve una probabilidad de llamar o no llamar a un determinado cliente, necesitamos configurar el umbral para asignar la etiqueta final: “¡sí, llamar!”/“no llamar”. Hay más información sobre esto en el capítulo de Scoring de datos.
Ejemplo 2: Otro ejemplo se da cuando necesitamos discretizar una variable numérica porque necesitamos que sea categórica. Los límites en cada segmento afectarán al resultado general. Hay más información sobre esto en la sección Discretizando variables numéricas
📌 Volviendo al problema original (¿Dónde termina el clima frío?), no todas las preguntas necesitan una respuesta: algunas solamente nos ayudan a pensar.
2.4.4 El impacto de los valores atípicos
2.4.4.1 Construcción de modelos
Algunos modelos, como el bosque aleatorio y las máquinas de potenciación del gradiente, tienden a lidiar mejor con los valores atípicos; sin embargo, el “ruido” puede afectar los resultados de todos modos. El impacto de los valores atípicos en estos modelos es menor que en otros, como las regresiones lineales, las regresiones logísticas, los kmeans y los árboles de decisión.
Un aspecto que contribuye a la disminución del impacto es que ambos modelos crean muchos sub-modelos. Si cualquiera de los modelos toma un valor atípico como información, entonces otros sub-modelos probablemente no lo harán; por lo tanto, el error se cancela. El equilibrio yace en la pluralidad de voces.
2.4.4.2 Comunicar los resultados 🌍 📣
Si debemos informar cuáles fueron las variables utilizadas en el modelo, terminaremos quitando los valores atípicos para no mostrar un histograma con una sola barra y/o un sesgo en el promedio.
Es mejor mostrar un número no sesgado que justificar que el modelo podrá lidiar con valores extremos.
2.4.4.3 Tipos de valores atípicos según el tipo de datos
- Numéricos 📏: como los que vimos antes:
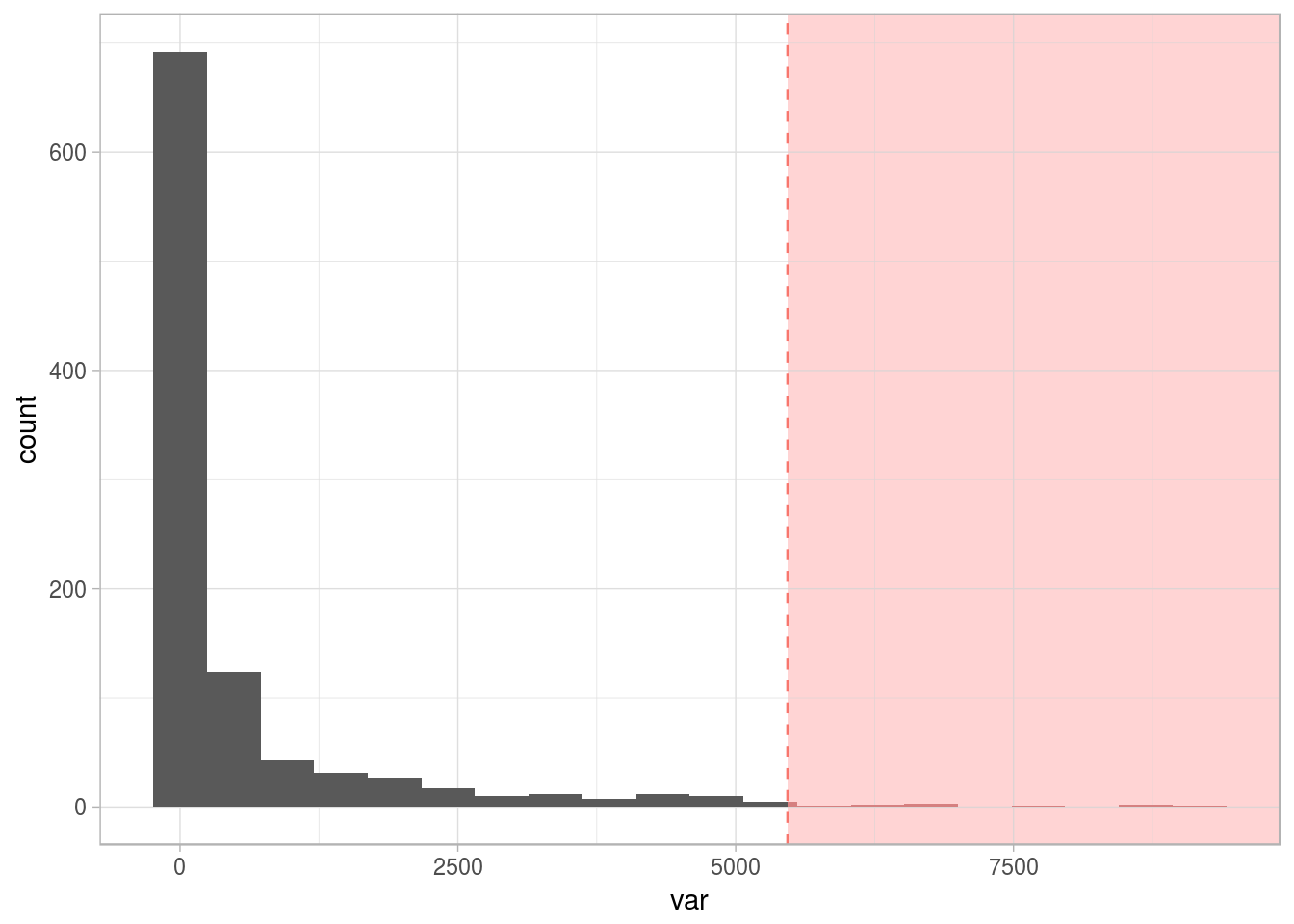
Figure 2.20: Variable numérica con valores atípicos
- Categóricos 📊: Tener una variable en la que la dispersión de la categorías es bastante alta (alta cardinalidad): por ejemplo, código postal. Hay más información sobre cómo lidiar con valores atípicos en variables categóricas en el capítulo Variables de alta cardinalidad en estadística descriptiva.
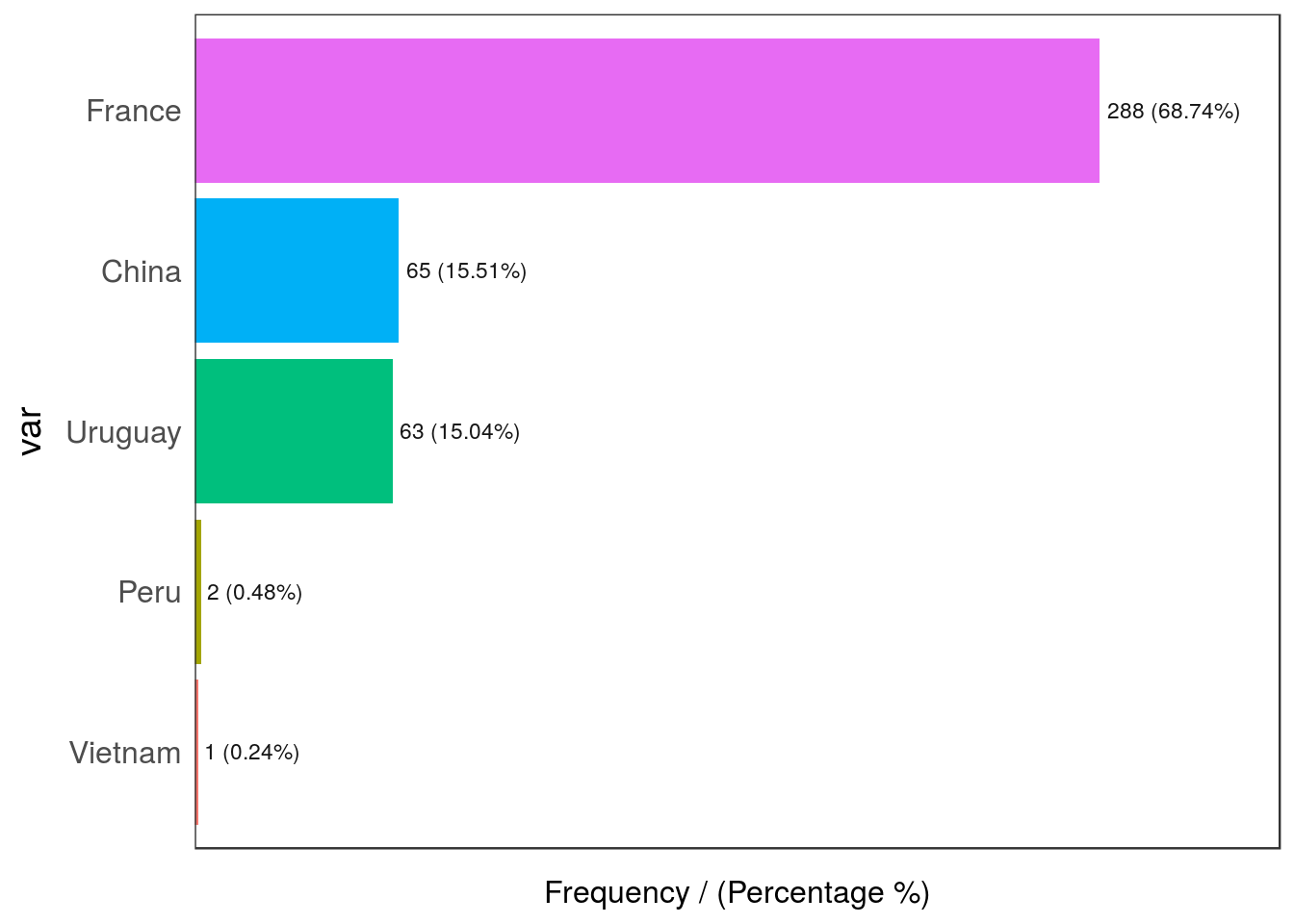
Figure 2.21: Variable categórica con valores atípicos
## var frequency percentage cumulative_perc
## 1 France 288 68.74 68.74
## 2 China 65 15.51 84.25
## 3 Uruguay 63 15.04 99.29
## 4 Peru 2 0.48 99.77
## 5 Vietnam 1 0.24 100.00Peru y Vietnam son valores atípicos en este ejemplo dado que su participación en los datos es inferior al 1%.
2.4.4.4 Tipos de valores atípicos según dimensionalidad
Hasta ahora, hemos observado valores atípicos unidimensionales y univariados. También podemos considerar dos o más variables en simultáneo.
Por ejemplo, tenemos el siguiente conjunto de datos, df_hello_world, con dos variables: v1 y v2. Haciendo el mismo análisis que antes:
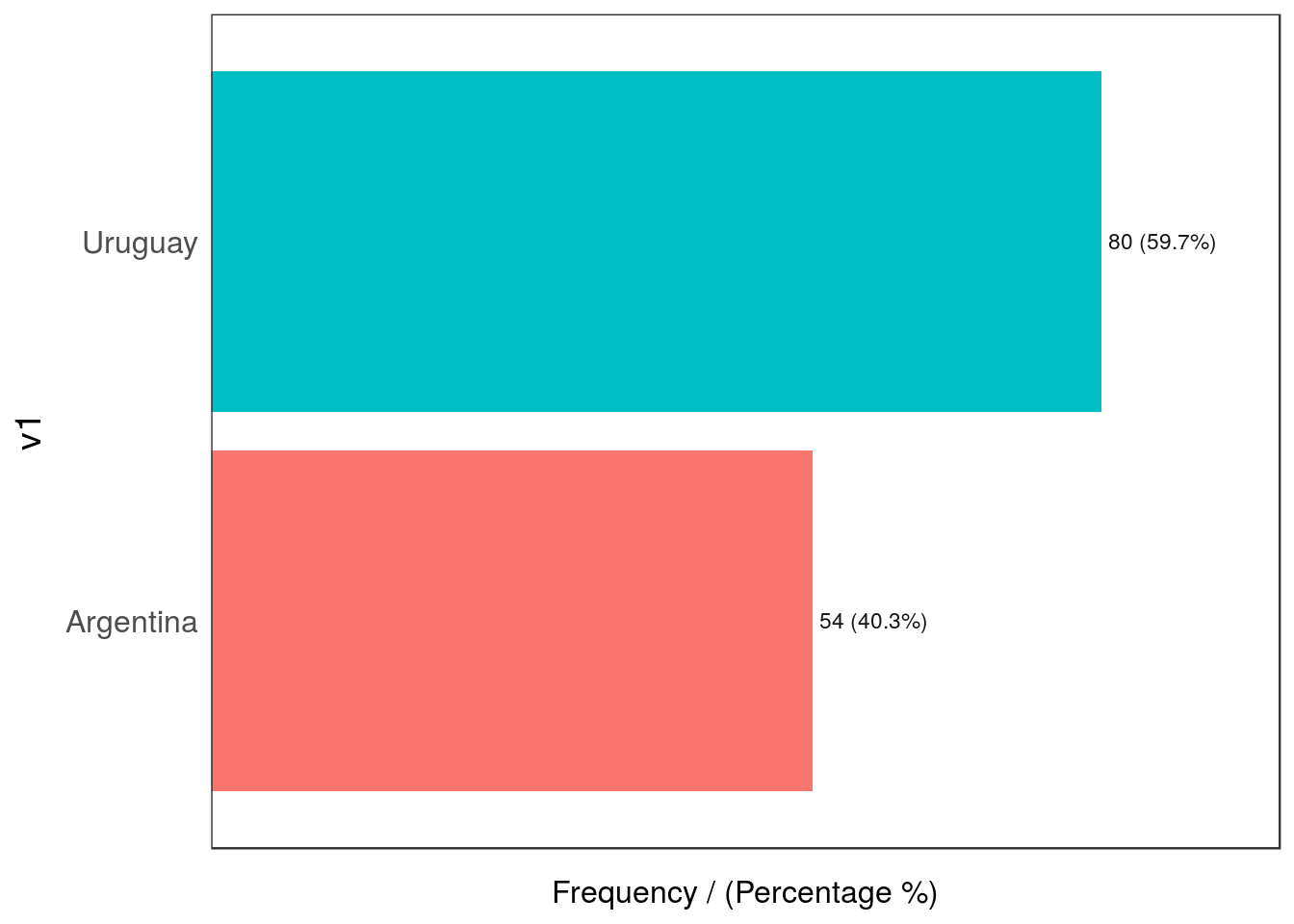
Figure 2.22: Valores atípicos según dimensionalidad
## v1 frequency percentage cumulative_perc
## 1 Uruguay 80 59.7 59.7
## 2 Argentina 54 40.3 100.0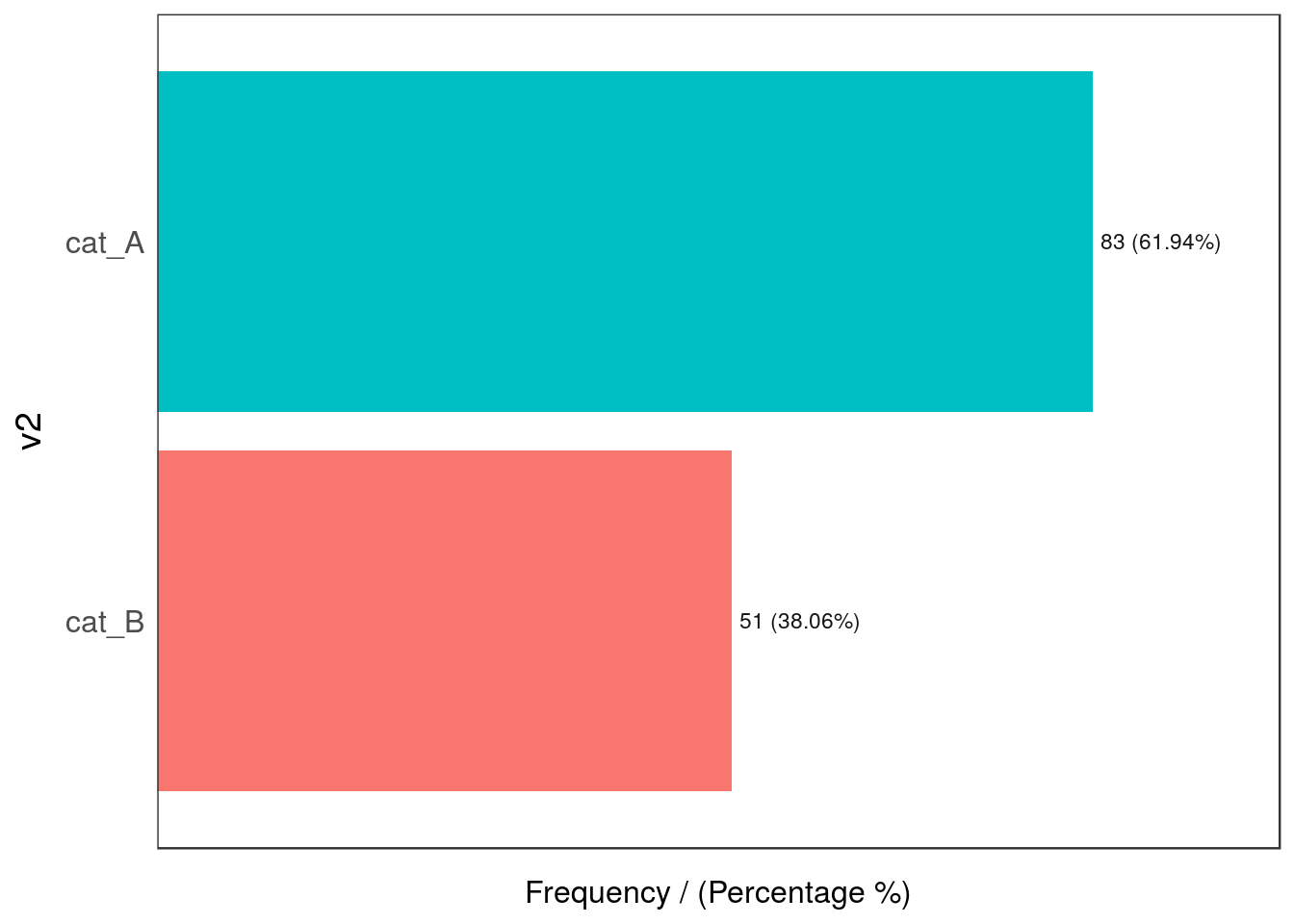
Figure 2.22: Valores atípicos según dimensionalidad
## v2 frequency percentage cumulative_perc
## 1 cat_A 83 61.94 61.94
## 2 cat_B 51 38.06 100.00## [1] "Variables processed: v1, v2"Por ahora no hay valores atípicos, ¿correcto?
Ahora creamos una tabla de contingencia que nos diga la distribución de ambas variables, una contra la otra:
## v2
## v1 cat_A cat_B
## Argentina 39.55 0.75
## Uruguay 22.39 37.31¡Oh 😱! La combinación de Argentina y cat_B es realmente baja (0.75%) en comparación con los otros valores (menos del 1%), mientras que las otras intersecciones están por encima del 22%.
2.4.4.5 Algunas reflexiones…
Los últimos ejemplos muestran el potencial de los valores extremos o atípicos y están presentados como consideraciones que tenemos que tener en cuenta con un nuevo conjunto de datos.
Mencionamos 1% como un posible umbral para marcar un valor como atípico. Este número podría ser 0.5% o 3%, dependiendo del caso.
Además, la presencia de este tipo de valores atípicos podría no traer problemas.
2.4.5 Cómo lidiar con valores atípicos en R
La función prep_outliers que viene incluida en el paquete funModeling puede ayudarnos con esta tarea. Puede manejar de una a ‘N’ variables en simultáneo (especificando el parámetro input).
El núcleo es el siguiente:
- Soporta tres métodos diferentes (parámetro
method) para considerar un valor como un outlier: bottom_top, Tukey, y Hampel. - Funciona en dos modos (parámetro
type) al establecer un valorNAo al frenar la variable en un valor particular. - Además de la explicación a continuación,
prep_outlierses una función bien documentada:help("prep_outliers").
2.4.6 Paso 1: Cómo detectar valores atípicos 🔎
Los siguientes métodos se implementan en la función prep_outliers. Obtienen diferentes resultados para que el usuario pueda seleccionar los que mejor se ajustan a sus necesidades.
2.4.6.0.1 Método de valores ‘bottom’ y ‘top’
Esto considera valores atípicos tomando los valores del X% inferior y superior, basados en el percentil. Los puntos de corte más utilizados son 0.5%, 1%, 1.5%, 3%, entre otros.
Configurando el parámetro top_percent en 0.01 se tratarán todos los valores del 1% superior.
La misma lógica aplica a los valores más bajos: si se establece el parámetro bottom_percent en 0.01 se marcará como valores atípicos al 1% más bajo de todos los valores.
La función interna utilizada es quantile; si queremos marcar el 1% inferior y el superior, escribimos:
quantile(heart_disease$age, probs = c(0.01, 0.99), na.rm = T)## 1% 99%
## 35 71Todos los valores para aquellos casos que tengan menos de 35 años o más de 71 serán considerados atípicos.
Para leer más sobre percentiles, diríjanse al capítulo: Anexo 1: La magia de los percentiles.
2.4.6.0.2 Método de Tukey
Este método marca valores atípicos utilizando los valores cuartiles, Q1, Q2, y Q3, donde Q1 es esquivalente al percentil 25, Q2 al percentil 50 (también conocido como la mediana), y Q3 es el percentil 75.
El rango intercuartil (IQR por sus siglas en inglés) se calcula haciendo Q3 - Q1.
La fórmula:
- El umbral inferior es: Q1 - 3*IQR. Todos los valores que queden por debajo son considerados atípicos.
- El umbral superior es: Q1 + 3*IQR. Todos los valores que queden por encima son considerados atípicos.
El valor 3 es para detectar el límite “extremo”. Este método viene del diagrama de caja, donde el multiplicador es 1.5 (no 3). Esto hace que muchos más valores sean marcados como atípicos, lo veremos en la siguiente imagen.
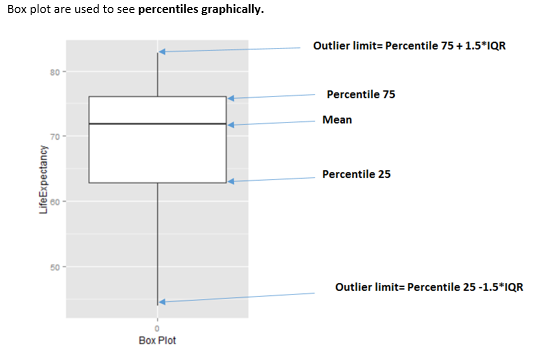
Figure 2.23: Cómo interpretar un diagrama de caja
Podemos acceder a la función interna utilizada en prep_outliers para calcular el límite de Tukey:
tukey_outlier(heart_disease$age)## bottom_threshold top_threshold
## 9 100Devuelve un vector de dos valores; por lo tanto, tenemos el umbral inferior y el superior: todos los valores que estén por debajo de nueve y por encima de 100 serán considerados atípicos.
Encontrarán un ejemplo visual, simple y paso a paso en [tukey_outliers].
2.4.6.0.3 Método de Hampel
La fórmula:
- El umbral inferior es:
median_value - 3*mad_value. Todos los valores que queden por debajo son considerados atípicos. - El umbral superior es:
median_value + 3*mad_value. Todos los valores que queden por encima son considerados atípicos.
Podemos acceder a la función interna utilizada en prep_outliers para calcular el límite de Hampel:
hampel_outlier(heart_disease$age)## bottom_threshold top_threshold
## 29.3132 82.6868Devuelve un vector de dos valores; por lo tanto, tenemos el umbral inferior y el superior: todos los valores que estén por debajo de 29.31 y por encima de 82.68 serán considerados atípicos.
Tiene un parámetro llamado k_mad_value, y su valor por defecto es 3. El valor k_mad_value puede ser modificado, pero no en la función prep_outliers por ahora.
Cuanto más alto sea el valor k_mad_value, más altos serán los límites de los umbrales.
hampel_outlier(heart_disease$age, k_mad_value = 6) ## bottom_threshold top_threshold
## 2.6264 109.37362.4.7 Paso 2: ¿Qué hacemos con los valores atípicos? 🛠
Ya detectamos qué puntos son los atípicos. Ahora, la pregunta es ¿Qué hacemos con ellos? 🤔
Hay dos escenarios posibles:
- Escenario 1: Preparar los valores atípicos para el análisis numérico
- Escenario 2: Preparar los valores atípicos para modelado predictivo
Hay un tercer escenario en el que no hacemos nada con los valores atípicos detectados. Simplemente los dejamos ser.
Proponemos recurrir a la función prep_outliers del paquete funModeling que nos dará una mano con esta tarea.
Más allá de la función en sí, lo importante aquí es el concepto subyacente y la posibilidad de desarrollar un método superador.
La función prep_outliers abarca estos dos escenarios con el parámetro type:
type = "set_na", para el escenario 1type = "stop", para el escenario 2
2.4.7.1 Escenario 1: Preparar los valores atípicos para el análisis numérico
El análisis inicial:
En este caso, todos los valores atípicos son convertidos a NA, por lo que, al aplicar la mayoría de las funciones características (máx, mín, promedio, etc.) obtendremos un valor menos sesgado. Recuerden configurar el parámetro na.rm=TRUE en dichas funciones. De lo contrario, el resultado será NA.
Por ejemplo, consideremos la siguiente variable (la que vimos al principio con algunos valores atípicos):
# Para entender todas estas métricas, por favor diríjanse al capítulo sobre Análisis numérico
profiling_num(df_1$var)## variable mean std_dev variation_coef p_01 p_05 p_25 p_50 p_75 p_95 p_99
## 1 var 548 1226 2.2 0 0 0 24 370 3382 5467
## skewness kurtosis iqr range_98 range_80
## 1 3.3 16 370 [0, 5467.33] [0, 1791.1]Aquí podemos ver varios indicadores que nos dan algunas pistas. El desvío estándar std_dev es realmente alto comparado con el promedio mean, y eso se refleja en el coeficiente de variación variation_coef. Además, la curtosis es alta (16) y el valor de p_99 es casi el doble que el de p_95 (5767 vs. 3382).
Esta última tarea de mirar algunos números y visualizar la distribución de la variable es como imaginar una fotografía por lo que otra persona nos dice: convertimos la voz (que es una señal) en una imagen en nuestro cerebro. 🗣 🙄 … => 🏔
2.4.7.1.1 Utilizar prep_outliers para el análisis numérico
Debemos configurar type="set_na". Esto implica que cada punto marcado como un valor atípico será convertido a NA.
Usaremos los tres métodos: Tukey, Hampel, y bottom/top X%.
Usando el método de Tukey:
df_1$var_tukey=prep_outliers(df_1$var, type = "set_na", method = "tukey")Ahora verificamos cuántos valores NA había antes (la variable original) y después de la transformación basada en Tukey.
# Antes
df_status(df_1$var, print_results = F) %>% select(variable, q_na, p_na)## variable q_na p_na
## 1 var 0 0# Después
df_status(df_1$var_tukey, print_results = F) %>% select(variable, q_na, p_na)## variable q_na p_na
## 1 var 120 12Antes de la transformación, había 0 valores NA, mientras que después 120 valores (cerca del 12%) fueron marcados como atípicos de acuerdo a la prueba de Tukey y reemplazados por NA.
Podemos comparar el antes y el después:
profiling_num(df_1, print_results = F) %>% select(variable, mean, std_dev, variation_coef, kurtosis, range_98)## variable mean std_dev variation_coef kurtosis range_98
## 1 var 548 1226 2.2 15.6 [0, 5467.33]
## 2 var_tukey 163 307 1.9 8.4 [0, 1358.46]El promedio disminuyó casi en una tercera parte, y todas las demás métricas también disminuyeron.
Método de Hampel:
Veamos qué pasa con el método de Hampel (method="hampel"):
df_1$var_hampel=prep_outliers(df_1$var, type = "set_na", method="hampel")Verificando…
df_status(df_1, print_results = F) %>% select(variable, q_na, p_na)## variable q_na p_na
## 1 var 0 0
## 2 var_tukey 120 12
## 3 var_hampel 364 36Este último método es mucho más severo al identificar valores atípicos, marcando el 36% de los valores como atípicos. Es probable que esto se deba a que la variable está bastante sesgada hacia la izquierda.
Método del ‘bottom’ y ‘top’ X%
Por último, podemos probar el método más fácil: quitar el 2% superior.
df_1$var_top2=prep_outliers(df_1$var, type = "set_na", method="bottom_top", top_percent = 0.02)Por favor noten que el valor de 2% fue asignado arbitrariamente. También pueden intentar con otros valores, como 3% o 0.5%.
¡Es ahora de comparar todos los métodos!
2.4.7.1.2 Uniendo todo lo que vimos
Tomaremos algunos indicadores para realizar la comparación cuantitativa.
df_status(df_1, print_results = F) %>% select(variable, q_na, p_na)## variable q_na p_na
## 1 var 0 0
## 2 var_tukey 120 12
## 3 var_hampel 364 36
## 4 var_top2 20 2prof_num=profiling_num(df_1, print_results = F) %>% select(variable, mean, std_dev, variation_coef, kurtosis, range_98)
prof_num## variable mean std_dev variation_coef kurtosis range_98
## 1 var 548 1226 2.2 15.6 [0, 5467.33]
## 2 var_tukey 163 307 1.9 8.4 [0, 1358.46]
## 3 var_hampel 17 31 1.8 6.0 [0, 118.3]
## 4 var_top2 432 908 2.1 10.9 [0, 4364.29]Graficar
# Primero debemos convertir el conjunto de datos a formato ancho
df_1_m=reshape2::melt(df_1)
plotar(df_1_m, target= "variable", input = "value", plot_type = "boxplot")
Figure 2.24: Comparación de métodos para identificar valores atípicos
Al seleccionar el bottom/top X%, siempre tendremos algunos valores que cumplan con esa condición, mientras que en los otros dos métodos puede que esto no suceda.
2.4.7.1.3 Conclusiones sobre el manejo de valores atípicos en el análisis numérico
La idea es modificar los valores atípicos lo menos posible (por ejemplo, si estamos interesados solamente en describir el comportamiento general).
Para lograr eso -a la hora de crear un informe ad hoc, por ejemplo- podemos usar el promedio. Podríamos elegir el método del 2% superior porque solo afecta al 2% de todos los valores y provoca una disminución drástica en el promedio: de 548 a 432, o 21% menos.
“Modificar o no modificar el conjunto de datos, esa es la cuestión.” William Shakespeare como científico de datos.
El método de Hampel modificó demasiado el promedio, ¡de 584 a 17! Eso fue tomando el valor estándar de este método, que es 3-MAD (un desvío estándar un tanto robusto).
Por favor tengan en cuenta que esta demostración no significa que Hampel o Tukey sean una mala elección. De hecho, son métodos más robustos porque el umbral puede ser más alto que el valor actual; de hecho, ningun valor es tratado como atípico.
En el otro extremo, podemos considerar, por ejemplo, la variable age de los datos heart_disease. Analicemos sus valores atípicos:
# Obtener el umbral de valores atípicos
tukey_outlier(heart_disease$age)## bottom_threshold top_threshold
## 9 100# Obtener los valores mínimos y máximos
min(heart_disease$age)## [1] 29max(heart_disease$age)## [1] 77- El umbral inferior es 9, y el valor mínimo es 29.
- El umbral superior es 100, y el valor máximo es 77.
Ergo: la variable age no tiene valores atípicos.
Si hubiéramos utilizado el método bottom/top X%, entonces los datos dentro de esos porcentajes hubieran sido detectados como valores atípicos.
Todos los ejemplos que vimos hasta ahora tomaron una sola variable a la vez; no obstante, prep_outliers puede manejar varias en simultáneo usando el parámetro input como veremos en la siguiente sección. Todo lo que vimos hasta aquí será equivalente, excepto lo que hacemos una vez que detectamos los valores atípicos, es decir, el método de imputación.
2.4.7.2 Escenario 2: Preparar los valores atípicos para modelado predictivo
El caso anterior da como resultado que los valores atípicos observados se convierten a valores NA. Esto es un gran problema si estamos construyendo un modelo de machine learning, ya que muchos de ellos no funcionan con valores NA. Hay más información sobre el manejo de datos faltantes en el capítulo Datos faltantes.
Para lidiar con valores atípicos y poder usar un modelo predictivo, una buena idea es configurar el parámetro type='stop', para que todos los valores marcados como atípicos sean convertidos al valor del umbral.
Algunas cosas a tener en cuenta:
Traten de pensar en el tratamiento (y creación) de las variables como si se lo estuvieran explicando al modelo. Al frenar las variables en un determinado valor, 1% por ejemplo, le estamos diciendo al modelo: Hey, modelo, por favor considera todos los valores extremos como si estuvieran en el percentil 99, dado que este valor ya es lo suficientemente alto. Gracias.
Algunos modelos predictivos son más tolerantes al ruido que otros. Podemos ayudarlos tratando algunos de los valores atípicos. En la práctica, pre-procesar datos tratando los atípicos tiende a producir resultados más precisos cuando estamos en presencia de datos nunca vistos.
2.4.7.3 Imputar valores atípicos para modelado predictivo
Primero, creamos un conjunto de datos con algunos valores atípicos. Ahora el ejemplo tiene dos variables.
# Crear data frame con valores atípicos
# Desactivar la notación científica
options(scipen=999)
# Configurar seed para que tenga un ejemplo reproducible
set.seed(10)
# Crear las variables
df_2=data.frame(var1=rchisq(1000,df = 1), var2=rnorm(1000))
# Forzar los valores atípicos
df_2=rbind(df_2, 135, rep(400, 30), 245, 300, 303, 200) Lidiar con los valores atípicos en ambas variables (var1 y var2) usando el método de Tukey:
df_2_tukey=prep_outliers(data = df_2, input = c("var1", "var2"), type='stop', method = "tukey")Verificar algunas métricas antes y después de la imputación:
profiling_num(df_2, print_results = F) %>% select(variable, mean, std_dev, variation_coef)## variable mean std_dev variation_coef
## 1 var1 2.6 21 8.3
## 2 var2 1.6 21 13.6profiling_num(df_2_tukey, print_results = F) %>% select(variable, mean, std_dev, variation_coef)## variable mean std_dev variation_coef
## 1 var1 0.997 1.3 1.3
## 2 var2 0.018 1.0 57.5Tukey funcionó perfectamente esta vez, exponiendo un promedio más preciso para ambas variables: 1 para var1 y 0 para var2.
Observen que esta vez no hay ni un valor NA. Lo que hizo la función esta vez fue frenar la variable en los valores umbral. Ahora, los valores mínimos y máximos serán los mismos que informó el método de Tukey.
Verificar el umbral para var1:
tukey_outlier(df_2$var1)## bottom_threshold top_threshold
## -3.8 5.3Ahora verificamos los valores min/max antes de la transformación:
# Antes:
min(df_2$var1)## [1] 0.0000031max(df_2$var1)## [1] 400y después de la transformación…
# Después
min(df_2_tukey$var1)## [1] 0.0000031max(df_2_tukey$var1)## [1] 5.3El mínimo sigue siendo el mismo (0.0000031), pero el máximo fue ajustado al valor de Tukey de ~5.3.
Los cinco valores más altos antes de la pre-partición eran:
# Antes
tail(df_2$var1[order(df_2$var1)], 5)## [1] 200 245 300 303 400pero después…
# Después:
tail(df_2_tukey$var1[order(df_2_tukey$var1)], 5)## [1] 5.3 5.3 5.3 5.3 5.3Y verificamos que no haya ningún NA:
df_status(df_2_tukey, print_results = F) %>% select(variable, q_na, p_na)## variable q_na p_na
## 1 var1 0 0
## 2 var2 0 0Bastante claro, ¿no?
Ahora repliquemos el ejemplo que vimos en la última sección con una sola variable para comparar los tres métodos.
df_2$tukey_var2=prep_outliers(data=df_2$var2, type='stop', method = "tukey")
df_2$hampel_var2=prep_outliers(data=df_2$var2, type='stop', method = "hampel")
df_2$bot_top_var2=prep_outliers(data=df_2$var2, type='stop', method = "bottom_top", bottom_percent=0.01, top_percent = 0.01)2.4.7.3.1 Uniendo todo lo que vimos
# Excluir var1
df_2_b=select(df_2, -var1)
# Análisis numérico
profiling_num(df_2_b, print_results = F) %>% select(variable, mean, std_dev, variation_coef, kurtosis, range_98)## variable mean std_dev variation_coef kurtosis range_98
## 1 var2 1.5649 21.36 14 223.8 [-2.32, 2.4]
## 2 tukey_var2 0.0178 1.02 58 4.6 [-2.32, 2.4]
## 3 hampel_var2 0.0083 0.98 118 3.2 [-2.32, 2.4]
## 4 bot_top_var2 0.0083 0.97 116 2.9 [-2.32, 2.4]Los tres métodos muestran resultados muy similares con estos datos.
Graficar
# Primero debemos convertir el conjunto de datos a formato ancho
df_2_m=reshape2::melt(df_2_b) %>% filter(value<100)
plotar(df_2_m, target= "variable", input = "value", plot_type = "boxplot")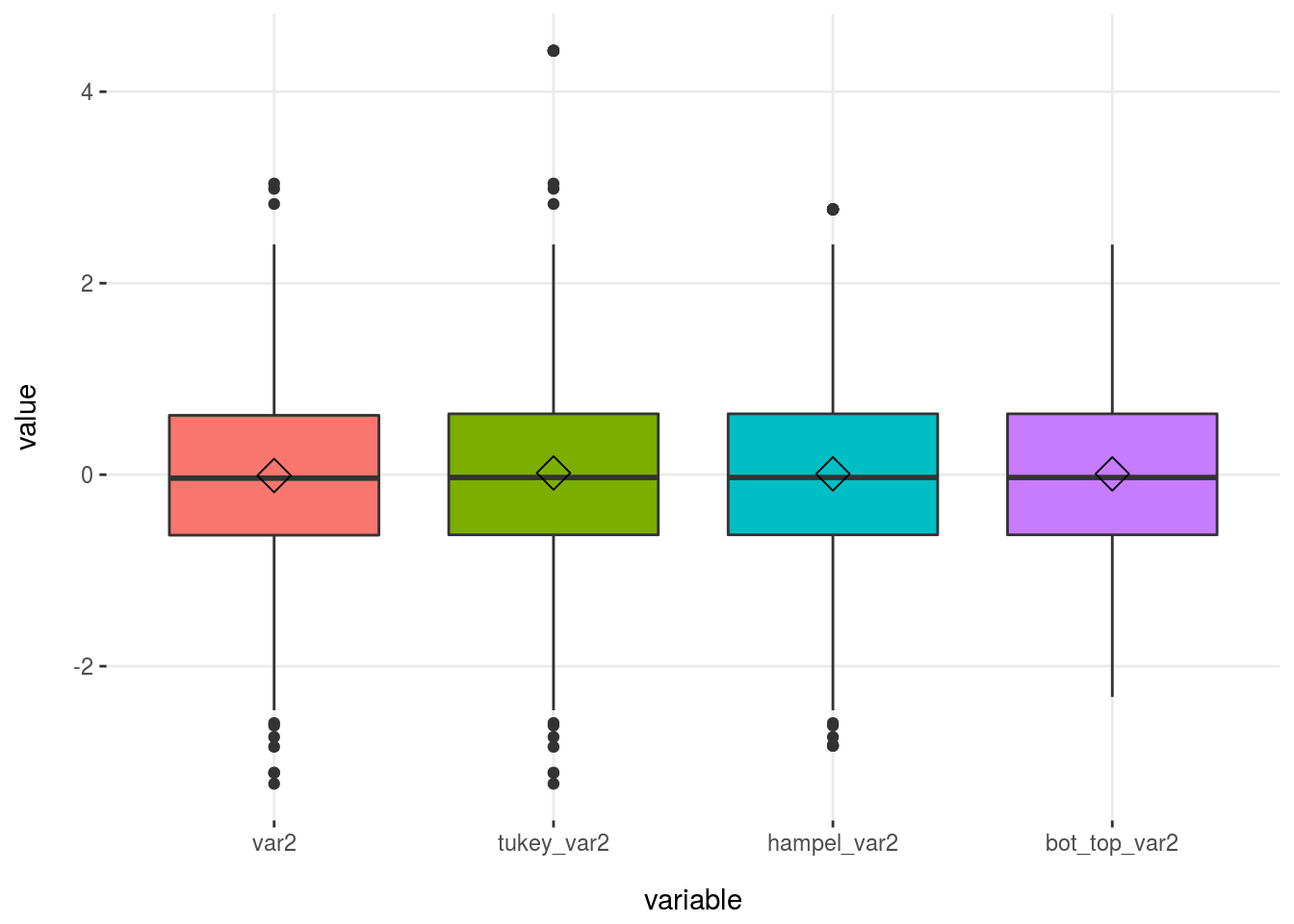
Figure 2.25: Comparación de métodos para identificar valores atípicos
Importante: Los dos puntos que están por encima del valor 100 (sólo para var1) fueron excluidos, de lo contrario, hubiera sido imposible notar la diferencia entre los métodos.
2.4.8 Reflexiones finales
Hemos abordado el tema de los valores atípicos tanto desde una perspectiva filosófica como técnica, invitando al lector a mejorar sus habilidades de pensamiento crítico a la hora de definir los límites (umbrales). Es fácil pararse en los extremos, pero encontrar el equilibrio es una tarea difícil.
En términos técnicos, cubrimos tres métodos con diferentes bases para identificar valores atípicos:
- Bottom/Top X%: Este método siempre marcará valores como atípicos dado que en todas las variables hay un X% inferior y superior.
- Tukey: Se basa en el clásico boxplot, que usa cuartiles.
- Hampel: Es bastante restrictivo si no modificamos el parámetro por defecto. Se basa en la mediana y el valor del MAD (similar al desvío estándar pero menos sensible a los valores atípicos).
Una vez que identificamos los valores atípicos, el siguiente paso es decidir qué hacer con ellos. En algunos casos no es necesario hacer ningún tratamiento. En conjuntos de datos muy pequeños, podemos identificarlos a simple vista.
La regla de: “Sólo modificar lo que es necesario” (que también puede aplicar a la relación entre el ser humano y la naturaleza), nos dice que no tratemos o excluyamos ciegamente todos los valores atípicos extremos. Con cada acción que hicimos, introducimos algún sesgo. Por eso es tan importante saber cuáles son las implicaciones de cada método. Si es una buena decisión o no depende de la naturaleza de los datos que estamos analizando.
En modelado predictivo, aquellos que tienen algún tipo de técnica de remuestreo interno, o crean varios modelos pequeños para llegar a una predicción final, son más estables con los valores extremos. Hay más información sobre remuestreo y error en el capítulo Conociendo el error.
En algunos casos, cuando el modelo predictivo está ejecutándose en producción, es recomendable reportar o considerar la preparación de cualquier valor extremo nuevo, es decir, un valor que no estaba presente durante la construcción del modelo. Hay más información sobre este tema, pero con una variable categórica, en Variables de alta cardinalidad en modelado predictivo, sección: Manejo de nuevas categorías cuando el modelo predictivo está en producción.
Una buena prueba para que haga el lector es tomar un conjunto de datos, tratar los valores atípicos, y luego comparar algunas métricas de desempeño como Kappa, ROC, Precisión (Accuracy), etc.; ¿La preparación de los datos mejoró alguna de ellas? O, en los reportes, ver cuánto cambia el promedio. Incluso graficando, ¿ahora el gráfico nos dice algo? De esta manera, el lector creará nuevo conocimiento basándose en su experiencia.😉.

2.5 Datos faltantes: Análisis, manejo e imputación
2.5.1 ¿De qué se trata esto?
El análisis de los valores faltantes es la estimación del vacío mismo. Los valores faltantes presentan un obstáculo a la hora de crear modelos predictivos, análisis de clusters, reportes, etc.
En este capítulo, ahondaremos en el concepto y tratamiento de valores nulos. Realizaremos análisis utilizando diferentes enfoques e interpretaremos los distintos resultados.
Si todo sale bien, después de estudiar el capítulo entero, el lector podrá entender conceptos clave del manejo de valores faltantes y podrá tomar mejores abordajes que los que proponemos aquí.
¿Qué vamos a repasar en este capítulo?
- ¿Qué es un valor nulo, conceptualmente?
- Cuándo excluir filas o columnas.
- Análisis numérico de valores faltantes.
- Transformación e imputación de variables numéricas y categóricas.
- Imputar valores: desde enfoques simples a algunos más complejos.
Ejemplificaremos estos temas con un enfoque práctico en R. Este código busca ser lo suficientemente genérico para que lo puedan aplicar en sus proyectos 🙂.
2.5.2 Cuando el valor nulo representa información
Los valores vacíos también aparecen como “NULL” en bases de datos, NA en R, o simplemente el string “empty” en programas de hojas de cálculo. También pueden estar representados con algún número, como: 0, -1 o -999.
Por ejemplo, imaginen una agencia de viajes que une dos tablas, una de personas y otra de países. El resultado muestra la cantidad de viajes por persona:
## person South_Africa Brazil Costa_Rica
## 1 Fotero 1 5 5
## 2 Herno NA NA NA
## 3 Mamarul 34 40 NAEn este resultado, Mamarul viajó a South Africa 34 veces.
¿Qué representa el valor NA (o NULL)?
En este caso, NA debería ser reemplazado por 0, indicando cero viajes en esa intersección persona-país. Después de la conversación, la tabla está lista para usar.
Ejemplo: Reemplazar todos los valores NA por 0
# Hacer una copia
df_travel_2=df_travel
# Reemplazar todos los valores NA con 0
df_travel_2[is.na(df_travel_2)]=0
df_travel_2## person South_Africa Brazil Costa_Rica
## 1 Fotero 1 5 5
## 2 Herno 0 0 0
## 3 Mamarul 34 40 0El último ejemplo transforma todos los valores NA en 0. No obstante, en otros escenarios, esta transformación podría no aplicar para todas las columnas.
Ejemplo: Reemplazar los valores NA por 0 sólo en ciertas columnas
Probablemente el escenario más común sea reemplazar NA por algún valor -cero en este caso- sólo en algunas columnas. Definimos un vector que contiene todas las variables a reemplazar y luego aplicamos la función mutate_at del paquete dplyr.
library(dplyr) # vers 0.7.1
# Reemplazar valores NA con 0 solo en las columnas seleccionadas
vars_to_replace=c("Brazil", "Costa_Rica")
df_travel_3=df_travel %>% mutate_at(.vars=vars_to_replace, .funs = funs(ifelse(is.na(.), 0, .)))
df_travel_3## person South_Africa Brazil Costa_Rica
## 1 Fotero 1 5 5
## 2 Herno NA 0 0
## 3 Mamarul 34 40 0Tengan a mano la última función ya que es muy común enfrentarnos a la situación de aplicar una función especificada a un subconjunto de variables y volver a incorporar las variables transformadas y no transformadas al mismo conjunto de datos.
Vamos a un ejemplo más complejo.
2.5.3 Cuando el valor nulo es un valor nulo
En otras ocasiones, tener un valor nulo es correcto, está expresando la ausencia de algo. Debemos tratarlos para poder usar la tabla. Muchos modelos predictivos no pueden manejar tablas de entrada con valores faltantes.
En algunos casos, una variable es medida después de un período de tiempo, por lo que tenemos datos a partir de este momento y NA en las instancias previas.
A veces hay casos aleatorios, como una máquina que falla al recoletar datos o un usuario que se olvidó de completar algún campo en un formulario, entre otros.
Aquí aparece una pregunta importante: ¿Qué hacemos? 😱
Las siguientes recomendaciones son simplemente eso, recomendaciones. Pueden probar diferentes enfoques para descubrir cuál es la mejor estrategia para los datos que están analizando. No existe un “talle único y universal” en esto.
2.5.4 Excluir la fila entera
Si al menos una columna tiene un valor NA, excluyan la fila.
Es un método fácil y rápido, ¿no? Lo recomendamos cuando la cantidad de filas con valores faltantes sea baja. Pero, ¿cuán baja es baja? Eso depende de ustedes. Diez casos en 1,000 filas pueden no tener un gran impacto, a menos que esos 10 casos estén vinculados con la predicción de una anomalía; en esta instancia, representan información. Señalamos este tema en Caso 1: Reducción mediante la recategorización de valores menos representativos.
Ejemplo en R:
Inspeccionemos el conjunto de datos heart_disease con la función df_status, dado que uno de sus objetivos principales es ayudarnos con este tipo de decisiones.
library(dplyr)
library(funModeling)
df_status(heart_disease, print_results = F) %>% select(variable, q_na, p_na) %>% arrange(-q_na)## variable q_na p_na
## 1 num_vessels_flour 4 1.32
## 2 thal 2 0.66
## 3 age 0 0.00
## 4 gender 0 0.00
## 5 chest_pain 0 0.00
## 6 resting_blood_pressure 0 0.00
## 7 serum_cholestoral 0 0.00
## 8 fasting_blood_sugar 0 0.00
## 9 resting_electro 0 0.00
## 10 max_heart_rate 0 0.00
## 11 exer_angina 0 0.00
## 12 oldpeak 0 0.00
## 13 slope 0 0.00
## 14 heart_disease_severity 0 0.00
## 15 exter_angina 0 0.00
## 16 has_heart_disease 0 0.00q_na indica la cantidad de valores NA y p_na es el porcentaje. Pueden encontrar toda la información sobre la función df_status en el capítulo Análisis numérico, La voz de los números.
Dos variables tienen 4 y 2 filas con valores NA, entonces excluimos estas filas:
# na.omit devuelve el mismo data frame habiendo excluido todas las filas que contenían al menos un valor NA
heart_disease_clean=na.omit(heart_disease)
# número de filas antes de la exclusión:
nrow(heart_disease) ## [1] 303# número de filas después de la exclusión:
nrow(heart_disease_clean)## [1] 297Después de la exclusión, seis filas de 303 fueron eliminadas. Este enfoque parece adecuado para este conjunto de datos.
Sin embargo, existen otros escenarios en los que casi todos los casos son valores vacíos, por lo que ¡esta exclusión eliminaría todo el conjunto de datos!
2.5.5 Excluir la columna
En una operación similar al último caso, excluimos la columna. Si aplicamos el mismo razonamiento y la eliminación es sólo de unas pocas columnas y las restantes proveen un resultado final confiable, entonces es aceptable.
Ejemplo en R:
Estas exclusiones se pueden manejar fácilmente con la función df_status. El siguiente código va a conservar todos los nombres de las variables cuyo porcentaje de valores NA es mayor que 0.
# Obtener nombres de variables que contienen valores NA
vars_to_exclude=df_status(heart_disease, print_results = F) %>% filter(p_na > 0) %>% .$variable
# Verificar las variables a excluir
vars_to_exclude## [1] "num_vessels_flour" "thal"# Excluir las variables del conjunto de datos original
heart_disease_clean_2=select(heart_disease, -one_of(vars_to_exclude))2.5.6 Tratamiento de valores vacíos en variables categóricas
Abarcaremos diferentes perspectivas tanto para convertir como para tratar valores vacíos en variables nominales.
Los datos del siguiente ejemplo fueron derivados de web_navigation_data, que contiene información estándar sobre cómo llegan los usuarios a un determinado sitio web. Contiene source_page (la página desde la que proviene el usuario), landing_page (primera página visitada en el sitio), y country.
# Cuando lean los datos del ejemplo, presten atención
# al parámetro na.strings
web_navigation_data=
read.delim(file="https://goo.gl/dz7zNx",
sep="\t",
header = T,
stringsAsFactors=F,
na.strings="")2.5.6.1 Análisis numérico de los datos
stat_nav_data=df_status(web_navigation_data)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 source_page 0 0 50 51.5 0 0 character 5
## 2 landing_page 0 0 5 5.2 0 0 character 5
## 3 country 0 0 3 3.1 0 0 character 18Las tres variables tienen valores vacíos (NA). Falta casi la mitad de los valores en source_page, mientras que las otras dos variables tienen 5% y 3% de valores NA.
2.5.6.2 Caso A: Convertir el valor nulo en un string
En variables categóricas o nominales, el tratamiento más rápido es convertir el valor nulo en el string unknown. Así, el modelo de machine learning va a tomar los valores “vacíos” como otra categoría. Piénsenlo como una regla: “Si variable_X = unknown, entonces el resultado = sí”.
A continuación, proponemos dos métodos para cubrir los escenarios típicos:
Ejemplo en R:
library(tidyr)
# Método 1: Convertir una sola variable
web_navigation_data_1=web_navigation_data %>%
mutate(source_page =
replace_na(source_page,
"unknown_source")
)
# Método 2: Es una situación típica la de aplicar una
# función sólo a variables específicas y luego
# reingresarlas al data frame original
# Imaginen que queremos convertir todas las variables
# que tengan menos de 6% de valores NA:
vars_to_process =
filter(stat_nav_data, p_na<6)[,"variable"]
vars_to_process## [1] "landing_page" "country"# Crear un nuevo data frame con las variables
# transformadas
web_navigation_data_2=web_navigation_data %>%
mutate_at(.vars=vars(vars_to_process),
.funs=funs(replace_na(.,"other"))
)Verificar los resultados:
df_status(web_navigation_data_1)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 source_page 0 0 0 0.0 0 0 character 6
## 2 landing_page 0 0 5 5.2 0 0 character 5
## 3 country 0 0 3 3.1 0 0 character 18df_status(web_navigation_data_2)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 source_page 0 0 50 52 0 0 character 5
## 2 landing_page 0 0 0 0 0 0 character 6
## 3 country 0 0 0 0 0 0 character 19Nota: Aplicar una función a ciertas columnas es una tarea muy común en cualquier proyecto de datos. Hay más información sobre cómo utilizar la función mutate_at de dplyr aquí: How do I select certain columns and give new names to mutated columns?
2.5.6.3 Caso B: Asignar la categoría más frecuente
La intuición detrás de este método es agregar más de lo mismo para no afectar la variable. Sin embargo, a veces la afecta. No tendrá el mismo impacto si el valor más común aparece el 90% de las ocasiones que si aparece el 10%; es decir, depende de la distribución.
Hay otros escenarios en los que podemos incorporar nuevos valores faltantes basándonos en modelos predictivos como k-NN. Este enfoque es más apropiado que reemplazar por el valor más frecuente. No obstante, la técnica recomendada es la que vimos en Caso A: Convertir el valor nulo en un string.
2.5.6.4 Caso C: Excluir algunas columnas y transformar otras
El caso sencillo sería que la columna contenga, digamos, 50% de casos NA, dado que sería altamente probable que los datos no sean confiables.
En el caso que vimos antes, source_page tiene más de la mitad de los valores vacíos. Podríamos excluir esta variable y transformar -como lo hicimos- las otras dos.
El ejemplo está preparado como genérico:
# Configurar el umbral
threshold_to_exclude=50 # 50 Represents 50%
vars_to_exclude=filter(stat_nav_data, p_na>=threshold_to_exclude)
vars_to_keep=filter(stat_nav_data, p_na<threshold_to_exclude)
# Finalmente...
vars_to_exclude$variable## [1] "source_page"vars_to_keep$variable## [1] "landing_page" "country"# La próxima línea excluirá las variables que queden por encima del umbral y transformará las demás
web_navigation_data_3=select(web_navigation_data, -one_of(vars_to_exclude$variable)) %>%
mutate_at(.vars=vars(vars_to_keep$variable),
.funs=funs(replace_na(.,"unknown"))
)
# Verificar que no haya valores NA y que la variable que estaba por encima del umbral haya desaparecido
df_status(web_navigation_data_3)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 landing_page 0 0 0 0 0 0 character 6
## 2 country 0 0 0 0 0 0 character 192.5.6.5 Resumiendo
¿Qué pasa si los datos tienen 40% de valores NA? Depende del objetivo del análisis y de la naturaleza de los datos.
Lo importante aquí es “salvar” la variable para poder usarla. Es común encontrar muchas variables con valores faltantes. Puede que esas variables incompletas contengan información útil para la predicción cuando tienen un valor, por lo tanto, debemos tratarlas y luego construir un modelo predictivo.
De todas maneras, debemos minimizar el sesgo que estamos introduciendo porque el valor faltante es un valor que “no está ahí”.
- Cuando estamos haciendo un informe, la sugerencia es reemplazar
NAcon el stringempty, - Cuando estamos haciendo un modelo predictivo que se está corriendo en el momento, la recomendación es asignar la categoría que más se repite.
2.5.7 ¿Hay algún patrón en los valores faltantes?
Primero, carguemos los datos de ejemplo de películas y hagamos un análisis rápido.
# Lock5Data contiene muchos data frames para practicar
# install.packages("Lock5Data")
library(Lock5Data)
# Cargar datos
data("HollywoodMovies2011")
# Análisis numérico
df_status(HollywoodMovies2011)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 Movie 0 0.00 0 0.00 0 0 factor 136
## 2 LeadStudio 0 0.00 0 0.00 0 0 factor 34
## 3 RottenTomatoes 0 0.00 2 1.47 0 0 integer 75
## 4 AudienceScore 0 0.00 1 0.74 0 0 integer 60
## 5 Story 0 0.00 0 0.00 0 0 factor 22
## 6 Genre 0 0.00 0 0.00 0 0 factor 9
## 7 TheatersOpenWeek 0 0.00 16 11.76 0 0 integer 118
## 8 BOAverageOpenWeek 0 0.00 16 11.76 0 0 integer 120
## 9 DomesticGross 0 0.00 2 1.47 0 0 numeric 130
## 10 ForeignGross 0 0.00 15 11.03 0 0 numeric 121
## 11 WorldGross 0 0.00 2 1.47 0 0 numeric 134
## 12 Budget 0 0.00 2 1.47 0 0 numeric 60
## 13 Profitability 1 0.74 2 1.47 0 0 numeric 134
## 14 OpeningWeekend 1 0.74 3 2.21 0 0 numeric 130Observemos los valores presentes en la columna p_na. Hay un patrón en los valores faltantes: cuatro variables tienen 1.47% de valores NA y otras cuatro tienen cerca de 11.7%. En este caso, no podemos chequear la fuente de los datos; sin embargo, es una buena idea verificar si esos casos tienen un problema en común.
2.5.8 Tratar valores faltantes en variables numéricas
Nuestro primer acercamiento a este punto al principio del capítulo fue convertir todos los valores de NA a 0.
Una solución es reemplazar los valores vacíos por la media, la mediana u otros criterios. Sin embargo, tenemos que ser conscientes del cambio que esto genera en la distribución.
Si vemos que la variable parece estar correlacionada cuando no está vacía (igual que la categórica), entonces un método alternativo es crear segmentos, convirtiéndola así en categórica.
2.5.8.1 Método 1: Convertir la variable a categórica
La función equal_freq divide la variable en los segmentos deseados. Toma una variable numérica (TheatersOpenWeek) y devuelve una categórica (TheatersOpenWeek_cat), basándose en el criterio de igual frecuencia.
Figure 2.26: Valores faltantes en datos categóricos
## TheatersOpenWeek_cat frequency percentage cumulative_perc
## 1 [ 3,2408) 24 18 18
## 2 [2408,2904) 24 18 35
## 3 [2904,3114) 24 18 53
## 4 [3114,3507) 24 18 71
## 5 [3507,4375] 24 18 88
## 6 <NA> 16 12 100Como podemos ver, TheatersOpenWeek_cat contiene cinco segmentos de 24 casos cada uno, cada uno representa el ~18% de los casos totales. Pero, los valores NA siguen ahí.
Por último, debemos convertir los NA en el string empty.
Y eso es todo: la variable está lista para usar.
Cortes personalizados:
Si queremos usar tamaños personalizados de segmentos en lugar de los que vienen dados por la igual frecuencia, podemos usar la función cut. En este caso toma la variable numérica TheatersOpenWeek y devuelve TheatersOpenWeek_cat_cust.
# Desactivar la notación científica en la sesión actual
# de R
options(scipen=999)
# Crear segmentos personalizados, con límites en 1,000,
# 2,300, y un máx de 4,100. Los valores por encima de
# 4,100 serán asignados a NA.
HollywoodMovies2011$TheatersOpenWeek_cat_cust=
cut(HollywoodMovies2011$TheatersOpenWeek,
breaks = c(0, 1000, 2300, 4100),
include.lowest = T,
dig.lab = 10)
freq(HollywoodMovies2011$TheatersOpenWeek_cat_cust,
plot = F)## var frequency percentage cumulative_perc
## 1 (2300,4100] 94 69.1 69
## 2 <NA> 19 14.0 83
## 3 (1000,2300] 14 10.3 93
## 4 [0,1000] 9 6.6 100Debemos destacar que la segmentación por igual frecuencia tiende a ser más robusta que la igual distancia que divide la variable, que se basa en tomar el mínimo y el máximo, y la distancia entre cada segmento, sin considerar cuántos casos caen en cada segmento.
La igual frecuencia ubica a los valores atípicos en el primer o último segmento según corresponda. Los valores normales pueden ir desde 3 hasta 20 segmentos. Un alto número de segmentos suele significar más ruido. Para leer más, diríjanse al capítulo de cross_plot.
2.5.8.2 Método 2: Completar el NA con algún valor
Al igual que con las variables categóricas, podemos reemplazar los valores con un número como el promedio o la mediana.
En este caso, reemplazaremos los valores NA por el promedio y graficar los resultados del antes y el después lado a lado.
# Completar todos los valores NA con el promedio de
# la variable
HollywoodMovies2011$TheatersOpenWeek_mean=
ifelse(is.na(HollywoodMovies2011$TheatersOpenWeek),
mean(HollywoodMovies2011$TheatersOpenWeek,
na.rm = T),
HollywoodMovies2011$TheatersOpenWeek
)
# Graficar la variable original
p1=ggplot(HollywoodMovies2011, aes(x=TheatersOpenWeek)) +
geom_histogram(colour="black", fill="white") +
ylim(0, 30)
# Graficar la variable transformada
p2=ggplot(HollywoodMovies2011,
aes(x=TheatersOpenWeek_mean)
) +
geom_histogram(colour="black", fill="white") +
ylim(0, 30)
# Ubicar los gráficos lado a lado
library(gridExtra)
grid.arrange(p1, p2, ncol=2)
Figure 2.27: Completando los NA con el valor promedio
Podemos ver un pico en 2828, que es producto de la transformación. Se introduce un sesgo alrededor de este punto. Si estamos prediciendo algún evento, entonces sería más seguro no tener ningún evento especial cerca de este punto.
Por ejemplo, si estamos prediciendo un evento binario y el evento menos representativo está correlacionado con tener un promedio de 3000 en TheatersOpenWeek, entonces las probabilidades de tener una Tasa de falsos positivos pueden ser más altas. De nuevo, esto se relaciona con el capítulo de Variables de alta cardinalidad en estadística descriptiva.
Como un comentario extra con respecto a la ultima visualización, fue importante configurar el máximo del eje-y en 30 para que los dos gráficos fueran comparables entre sí.
Como pueden ver, existe una interrelación entre todos los conceptos. 😉.
2.5.8.3 Eligiendo el valor adecuado para completar
En el último ejemplo remplazamos los valores NA con el promedio, ¿pero qué pasa si usamos otros valores? Depende de la distribución de la variable.
La variable que usamos (TheatersOpenWeek) parece tener una distribución normal, que es la razón por la cual utilizamos el promedio. No obstante, si la variable está más sesgada, entonces otra métrica sería más adecuada; por ejemplo, la mediana es menos sensible a los valores atípicos.
2.5.9 Métodos avanzados de imputación
Ahora vamos a hacer un repaso rápido de métodos de imputación más sofisticados en los que creamos un modelo predictivo, con todo lo que eso implica.
2.5.9.1 Método 1: Usando random forest (missForest)
La funcionalidad del paquete missForest se basa en random forest para completar cada valor faltante en un proceso iterativo, manejando variables categóricas y numéricas simultáneamente.
Más allá de la imputación de valores faltantes, el modelo de bosque aleatorio tiene uno de los mejores desempeños con muchos tipos distintos de datos.
En el siguiente ejemplo, completaremos los datos de HollywoodMovies2011 con los que estábamos trabajando antes. Estos datos contienen valores NA tanto en variables numéricas como categóricas.
# install.packages("missForest")
library(missForest)
# Copiar los datos
df_holly=Lock5Data::HollywoodMovies2011
# Volver a crear la TheatersOpenWeek_cat_cust
df_holly$TheatersOpenWeek_cat_cust=
cut(HollywoodMovies2011$TheatersOpenWeek,
breaks = c(0, 1000, 2300, 4100),
include.lowest = T,
dig.lab = 10)
# Vamos a introducir 15% más de valores NA en
# TheatersOpenWeek_3 para producir un mejor ejemplo.
# La función prodNA en missForest nos va a ayudar.
# Configurar seed para obtener siempre la misma
# cantidad de valores NA
set.seed(31415)
df_holly$TheatersOpenWeek_cat_cust=
prodNA(
select(df_holly, TheatersOpenWeek_cat_cust),
0.15
)[,1]
# Excluir las variables que no son útiles
df_holly=select(df_holly, -Movie)
# ¡Ahora la magia! Imputar el data frame
# xmis parameter=los datos con valores faltantes
imputation_res=missForest(xmis = df_holly)## missForest iteration 1 in progress...done!
## missForest iteration 2 in progress...done!
## missForest iteration 3 in progress...done!
## missForest iteration 4 in progress...done!# data frame final completado
df_imputed=imputation_res$ximpNota: missForest fallará si tiene alguna variable carácter.
Ahora es momento de comparar las distribuciones de algunas de las variables imputadas, usaremos la variable original previa a la discretización: TheatersOpenWeek. Si todo sale bien, se verán parecidas en un análisis visual.
# Crear otra imputación basada en na.rougfix del paquete randomForest
df_rough=na.roughfix(df_holly)
# Comparar distribuciones antes y después de la imputación
df_holly$imputation="original"
df_rough$imputation="na.roughfix"
df_imputed$imputation="missForest"
# Poner los dos data frames en uno solo, pero dividido por la variable is_imputed
df_all=rbind(df_holly, df_imputed, df_rough)
# Convertir a factor para utilizarla en un gráfico
df_all$imputation=factor(df_all$imputation, levels=unique(df_all$imputation))
# Graficar
ggplot(df_all, aes(TheatersOpenWeek, colour=imputation)) + geom_density() + theme_minimal() + scale_colour_brewer(palette="Set2")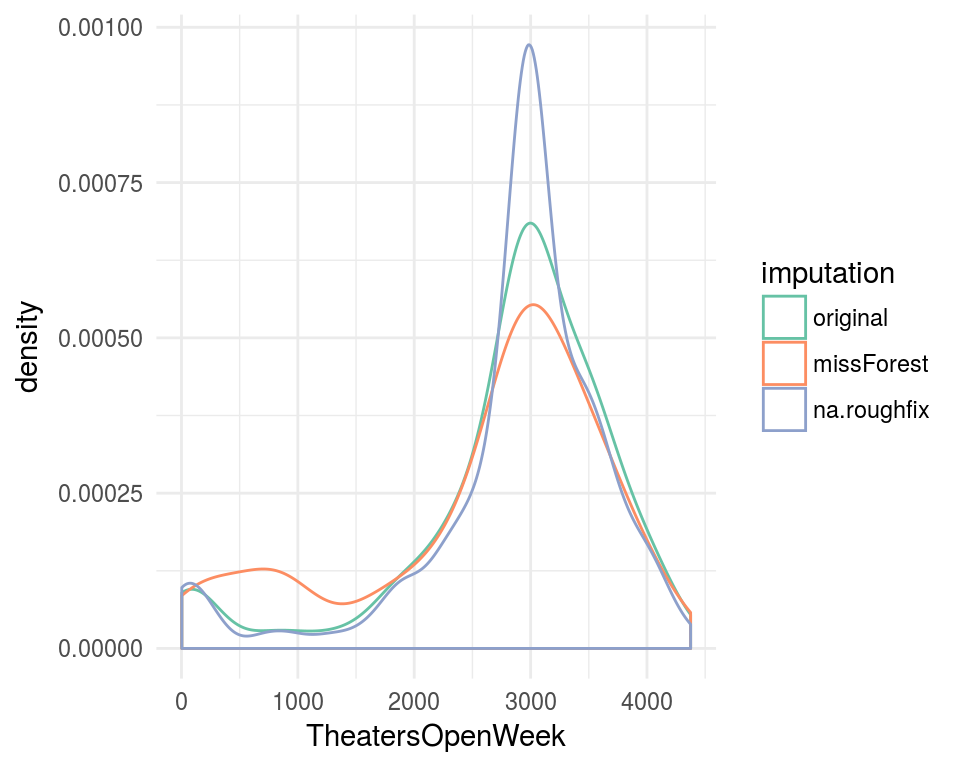
Figure 2.28: Comparación de métodos de imputación (variable numérica)
- La curva naranja muestra la distribución después de la imputación basada en el paquete
missForest. - La azul muestra el método de imputación que vimos al principio, que reemplaza todos los valores
NApor la mediana usando la funciónna.roughfixdel paqueterandomForest. - La verde muestra la distribución sin ninguna imputación (por supuesto, los valores NA no están expuestos).
Análisis:
Reemplazar los valores NA por la mediana tiende a concentrar, como era de esperarse, todos los valores cerca de 3000. Por otro lado, la imputación realizada por el paquete missForest provee una distribución más natural porque no concentra los valores cerca de un solo valor. Es por eso que el pico alrededor de 3000 es más bajo que el original.
¡La curva naranja y la verde son bastante parecidas!
Si deseamos tomar un punto de vista analítico, podemos realizar una prueba estadística para comparar, por ejemplo, los promedios o las varianzas.
A continuación vamos a visualizar la variable discretizada y personalizada de TheatersOpenWeek (TheatersOpenWeek_cat_cust).
# Un truco feo para graficar NA como una categoría
levels(df_all$TheatersOpenWeek_cat_cust)=
c(levels(df_all$TheatersOpenWeek_cat_cust), "NA")
flag_na=is.na(df_all$TheatersOpenWeek_cat_cust)
df_all$TheatersOpenWeek_cat_cust[flag_na]="NA"
# ¡Ahora el gráfico!
ggplot(df_all, aes(x = TheatersOpenWeek_cat_cust,
fill = TheatersOpenWeek_cat_cust)
) +
geom_bar(na.rm=T) +
facet_wrap(~imputation) +
geom_text(stat='count',
aes(label=..count..),
vjust=-1) +
ylim(0, 125) +
scale_fill_brewer(palette="Set2") +
theme_minimal() +
theme(axis.text.x=
element_text(angle = 45, hjust = 0.7)
) +
theme(legend.position="bottom")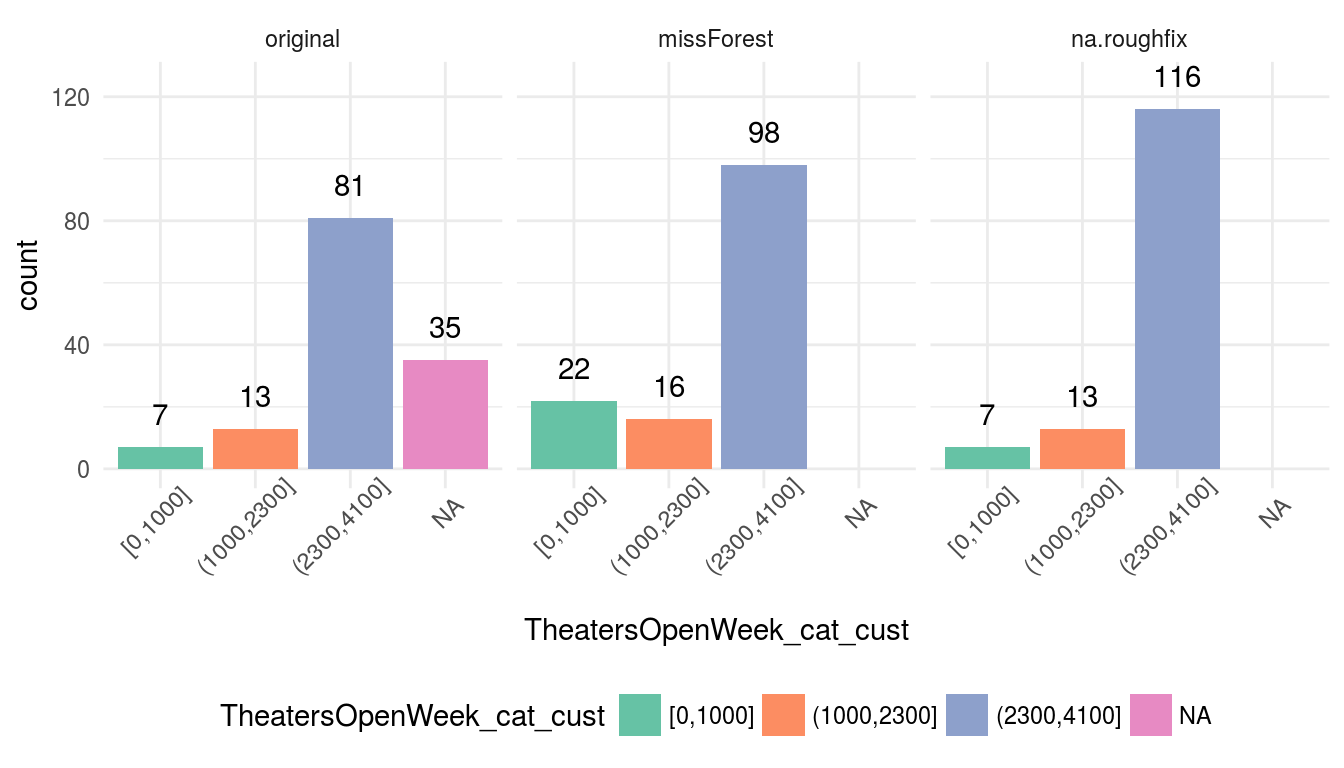
Figure 2.29: Comparación de métodos de imputación
Análisis:
La variable original contiene 35 valores NA que fueron reemplazados con la moda o el valor más frecuente en na.roughfix: (2300, 4100]. Por otro lado, obtuvimos un resultado apenas diferente al utilizar missForest, que completó los valores basándose en otras variables.
missForest agregó 15 filas en la categoría [0, 1000], 3 en [1000, 2300], y 17 en la categoría [2300, 4100].
2.5.9.2 Método 2: Usar el enfoque MICE
Consejo: Como primer abordaje en la imputación de los valores faltantes, este método es sumamente complejo. 😨.
MICE significa “Imputación Multivariada por ecuaciones encadenadas” (“Multivariate Imputation by Chained Equations” en inglés), también se la conoce como “Especificación totalmente condicional” (“Fully Conditional Specification”). Este libro cubre este tema debido a su popularidad.
MICE implica un marco completo para analizar y lidiar con los valores faltantes. Considera las interacciones entre todas las variables al mismo tiempo (multivariado y no una sola) y basa su funcionalidad en un proceso iterativo que utiliza diferentes modelos predictivos para completar cada variable.
Internamente, completa la variable A, basada en B y C. Luego, llena B basada en A y C (A se predice previamente) y la iteración continúa. El nombre “ecuaciones encadenadas” viene del hecho de que podemos especificar el algoritmo por variable para imputar los casos.
Esto crea réplicas M de los datos originales sin que falten valores. Pero, ¿por qué crear réplicas M?
En cada réplica, la decisión de qué valor insertar en el espacio vacío se basa en la distribución.
Muchas demostraciones de MICE se enfocan en validar la imputación y en utilizar los modelos predictivos que apoyan el paquete, que son pocos. Esto es genial si no queremos usar otros modelos predictivos (random forest, gradient boosting machine, etc.), o una técnica de validación cruzada (p.e.,‘caret’).
La técnica MICE pone el resultado final al establecer una función pool() que promedia los parámetros (o betas) de los modelos predictivos M proporcionando facilidades para medir la varianza debido a valores faltantes.
Sí, un modelo por cada data frame generado. Suena como bagging, ¿no? Pero no tenemos esta posibilidad con los modelos mencionados.
MICE tiene muchas funciones que nos ayudan a procesar y validar los resultados de la compleción. Pero, para mantenerlo muy simple, cubriremos sólo una pequeña parte de ellas. El siguiente ejemplo se centrará en la extracción de un data frame sin valores faltantes, listo para ser utilizado con otros programas o modelos predictivos.
Ejemplo en R:
Esto imputará los datos del data frame nhanes que viene incluido en mice package. Veámoslo:
# install.packages("mice")
library(mice)
df_status(nhanes)## variable q_zeros p_zeros q_na p_na q_inf p_inf type unique
## 1 age 0 0 0 0 0 0 numeric 3
## 2 bmi 0 0 9 36 0 0 numeric 16
## 3 hyp 0 0 8 32 0 0 numeric 2
## 4 chl 0 0 10 40 0 0 numeric 13Tres variables tienen valores faltantes. Vamos a completarlos:
# La imputación por defecto crea cinco conjuntos de datos completos
imp_data=mice(nhanes, m = 5, printFlag = FALSE)
# Obtener el conjunto de datos final que contiene los cinco data frames imputados, número total de filas==nrow(nhanes)*5
data_all=complete(imp_data, "long")
# data_all contiene las mismas columnas que nhanes más dos adicionales: .id y .imp
# .id=filas de la 1 a la 25
# .imp=imputar el data frame .id 1 a 5 (parámetro m)En los datos originales, nhanes tiene 25 filas y data_all tiene 125 filas, que es el resultado de crear 5 (m=5) data frames completos de 25 filas cada uno.
Es hora de chequear los resultados:
densityplot(imp_data)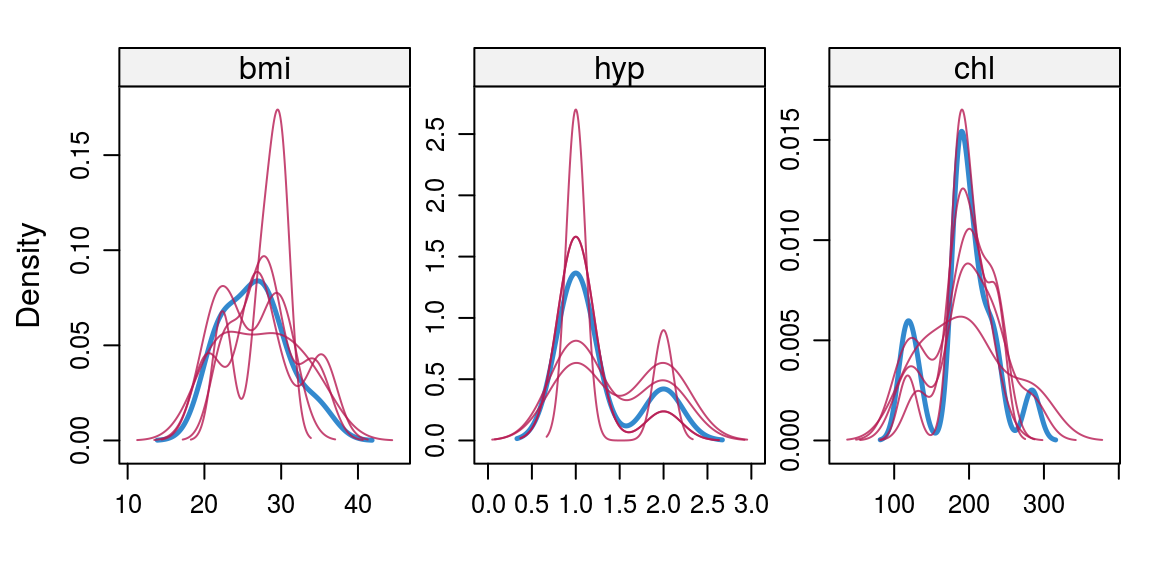
Figure 2.30: Analizar los valores faltantes usando MICE
Cada línea roja muestra la distribución de cada data frame imputado y la línea azul contiene la distribución original. La idea detrás de esto es que si se ven similares, entonces la imputación sigue la distribución original.
Por ejemplo, chl contiene un data frame completado; por lo tanto, sólo una línea roja con dos picos alrededor de dos valores muy superiores a los originales.
El inconveniente es que se trata de un proceso lento que puede requerir ciertos ajustes finos para funcionar. Por ejemplo: mice_hollywood=mice(HollywoodMovies2011, m=5) fallará después de algún tiempo de procesarlo y es un data frame pequeño.
Más información sobre el paquete MICE:
- Paper original sobre MICE: Multivariate Imputation by Chained Equations in R
- Handling missing data with MICE package; a simple approach
2.5.10 Conclusiones
Habiendo cubierto todas las opciones, podríamos preguntar: ¿cuál es la mejor estrategia? Bueno, depende de cuánto queramos intervenir para manejar los valores faltantes.
Un pequeño repaso de las estrategias posibles:
Excluir las filas y columnas con valores faltantes. Sólo es aplicable si hay pocas filas (o columnas) con valores faltantes, y los datos restantes son suficientes para alcanzar la meta del proyecto. No obstante, cuando excluimos filas con valores faltantes y creamos un modelo predictivo que va a ejecutarse en producción, si llega un caso nuevo que contiene valores faltantes, debemos asignar un valor para procesarlos.
Las estrategias de convertir variables numéricas a categóricas y luego crear el valor “empty” (también aplicable a las variables categóricas), es la opción más rápida -y recomendada- para lidiar con valores nulos. De esta manera incorporamos los valores faltantes al modelo para que pueda manejar la incertidumbre.
Los métodos de imputación como los que cubrimos con MICE y missForest son considerablemente más complejos. Con estos métodos, introducimos un sesgo controlado para no tener que excluir filas o columnas.
Es un arte encontrar el equilibrio correcto entre profundizar en estas transformaciones y mantenerlo simple. El tiempo invertido puede no reflejarse en la precisión global.
Independientemente del método, es muy importante analizar el impacto de cada decisión. Hay mucho de prueba y error, así como análisis exploratorio de datos, que conduce al descubrimiento del método más adecuado para sus datos y proyecto.

2.6 Consideraciones que involucran al tiempo
2.6.1 ¿De qué se trata esto?

Todo cambia y nada permanece. - Heráclito, (535 - 475 AC), filósofo griego presocrático.
Lo mismo ocurre con las variables.
Con el paso del tiempo, las variables pueden cambiar sus valores, haciendo que el análisis del tiempo sea crucial a la hora de crear un modelo predictivo. Así evitamos tomar los efectos como causas.
¿Qué vamos a repasar en este capítulo?
- Conceptos de filtrado de información antes del evento a predecir.
- Cómo analizar y preparar las variables que aumentan -o disminuyen- su valor hasta el infinito (y más allá).
2.6.1.1 No utilicen información del futuro

Imagen de la película: “Volver al futuro” (1985). Robert Zemeckis (Director).
Usar una variable que contiene información después del evento que se está prediciendo es un error común cuando se comienza un nuevo proyecto de modelo predictivo, como jugar a la lotería hoy usando el periódico de mañana.
Imaginemos que necesitamos construir un modelo predictivo para saber qué usuarios es probable que adquieran una suscripción completa en una aplicación web, y este software tiene una funcionalidad ficticia llamada feature_A:
## user_id feature_A full_subscription
## 1 1 yes yes
## 2 2 yes yes
## 3 3 yes yes
## 4 4 no no
## 5 5 yes yes
## 6 6 no no
## 7 7 no no
## 8 8 no no
## 9 9 no no
## 10 10 no noCreamos el modelo predictivo, obtuvimos una precisión perfecta, y una inspección arroja el siguiente mensaje: “El 100% de los usuarios que tienen una suscripción completa utiliza la característica Feature A”. Algunos algoritmos predictivos reportan la importancia de las variables; por lo que feature_A estará por encima del resto.
El problema es: feature_A solo está disponible después de que el usuario adquiere la suscripción completa. Por lo tanto, no puede ser utilizada.
El mensaje clave es: No confíen en variables perfectas, ni modelos perfectos.
2.6.1.2 Sean justos con los datos, dejen que desarrollen su comportamiento
Como en la naturaleza, las cosas tienen un tiempo mínimo y máximo para empezar a mostrar cierto comportamiento. Este tiempo oscila de 0 a infinito. En la práctica se recomienda estudiar cuál es el mejor período para analizar, es decir, podemos excluir todo el comportamiento antes y después de este período de observación. Establecer rangos en las variables no es sencillo, ya que puede ser un poco subjetivo.
Imaginen que tenemos una variable numérica que aumenta a medida que pasa el tiempo. Es posible que necesitemos definir una ventana de tiempo de observación para filtrar los datos y alimentar el modelo predictivo.
- Configurar el tiempo mínimo: ¿Cuánto tiempo es necesario para empezar a ver el comportamiento?
- Configurar el tiempo máximo: ¿Cuánto tiempo es necesario para ver el final del comportamiento?
La solución más fácil es: configurar el mínimo en el principio y el máximo en toda la historia.
Estudio de caso:
Dos personas, Ouro y Borus, son usuarios de una aplicación web que tiene una determinada funcionalidad llamada feature_A, y necesitamos crear un modelo predictivo que pronostique basándose en el uso de feature_A usage -medido en clicks- si una persona va a adquirir full_subscription.
Los datos actuales dicen: Borus tiene full_subscription, mientras que Ouro no.
Figure 2.31: Tengan cuidado con las consideraciones que involucran el tiempo
El usuario Borus comienza a usar feature_A a partir del día 3, y después de 5 días ella le da más uso -15 clicks vs. 12- a esta función que Ouro, que comenzó a usarla desde el día 0.
Si Borus adquiere full subscription y Ouro no, ¿qué aprenderá el modelo?
Cuando modelamos con la historia completa -days_since_signup = all-, cuanto más alto sea days_since_signup mayor será probabilidad, dado que Borus tiene el número más alto.
Sin embargo, si sólo tomamos la historia de los usuarios de los primeros 5 días desde la suscripción, la conclusión será la opuesta.
¿Por qué conservar los primeros 5 días de la historia?
El comportamiento durante este período inicial (kick-off) puede ser más relevante -con respecto a la precisión de la predicción- que analizar toda la historia. Como dijimos antes, depende de cada caso.
2.6.1.3 Luchar contra el infinito
El número de ejemplos sobre este tema es muy amplio. Mantengamos la esencia de este capítulo en cómo cambian los datos a lo largo del tiempo. A veces es sencillo, como una variable que alcanza su mínimo (o máximo) después de un tiempo fijo. Este caso es fácilmente alcanzable.
Por otro lado, requiere que el ser humano luche contra el infinito.
Consideren el siguiente ejemplo. ¿Cuántas horas se necesitan para alcanzar el valor 0?
¿Qué tal 100 horas?
Figure 2.32: 100 horas
Hmm chequeemos el valor mínimo…
## [1] "Min value after 100 hours: 0.22"Está cerca de cero, pero ¿qué pasa si esperamos 1000 horas?
Figure 2.33: 1,000 horas
## [1] "Min value after 1,000 hours: 0.14"¡Hurra! ¡Nos estamos acercando! De 0.21 a 0.14. Pero ¿qué pasa si esperamos 10 veces más? (10,000 horas)
Figure 2.34: 10,000 horas
## [1] "Min value after 10,000 hours: 0.11"¡Seguimos sin llegar a cero! ¡¿Cuánto tiempo necesitamos?! 😱
Como habrán notado, es probable que lleguemos a cero en el infinito… Estamos ante una Asíntota.
¿Qué debemos hacer? Es momento de pasar a la siguiente sección.
2.6.1.4 Amigarnos con el infinito
En el último ejemplo vimos el análisis de la antigüedad de un consumidor en una compañía. Este valor puede ser infinito.
Por ejemplo, si el objetivo del proyecto es predecir un resultado binario, como buy/don't buy, un análisis útil es calcular la tasa de buy de acuerdo a la antigüedad del usuario. Llegaremos a conclusiones como: En promedio, un consumidor necesita cerca de 6 meses para comprar este producto.
Esta respuesta puede alcanzarse gracias al trabajo conjunto del científico de datos y un experto en la materia.
En este caso, un cero puede considerarse al igual que el valor que tenga el 95% de la población. En términos estadísticos, es el percentil 0.95. Este libro abarca extensamente este tema en Anexo 1: La magia de los percentiles. Es un tema clave en el análisis exploratorio de datos.
Un caso relacionado es el de lidiar con valores atípicos, cuando aplicamos percentiles como criterio de corte, como vimos en el capítulo Tratamiento de valores atípicos.
2.6.1.5 Ejemplos en otras áreas
Es muy común encontrar este tipo de variables en muchos conjuntos o proyectos de datos.
En medicina, en los proyectos de análisis de supervivencia, los médicos suelen definir un umbral de, por ejemplo, 3 años para considerar que un paciente sobrevive al tratamiento.
En proyectos de marketing, si un usuario disminuye su actividad dentro de un cierto umbral, digamos: * 10-clicks en el sitio web de la compañía en el último mes * No abrir un email después de 1 semana * Él o ella no compra por 30 días
Se lo puede definir como la pérdida de un cliente u oportunidad.
En atención al cliente, un problema puede marcarse como resuelto una vez que la persona pasó 1 semana sin reportar nuevas quejas.
En el análisis de señales cerebrales, si estas señales provienen de la corteza visual en un proyecto en el que, por ejemplo, necesitamos predecir qué tipo de imagen está mirando el paciente, entonces los primeros 40ms de valores no sirven porque es el tiempo que el cerebro necesita para empezar a procesar la señal.
Pero esto también ocurre en “la vida real”, como cuando escribimos un libro de análisis de datos para todas las edades, ¿cuánto tiempo necesitamos para terminarlo? ¿Una cantidad infinita? Probablemente no. 😄.
2.6.1.6 Reflexiones finales
Definir un periodo de tiempo para crear un conjunto de entrenamiento y validación, implica un sesgo importante en nuestros datos. Al igual que decidir cómo manejar las variables que cambian con el tiempo. Es por eso que el Análisis exploratorio de datos es importante para entrar en contacto con los datos que estamos analizando.
Los temas están interconectados. Ahora es momento de mencionar la relación de este capítulo con la Validación out-of-time. Cuando predecimos eventos en el futuro, debemos analizar cuánto tiempo es necesario para que la variable objetivo cambie.
El concepto clave aquí es: cómo manejar el tiempo en modelado predictivo. Es una buena oportunidad para preguntar: ¿Cómo sería posible abordar estos problemas del tiempo con sistemas automáticos?
El conocimiento humano es crucial en estos contextos para definir umbrales basándonos en la experiencia, intuición y algunos cálculos.
