4 Evaluar el desempeño de un modelo

Este capítulo cubre aspectos metodológicos del error en los modelos predictivos, cómo medirlo a través de validación cruzada de los datos y su similitud con la técnica de bootstrapping. Y cómo estas estrategias son utilizadas internamente por algunos modelos predictivos como random forests o gradient boosting machines.

También hay un capítulo sobre cómo validar los modelos cuando el tiempo es un factor influyente, que es similar a la validación clásica de entrenamiento/prueba.

4.1 Conociendo el error

Aspectos metodológicos de la validación de modelos

4.1.1 ¿De qué se trata esto?

Una vez que construimos un modelo predictivo, ¿cómo sabemos si su calidad es buena? ¿Capturó -información- sobre patrones generales (excluyendo el -ruido-)?

4.1.1.1 ¿Qué tipo de datos?

Tiene un enfoque distinto del que veremos en la validación out-of-time. Este enfoque podría utilizarse incluso cuando no sea posible filtrar los casos por fecha, por ejemplo, teniendo un pantallazo de los datos en un momento determinado, cuando no se generará nueva información.

Por ejemplo, una investigación de datos de salud de una cantidad reducida de personas, una encuesta, o algunos datos disponibles en Internet para prácticas. Es caro, poco práctico, poco ético o incluso imposible agregar nuevos casos. Los datos de heart_disease que vienen en el paquete funModeling son un ejemplo.

4.1.2 Reducir comportamientos inesperados

Cuando un modelo es entrenado, solo ve una parte de la realidad. Es una muestra de una población que no se puede ver entera.

Hay muchas maneras de validar un modelo (Precisión / Curvas ROC / Lift / Ganancia / etc). Cualquiera de estas métricas están ligadas a la varianza, lo que implica obtener valores diferentes. Si eliminamos algunos casos y luego ajustamos un nuevo modelo, veremos un valor ligeramente diferente.

Imaginemos que construimos un modelo y logramos una precisión de 81, ahora quitamos el 10% de los casos, y luego ajustamos uno nuevo, la precisión ahora es: 78.4. ¿Cuál es la precisión real? ¿La que se obtiene con el 100% de los datos o la que se basa en el 90%? Por ejemplo, si el modelo se ejecuta en vivo en un entorno de producción, verá otros casos y el punto de precisión se moverá hacia uno nuevo.

Entonces, ¿cuál es el valor real, el que reportaremos? Las técnicas de remuestreo y validación cruzada se promedian -basándose en diferentes criterios de muestreo y prueba- con el fin de obtener una aproximación al valor más confiable.

Pero, ¿por qué quitar casos?

No tiene sentido eliminar casos como ese, pero da una idea de cuán sensible es la métrica de precisión, recuerden que estamos trabajando con una muestra de una población desconocida.

Si tuviéramos un modelo totalmente determinista, un modelo que contenga el 100% de todos los casos que estamos estudiando, y las predicciones fueran 100% exactas en todos los casos, no necesitaríamos todo esto.

En la medida en que siempre analizamos las muestras, sólo necesitamos acercarnos a la verdad real y desconocida de los datos a través de la repetición, el remuestreo, la validación cruzada, etc…

4.1.3 Ilustremos esto con Cross Validation (CV)

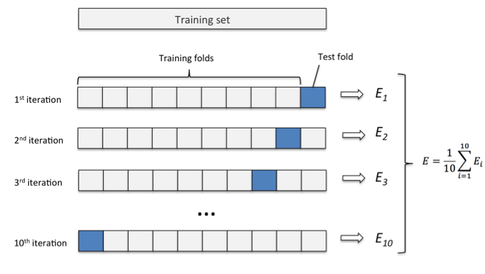
Figure 4.1: k-fold Cross Validation

Crédito de la imagen: Sebastian Raschka Ref. (Raschka 2017)

4.1.3.1 Breve resumen sobre CV

Divide los datos en grupos aleatorios, digamos 10, de igual tamaño. Estos grupos son comúnmente llamados folds o pliegues, representados por la letra 'k'.
Tomen 9 pliegues, construyan un modelo, y luego apliquen el modelo al pliegue restante (el que dejaron fuera). Esto nos devolverá la métrica de precisión que queremos: precisión (accuracy), ROC, Kappa, etc. En este ejemplo estamos usando la precisión.
Repitan esto k veces (10 en nuestro ejemplo). Así conseguiremos 10 precisiones diferentes. El resultado final será el promedio de todos ellos.

Este promedio será el que evalúe si un modelo es bueno o no, y también si incluirlo o no en un informe.

4.1.3.2 Ejemplo práctico

Hay 150 filas en el data frame iris, usar el paquete caret para construir un random forest con caret usando cross-validation llevará a la construcción -interna- de 10 bosques aleatorios, cada uno basado en 135 filas (9/10 * 150), y reportando una precisión basada en los 15 casos restantes (1/10 * 150). Este procedimiento se repite 10 veces.

Esta parte del resultado:

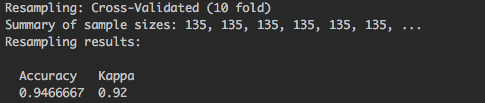
Figure 4.2: Resultado de la validación cruzada de caret

Summary of sample sizes: 135, 135, 135, 135, 135, 135, ..., cada 135 representa una muestra de entrenamiento, 10 en total pero el resultado está truncado.

En lugar de un solo número -el promedio-, podemos ver una distribución:

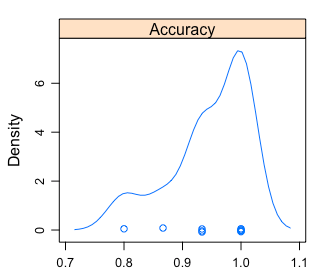
Figure 4.3: Análisis visual de la distribución de la precisión

Figure 4.4: Distribución de la precisión

La precisión mín/máx estará entre ~0.8 y ~1.
El promedio es el que reportó caret.
El 50% de las veces estará en el rango entre ~0.93 y ~1.

Lectura recomendada por Rob Hyndman, creador del paquete forecast: Why every statistician should know about cross-validation? (Hyndman 2010)

4.1.4 Pero, ¿qué es el error?

La suma del Sesgo, Varianza y el error no explicado -ruido interno- en los datos, o el que el modelo jamás podrá reducir.

Estos tres elementos constituyen el error reportado.

4.1.4.1 ¿Cuál es la naturaleza del Sesgo (bias) y la Varianza?

Cuando el modelo no funciona bien, puede haber varias causas:

Modelo demasiado complicado: Digamos que tenemos muchas variables de entrada, que se relaciona con una alta varianza. El modelo sobreajustará los datos de entrenamiento, teniendo una baja precisión sobre datos nunca vistos debido a su particularización.
Modelo demasiado sencillo: Por otro lado, puede que el modelo no esté capturando toda la información que hay en los datos debido a su simpleza. Esto está relacionado con un alto sesgo.
Datos de entrada insuficientes: Los datos crean formas en un espacio n-dimensional (donde n es todas las variables de entrada+objetivo). Si no hay suficientes puntos, esta forma no se desarrolla bien.

Hay más información sobre esto en “In Machine Learning, What is Better: More Data or Better Algorithms” (Amatriain 2015).

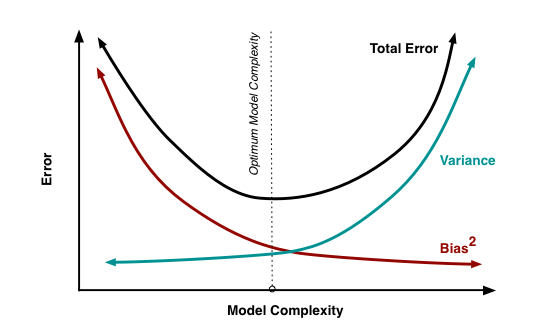
Figure 4.5: Equilibrio entre sesgo y varianza

Crédito de la imagen: Scott Fortmann-Roe (Fortmann 2012). También contiene una forma intuitiva de entender el error a través del sesgo y la varianza mediante una animación.

4.1.4.2 Equilibrio entre complejidad y precisión

El sesgo y la varianza están relacionados en el sentido de que si uno baja, el otro sube, por lo que hay un equilibrio entre ellos. Un ejemplo práctico de esto se ve en la medida de calidad de modelos llamada Criterio de Información de Akaike (AIC por Akaike Information Criterion, en inglés).

El AIC se utiliza como heurística para elegir el mejor modelo de series temporales en la función auto.arima dentro del paquete forecast en R (Hyndman 2017). Elige el modelo que tenga el AIC más bajo.

Cuanto más bajo, mejor: La precisión en la predicción reducirá el valor, mientras que el número de parámetros lo aumentará.

4.1.4.3 Bootstrapping vs Validación cruzada

Bootstrapping suele utilizarse para estimar un parámetro.
Validación cruzada se utiliza para elegir entre distintos modelos predictivos.

Nota: Para un abordaje más profundo sobre sesgo y varianza, por favor refiéranse a (Fortmann 2012) y (Amatriain 2015) al final de la página.

4.1.5 ¿Algún consejo para la práctica?

Depende de los datos, pero es común encontrar ejemplos como 10 fold CV, más repetición: 10 fold CV, repeated 5 times. Otras veces nos encontramos con: 5 fold CV, repeated 3 times.

Y usando el promedio de la métrica deseada. También es recomendable usar el ROC porque está menos sesgado a las variables objetivo desequilibradas.

Dado que estas técnicas de validación consumen mucho tiempo, consideren la posibilidad de elegir un modelo que se ejecute rápidamente, permitiendo el ajuste del modelo, probando diferentes configuraciones, probando diferentes variables en “poco” tiempo. Los random forests son una excelente opción que da resultados rápidos y precisos. Más información sobre el rendimiento general de los bosques aleatorios en (Fernandez-Delgado 2014).

Otra buena opción son las gradient boosting machines, tienen más parámetros para ajustar que los random forests, pero al menos en R su implementación funciona rápido.

4.1.5.1 Volviendo al sesgo y la varianza

Los random forests se enfocan en disminuir el sesgo, mientras que…
Las gradient boosting machines se enfocan en minimizar la varianza. Hay más información en “Gradient boosting machine vs random forest” (stats.stackexchange.com 2015).

4.1.6 No se olviden: Preparación de los datos

Ajustar los datos de entrada transformándolos y limpiándolos tendrá un impacto en la calidad del modelo. A veces más que optimizar el modelo a través de sus parámetros.

Expandan este punto con el capítulo Preparación de datos.

4.1.7 Reflexiones finales

Validar los modelos mediante el remuestreo / la validación cruzada nos ayuda a estimar el error “real” que existe en los datos. Si el modelo se ejecuta en el futuro, ese es el error que se espera que tenga.
Otra ventaja es el ajuste del modelo, evitando el sobreajuste al seleccionar los mejores parámetros para un determinado modelo, Ejemplo en caret. El equivalente en Python está incluido en Scikit Learn.
La mejor prueba es la que hagan ustedes, adaptada a sus datos y necesidades. Prueben diferentes modelos y analicen el equilibrio entre el consumo de tiempo y cualquier métrica de precisión.

Estas técnicas de remuestreo podrían estar entre las poderosas herramientas detrás de sitios como stackoverflow.com o el software colaborativo de código abierto. Tener muchas opiniones para producir una solución menos sesgada.

Pero cada opinión debe ser confiable, imaginen pedirle un diagnóstico a diferentes médicos.

4.1.8 Lecturas adicionales

Tutorial: Cross validation for predictive analytics using R
Tutorial por Max Kahn (creador de caret): Comparing Different Species of Cross-Validation
El enfoque de validación cruzada también se puede aplicar a los modelos dependientes del tiempo, consulten el otro capítulo: Validación out-of-time.

4.2 Validación out-of-time

4.2.1 ¿De qué se trata esto?

Una vez que hemos construido un modelo predictivo, ¿qué tan seguros estamos de que capturó los patrones generales y no sólo los datos que ha visto (sobreajuste)?

¿Funcionará bien cuando esté en producción / en vivo? ¿Cuál es el error esperado?

4.2.2 ¿Qué tipo de datos?

Si los datos son generados a lo largo del tiempo y -digamos- todos los días tenemos nuevos casos como “visitas en un sitio web”, o “nuevos pacientes que llegan a un centro médico”, una validación robusta es la del enfoque Fuera de tiempo.

4.2.3 Ejemplo de Validación Fuera de tiempo

¿Cómo se hace?

Imaginen que estamos construyendo el modelo un Jan-01, entonces para construirlo usamos todos los datos hasta Oct-31. Entre estas fechas hay 2 meses.

Al predecir una variable binaria/de dos clases (o multiclase), es bastante senscillo: con el modelo que construimos -con datos <= Oct-31- le asignamos un score (probabilidad) en ese día exacto, y después medimos cómo los usuarios/pacientes/personas/casos evolucionaron durante esos dos meses.

Dado que el resultado de un modelo binario debería ser un número que indique la probabilidad de cada caso de pertenecer a una determinada clase (capítulo de Scoring de datos, probamos lo que el modelo “dijo” el “Oct-31” contra lo que realmente pasó el “Jan-01”.

El siguiente flujo de trabajo de validación puede resultarles útil a la hora de construir un modelo predictivo que implique tiempo.

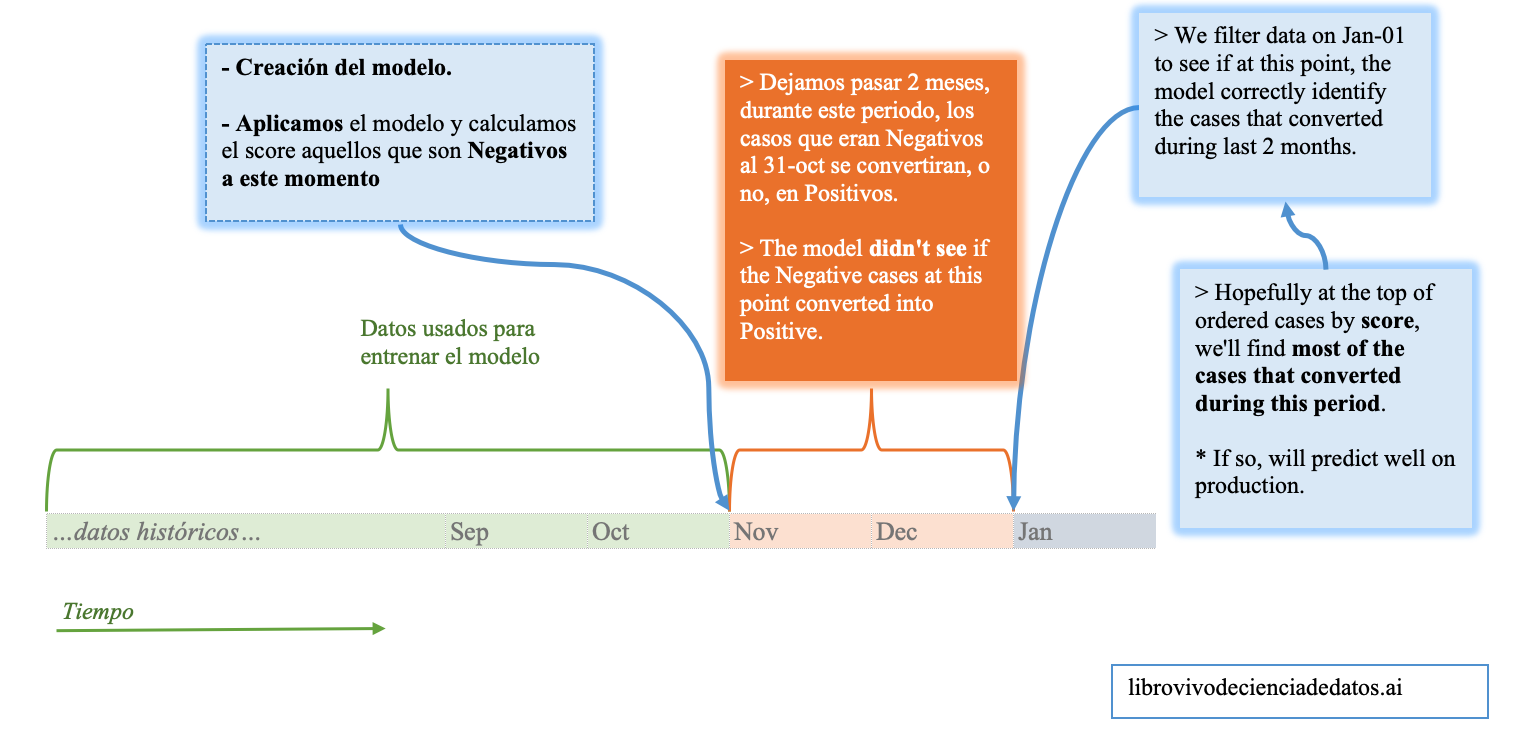
Figure 4.6: Un flujo de trabajo de validación para problemas que dependen del tiempo

Ampliar imagen.

4.2.4 Usando el análisis de Ganancia y Lift

Este análisis está explicado en otro capítulo (Ganancia y Lift) y se puede utilizar después de la validación fuera de tiempo.

Conservando solamente aquellos casos que fueron negative en Oct-31, obtenemos el score que devolvió el modelo en esa fecha, y la variable target es el valor que esos casos tuvieron en Jan-1.

4.2.5 ¿Qué pasa si la variable objetivo es numérica?

Ahora el sentido común y la necesidad del negocio están más presentes. Un resultado numérico puede tomar cualquier valor, puede aumentar o disminuir con el tiempo, por lo que puede que tengamos que considerar estos dos escenarios para ayudarnos a pensar en lo que consideramos éxito. Tal es el caso de la regresión lineal.

Escenario de ejemplo: Medimos el uso de alguna app (como la de homebanking), lo estándar sería que con el correr de los días los usuarios la utilizen más.

Ejemplos:

Predecir la concentración de una determinada sustancia en la sangre.
Predecir visitas en una página web.
Análisis de series temporales.

En estos casos también tenemos la diferencia entre: “lo que se esperaba” vs. “lo que es”.

Esta diferencia puede tomar cualquier valor. A este valor lo llamamos error o residuos.

Figure 4.7: Predicción y análisis del error

Si el modelo es bueno, este error debería ser ruido blanco, hay más información sobre esto en la sección “Análisis y regresión de series temporales” en (Wikipedia 2017 d). Sigue una curva normal cuando se cumplen algunas propiedades lógicas:

El error debería estar cerca de 0 -el modelo deberá tender su error a 0-.
El desvío estándar de este error debe ser finito -para evitar valores atípicos impredecibles-.
No tiene que haber una correlación entre los errores.
Distribución normal: esperen la mayoría de los errores cerca de 0, con los errores más grandes en una proporción menor a medida que el error aumenta -la probabilidad de encontrar errores más grandes disminuye exponencialmente-.

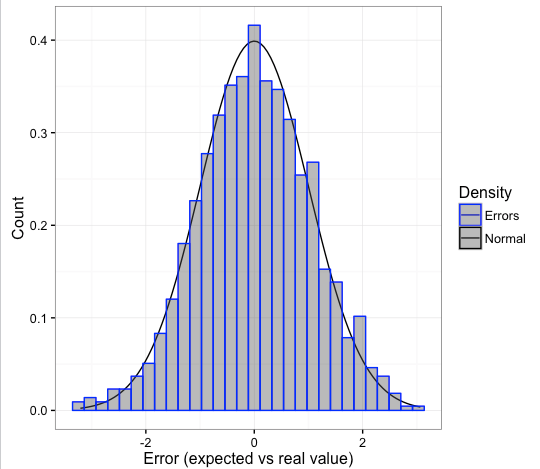
Figure 4.8: Una bella curva de error (distribución normal)

4.2.6 Reflexiones finales

La Validación fuera de tiempo es una poderosa herramienta de validación para simular la ejecución de un modelo en producción con datos que pueden no necesitar ni depender del muestreo.
El análisis del error es un capítulo importante en la ciencia de datos. Es hora de pasar al próximo capítulo, que intentará cubrir los conceptos clave de este tema: Conociendo el error.

4.3 Análisis de Ganancia y Lift

4.3.1 ¿De qué se trata esto?

Ambas métricas son extremadamente útiles para validar la calidad del modelo predictivo (resultado binario). Hay más información en Scoring de datos

Asegúrense de tener la última versión de funModeling (>= 1.3).

# Cargar funModeling
library(funModeling)

# Crear un modelo GLM 
fit_glm=glm(has_heart_disease ~ age + oldpeak, data=heart_disease, family = binomial)

# Obtener los scores/probabilidades de cada fila
heart_disease$score=predict(fit_glm, newdata=heart_disease, type='response')

# Graficar la curva de ganancia y lift
gain_lift(data=heart_disease, score='score', target='has_heart_disease')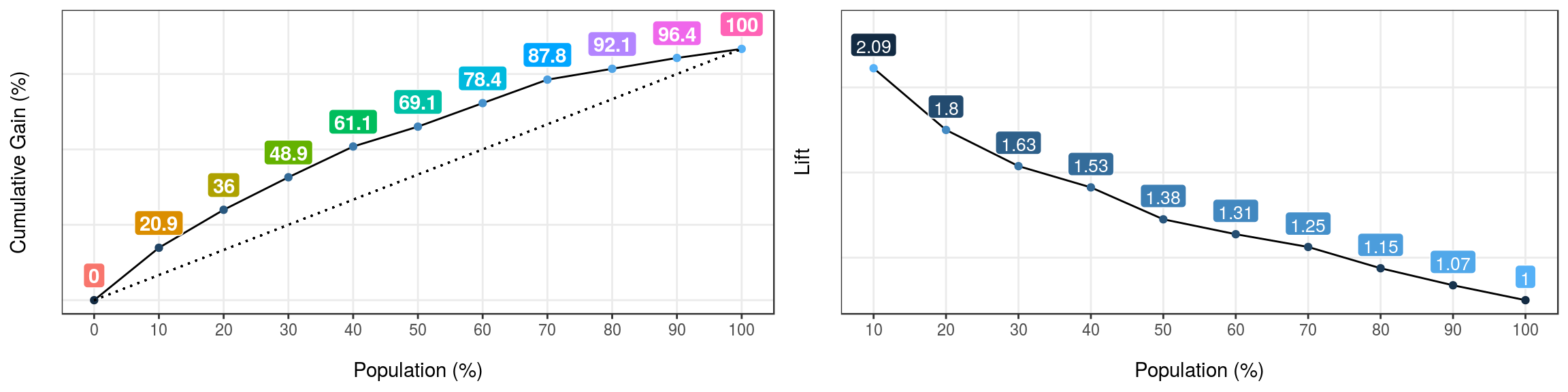

Figure 4.9: Curvas de ganancia y lift

##    Population   Gain Lift Score.Point
## 1          10  20.86 2.09   0.8185793
## 2          20  35.97 1.80   0.6967124
## 3          30  48.92 1.63   0.5657817
## 4          40  61.15 1.53   0.4901940
## 5          50  69.06 1.38   0.4033640
## 6          60  78.42 1.31   0.3344170
## 7          70  87.77 1.25   0.2939878
## 8          80  92.09 1.15   0.2473671
## 9          90  96.40 1.07   0.1980453
## 10        100 100.00 1.00   0.1195511

4.3.2 ¿Cómo interpretarlo?

Primero, cada caso está ordenado de acuerdo a la probabilidad de ser la clase menos representativa, es decir, según el valor de la puntuación.

Luego, la columna Gain acumula la clase positiva, por cada 10% de filas - columna Population.

Entonces el análisis de la primera fila sería:

“El primer 10 por ciento de la población, ordenado por score, acumula el 20.86% del total de casos positivos”

Por ejemplo, si estamos enviando e-mails basándonos en este modelo, y tenemos presupuesto para contactar solamente al 20% de nuestros usuarios, ¿cuántas respuestas esperamos recibir? Respuesta: 35.97%

4.3.3 ¿Qué pasa si no usamos un modelo?

Si no usamos un modelo, y seleccionamos un 20% aleatoriamente, ¿cuántos usuarios tenemos que contactar? Bueno, 20%. Ese es el significado de la línea punteada, que empieza en 0% y termina en 100%. Con un poco de suerte, usando el modelo predictivo le vamos a ganar a la aleatoriedad.

La columna Lift representa la proporción entre Gain y la ganancia por azar. Tomando como ejemplo la Población=20%, el modelo es 1.8 veces mejor que la aleatoriedad.

4.3.3.1 Usando el punto de corte ✂️

¿Qué valor del score alcanza el 30% de la población? Respuesta: 0.56

El punto de corte nos permite segmentar los datos.

4.3.3.2 Comparando modelos

En un buen modelo, la ganancia alcanzará el 100% “al principio” de la población, representando que separa las clases.

Al comparar modelos, una métrica rápida es ver si la ganancia al principio de la población (10-30%) es mayor.

Como resultado, el modelo con una mayor ganancia al principio habrá capturado más información de los datos.

Vamos a ilustrarlo….

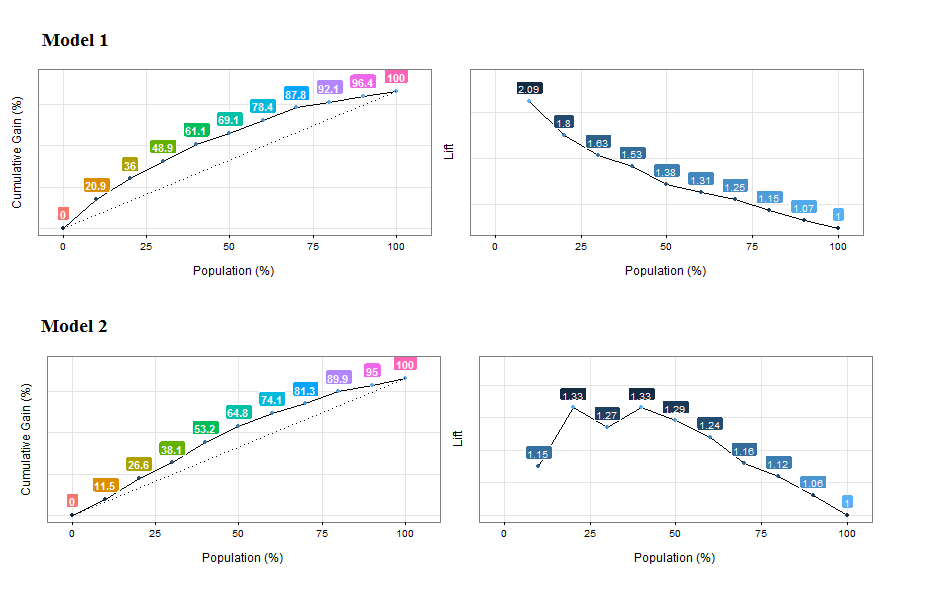
Figure 4.10: Comparando las curvas de ganancia y lift de dos modelos

Agrandar imagen.

Análisis de la ganancia acumulada: Model 1 alcanza el ~20% de casos positivos cerca del 10% de la población, mientras que Model 2 alcanza una proporción similar cerca del 20% de la población. Model 1 es mejor.

Análisis de lift: Lo mismo que antes, pero también resulta sospechoso que no todos los números de lift siguen un patrón descendiente. Quizás el modelo no está ordenando los primeros percentiles de la población. Los mismos conceptos de orden que vimos en el capítulo Análisis numérico de la variable objetivo usando cross_plot.

4.4 Scoring de datos

4.4.1 La intuición detrás

Los eventos pueden ocurrir, o no… aunque no tenemos el diario del lunes📰, podemos hacer una buena suposición de cómo va a ser.

El futuro está indudablemente ligado a la incertidumbre, y esta incertidumbre puede ser estimada.

4.4.1.1 Y hay diferentes objetivos…

Por ahora, este libro va a tratar el clásico: objetivo de Yes/No -también conocido como predicción binaria o multiclase.

Entonces, esta estimación es el valor de verdad de que un evento suceda, por lo que es un valor probabilístico entre 0 y 1.

4.4.1.2 Resultados de dos categorías vs. multi-categoría

Por favor tengan en cuenta que este capítulo fue escrito para un resultado binario (dos categorías), pero un objetivo multi-categoría puede tomarse como un enfoque general de una clase binaria.

Por ejemplo, al tener una variable objetivo con 4 valores diferentes, puede haber 4 modelos que predicen la probabilidad de pertenecer a una determinada clase, o no. Y luego un modelo superior que tome los resultados de esos 4 modelos y prediga la clase final.

4.4.1.3 ¡¿Qué dijo?! 😯

Algunos ejemplos: - ¿Este cliente va a comprar este producto? - ¿Este paciente va a mejorar? - ¿Cierto evento va a ocurrir en las próximas semanas?

Las respuestas a estas preguntas son Verdadero o Falso, pero la esencia es tener un score, o un número que indique la probabilidad de que ocurra un determinado evento.

4.4.1.4 Pero necesitamos más control…

Muchos recursos de machine learning muestran la versión simplificada -que es un buena para empezar- obteniendo la clase final como resultado. Digamos:

Enfoque simplificado:

Pregunta: ¿Esta persona va a tener una enfermedad cardíaca?
Respuesta: “No”

Pero hay algo antes de la respuesta “Sí/No”, y eso es el score:

Pregunta: ¿Cuál es la probabilidad de que esta persona tenga una enfermedad cardíaca?
Respuesta: “25%”

Entonces primero obtenemos el puntaje, y luego, de acuerdo a nuestras necesidades, definimos el punto de corte. Y esto es muy importante.

4.4.2 Veamos un ejemplo

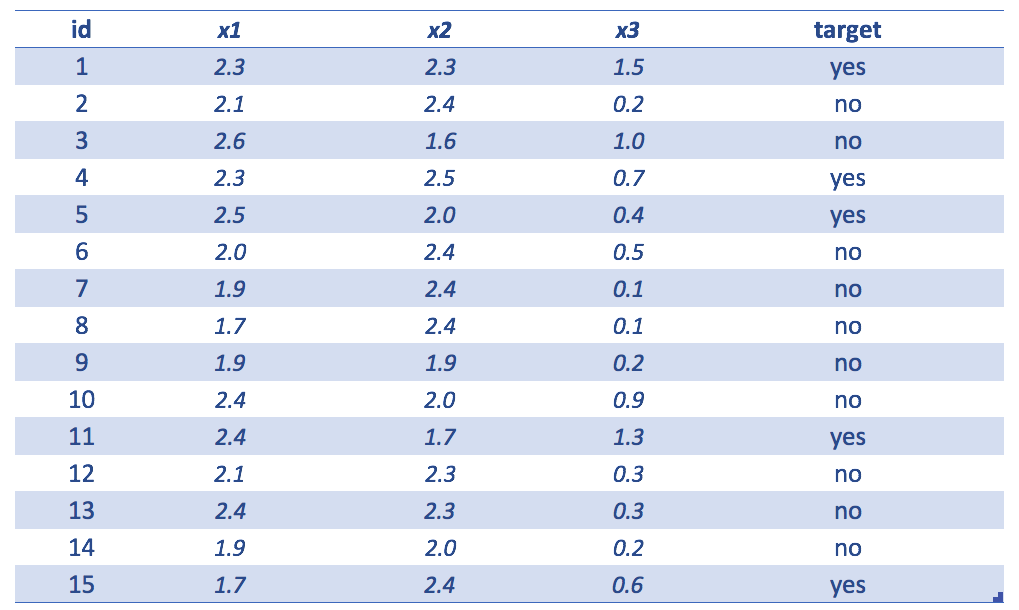
Figure 4.11: Ejemplo simple con un conjunto de datos

La tabla del ejemplo muestra lo siguiente

id=identidad
x1,x2 y x3 variables de entrada
target=variable a predecir

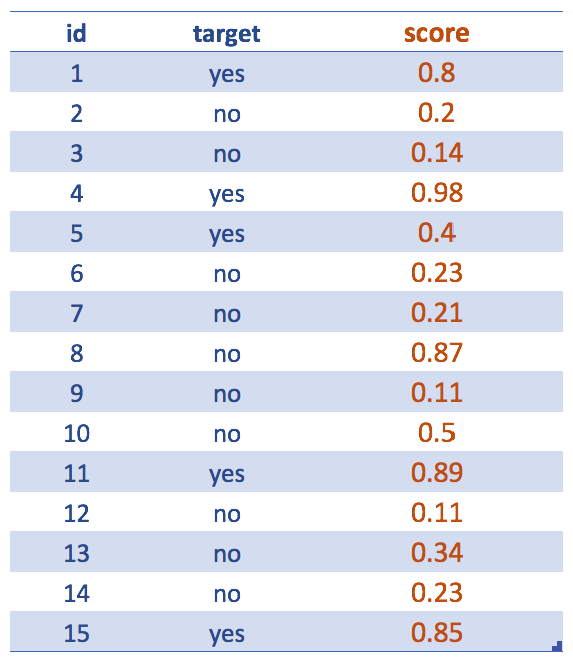
Figure 4.12: Obteniendo el score (resultado del modelo predictivo)

Dejando de lado la variables de entrada… Después de crear el modelo predictivo, como un modelo de random forest, nos interesan los scores. Aunque nuestro objetivo final es llegar a una variable predicha de yes/no.

Por ejemplo, las siguientes 2 oraciones expresan lo mismo: La probabilidad de que sea yes es 0.8 <=> La probabilidad de que sea no es 0.2.

Tal vez ya se entendió, pero el score generalmente se refiere a la clase menos representativa: yes.

✋ Sintaxis en R -salteen esta sección si no quieren ver código-

La siguiente oración devolverá el score:

score = predict(randomForestModel, data, type = "prob")[, 2]

Por favor tengan en cuenta que en otros modelos esta sintaxis puede variar un poco, pero el concepto será el mismo. Incluso en otros lenguajes de programación.

Donde prob indica que queremos las probabilidades (o scores).

La función predict + el parámetro type="prob" devuelve una matriz de 15 filas y 2 columnas: la primera indica la probabilidad de que sea no mientras la segunda columna muestra lo mismo para la clase yes.

Dado que la variable objetivo puede ser no o yes, entonces [, 2] devuelve la probabilidad de que sea -en este caso- yes (que es el complemento de la probabilidad de no).

4.4.3 Todo se trata del punto de corte 📏

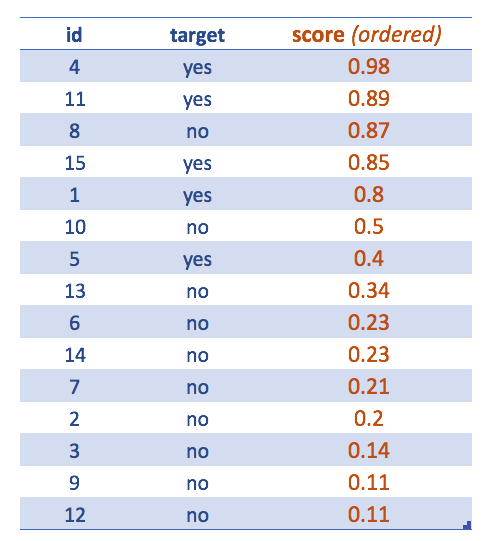
Figure 4.13: Casos ordenados por score más alto

Ahora la tabla está ordenada por score descendiente.

Esto sirve para ver cómo extraer la clase final teniendo por defecto el punto de corte en 0.5. Ajustar el punto de corte conducirá a una mejor clasificación.

Las métricas de precisión o la matriz de confusión siempre están asociadas a un determinado valor del punto de corte.

Después de asignar el punto de corte, podemos ver los resultados de la clasificación obteniendo los famosos:

✅ Verdadero Positivo (VP): Es verdad que la clasificación es positiva, o, “el modelo le acertó a la clase positiva (yes)”.
✅ Verdadero Negativo (VN): Lo mismo que antes, pero con la clase negativa (no).
❌ Falso Positivo (FP): Es falso que la clasificación es positiva, o, “el modelo falló, predijo yes pero el resultado fue no”
❌ Falso Negativo (FN): Lo mismo que antes, pero con la clase negativa, “el modelo predijo un resultado negativo, pero fue positivo”, o, “el modelo predijo no, pero la clase fue yes”

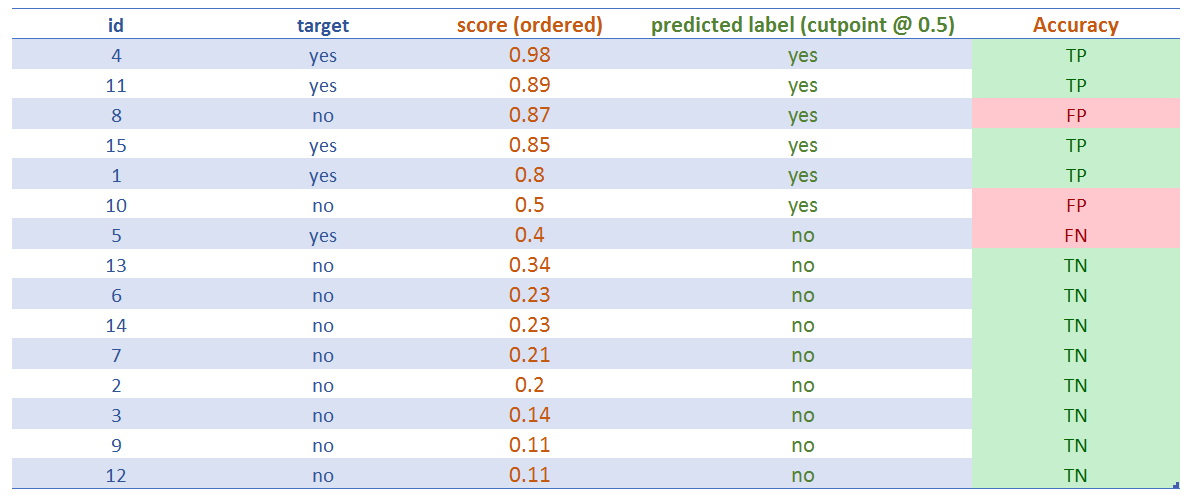
Figure 4.14: Asignar la categoría predicha (cutoff=0.5)

4.4.4 El mejor y peor escenario

Al igual que la filosofía Zen, el análisis de los extremos nos ayudará a encontrar el punto medio.

👍 El mejor escenario es aquel en el que las tasas de VP y VN son 100%. Eso significa que el modelo predice correctamente todos los yes y todos los no; (como resultado, las tasas de FP y FN son 0%).

¡Pero esperen ✋! Si encontramos una clasificación perfecta, ¡probablemente se deba a un sobreajuste!

👎 El peor escenario -lo opuesto al último ejemplo- es aquel en el que las tasas de FP y FN son 100%. Ni siquiera la aleatoriedad puede lograr un escenario tan horrible.

¿Por qué? Si las clases están balanceadas, 50/50, al tirar una moneda acertaremos alrededor de la mitad de los resultados. Esta es la línea de base común para probar si el modelo es mejor que la aleatoriedad.

En el ejemplo provisto, la distribución de clases es 5 para yes, y 10 para no; entonces: 33,3% (5/15) es yes.

4.4.5 Comparar clasificadores

4.4.5.1 Comparar resultados de clasificación

❓ Trivia: Si un modelo predice correctamente este 33.3% (Tasa de VP=100%), ¿es un buen modelo?

Respuesta: Depende de cuántos ‘yes’ predijo el modelo.

Un clasificador que siempre predice yes, tendrá una tasa de VP de 100%, pero es absolutamente inútil dado que muchos de esos yes en realidad serán no. De hecho, la tasa de FP será alta.

4.4.5.2 Comparar la etiqueta de orden basándonos en el score

Un clasificador debe ser confiable, y esto es lo que mide la curva ROC al trazar las tasas de VP vs FP. Cuanto mayor sea la proporción de VP sobre FP, mayor será el área debajo de la curva ROC (AUC por Area Under Curve, en inglés).

La intuición detrás de la curva ROC es obtener una medida de sanidad con respecto al score: qué tan bien ordena la etiqueta. Idealmente, todas las etiquetas positivas deben estar en la parte superior y las negativas en la parte inferior.

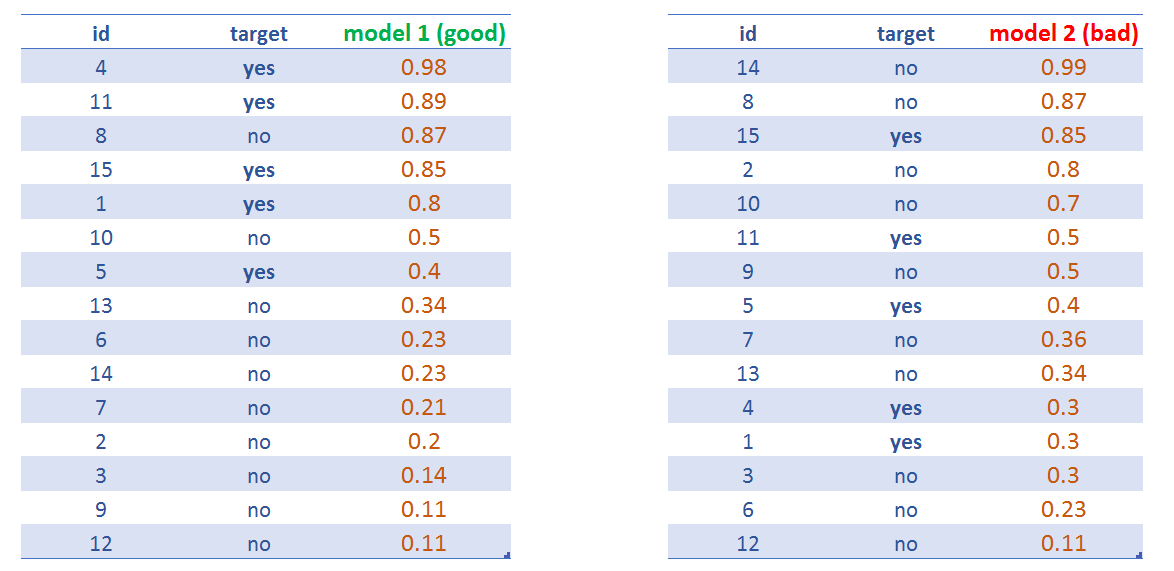
Figure 4.15: Comparar scores de dos modelos predictivos

model 1 tendrá una AUC mayor que model 2.

En Wikipedia hay artículo bueno y exhaustivo sobre este tema (en inglés): https://en.wikipedia.org/wiki/Receiver_operating_characteristic

Está la comparación de los 4 modelos, con el punto de corte en 0.5:

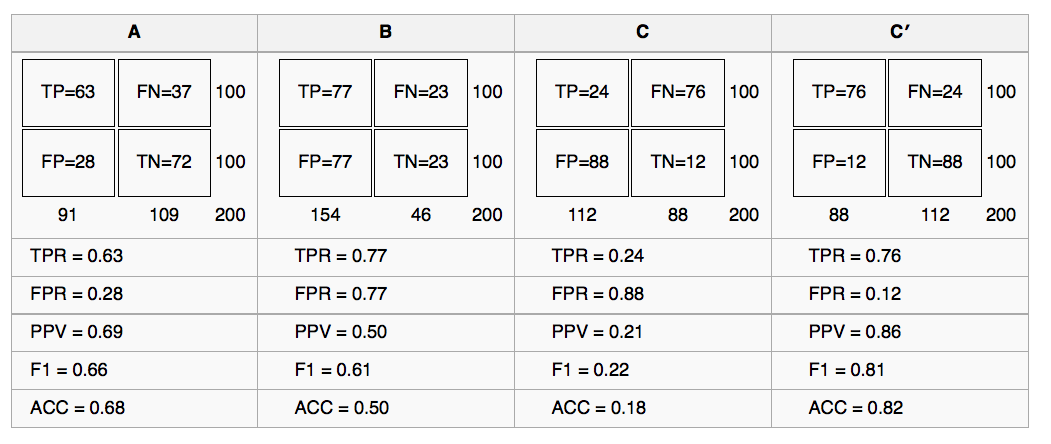
Figure 4.16: Comparando 4 modelos predictivos

4.4.6 ¡Manos a la obra en R!

Analizaremos tres escenarios basándonos en diferentes puntos de corte.

# install.packages("rpivotTable") 
# rpivotTable: crea una tabla pivote dinámicamente, también permite graficar, más información en: https://github.com/smartinsightsfromdata/rpivotTable

library(rpivotTable)

## Leer los datos
data=read.delim(file="https://goo.gl/ac5AkG", sep="\t", header = T, stringsAsFactors=F)

4.4.6.1 Escenario 1: punto de corte @ `0.5`

Matriz de confusión clásica, indica cuántos casos caen en la intersección de valor real vs. predicho:

data$predicted_target=ifelse(data$score>=0.5, "yes", "no")

rpivotTable(data = data, rows = "predicted_target", cols="target", aggregatorName = "Count", rendererName = "Table", width="100%", height="400px")

Figure 4.17: Matriz de confusión (métrica: conteo)

Otra vista, ahora cada columna suma 100%. Es bueno responder las siguientes preguntas:

rpivotTable(data = data, rows = "predicted_target", cols="target", aggregatorName = "Count as Fraction of Columns", rendererName = "Table", width="100%", height="400px")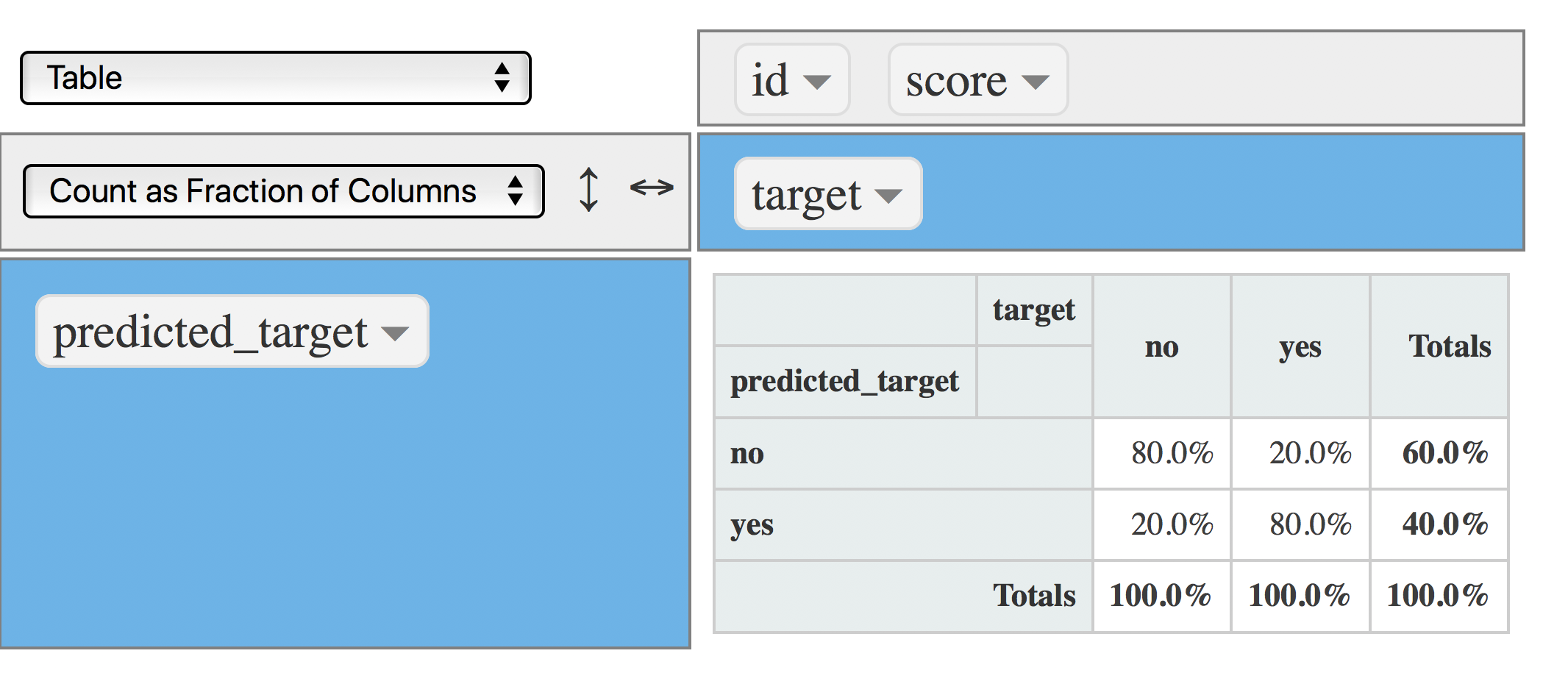

Figure 4.18: Matriz de confusión (punto de corte en 0.5)

¿Cuál es el porcentaje de valores yes reales capturados por el modelo? Respuesta: 80% También conocido como Precisión (PPV por Positive Predictive Value en inglés)
¿Cuál es el procentaje de yes que arrojó el modelo? 40%.

Entonces, a partir de estas dos oraciones:

El modelo clasifica 4 de cada 10 predicciones como yes, y en este segmento -el yes- acierta en un 80%.

Otra vista: el modelo acierta 3 casos de cada 10 predicciones de yes (0.4/0.8=3.2, o 3, redondeando para abajo).

Nota: La última forma de análisis se puede encontrar cuando se construyen las reglas de una asociación (análisis de afinidad o de cesta de la compra), y un modelo de árbol de decisión.

4.4.6.2 Escenario 2: punto de corte @ `0.4`

Hora de cambiar el punto de corte a 0.4, la cantidad de yes será mayor:

data$predicted_target=ifelse(data$score>=0.4, "yes", "no")

rpivotTable(data = data, rows = "predicted_target", cols="target", aggregatorName = "Count as Fraction of Columns", rendererName = "Table", width="100%", height="400px")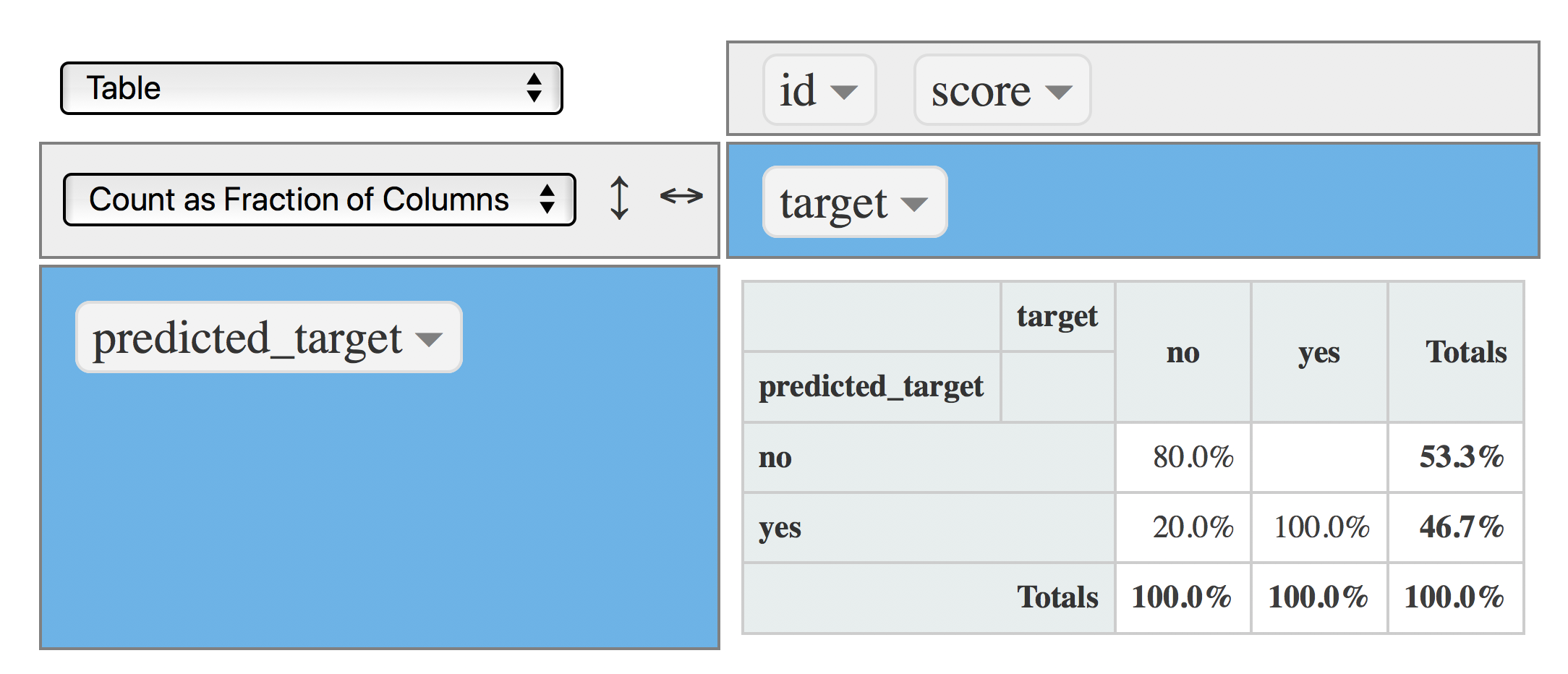

Figure 4.19: Matriz de confusión (punto de corte en 0.4)

Ahora el modelo captura el 100% de los yes (VP), por lo que la cantidad total de yes producida por el modelo aumentó a 46.7%, pero sin ningún costo, dado que los VN y FP permanecieron iguales 👍 .

4.4.6.3 Escenario 3: punto de corte @ `0.8`

¿Quieren disminuir la tasa de FP? Configuren el punto de corte en un valor superior, por ejemplo: 0.8, que causará que disminuya la cantidad de yes producida por el modelo:

data$predicted_target=ifelse(data$score>=0.8, "yes", "no")

rpivotTable(data = data, rows = "predicted_target", cols="target", aggregatorName = "Count as Fraction of Columns", rendererName = "Table", width="100%", height="400px")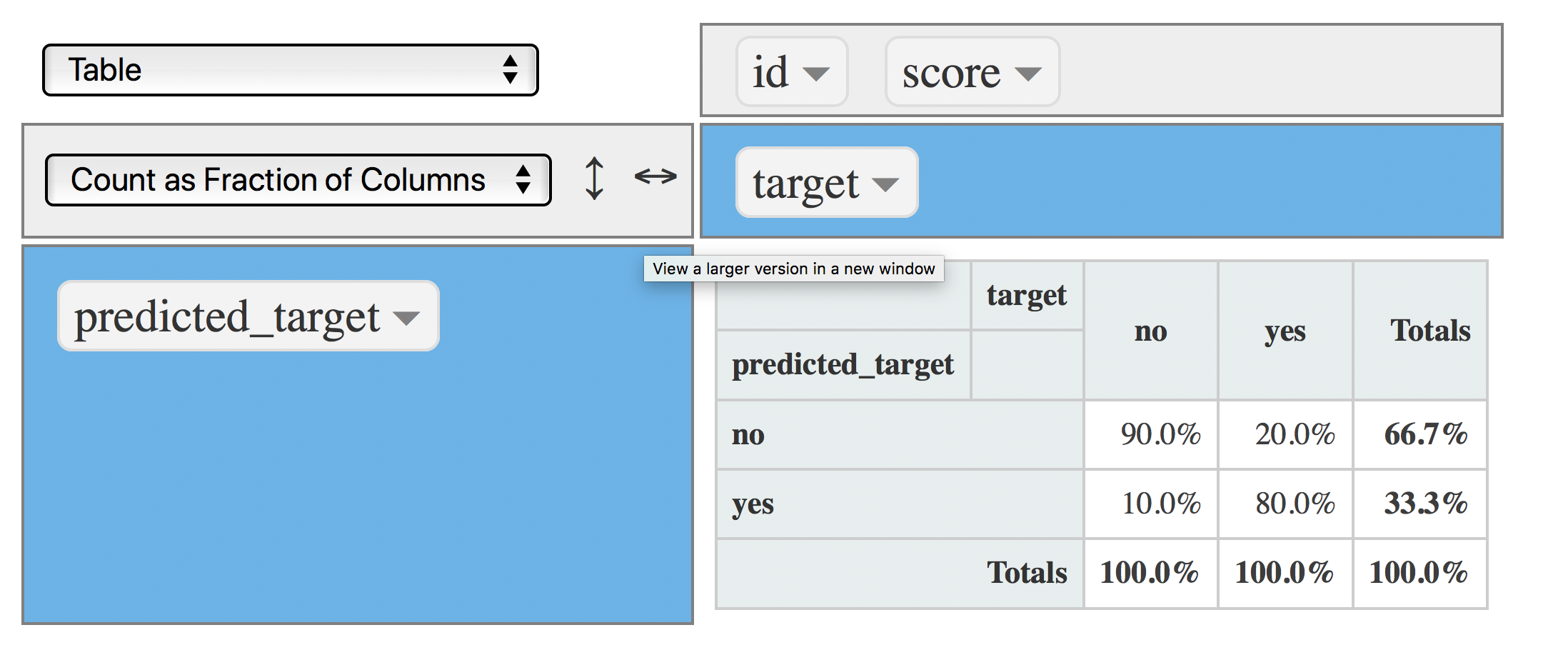

Figure 4.20: Matriz de confusión (punto de corte en 0.8)

Ahora la tasa de FP disminuyó a 10% (de 20%), y el modelo aún captura el 80% de VP que es la misma tasa que la que obtuvimos con el punto de corte en 0.5 👍 .

Disminuir el punto de corte a 0.8 mejoró el modelo sin costo alguno.

4.4.7 Conclusiones

Este capítulo se ha centrado en la esencia de la predicción de una variable binaria: Para producir un score o número de probabilidad que ordena la variable objetivo.
Un modelo predictivo mapea la entrada con la salida.
No hay un único y mejor valor de punto de corte, depende de las necesidades del proyecto, y está limitado por la tasa de Falso Positivo y Falso Negativo que podemos aceptar.

Este libro trata aspectos generales sobre el desempeño de los modelos en el capítulo Conociendo el error

Referencias

Raschka, Sebastian. 2017. “Machine Learning Faq.” http://sebastianraschka.com/faq/docs/evaluate-a-model.html.

Hyndman, Rob J. 2010. “Why Every Statistician Should Know About Cross-Validation?” https://robjhyndman.com/hyndsight/crossvalidation/.

Amatriain, Xavier. 2015. “In Machine Learning, What Is Better: More Data or Better Algorithms.” http://www.kdnuggets.com/2015/06/machine-learning-more-data-better-algorithms.html.

Fortmann, Scott. 2012. “Understanding the Bias-Variance Tradeoff.” http://scott.fortmann-roe.com/docs/BiasVariance.html.

Hyndman, Rob J. 2017. “ARIMA Modelling in R.” https://www.otexts.org/fpp/8/.

Fernandez-Delgado, Manuel. 2014. “Do We Need Hundreds of Classifiers to Solve Real World Classification Problems?” http://jmlr.csail.mit.edu/papers/volume15/delgado14a/delgado14a.pdf.

stats.stackexchange.com. 2015. “Gradient Boosting Machine Vs Random Forest.” https://stats.stackexchange.com/questions/173390/gradient-boosting-tree-vs-random-forest.

Wikipedia. 2017d. “White Noise - Time Series Analysis and Regression.” https://en.wikipedia.org/wiki/White_noise.